
May 1997
Active Control of Whirl Motions
GG Spacecraft and PGB
Control Law A : Sequential Derivative
Relative velocity of bodies is computed by taking differences of successive
Measurements from the rotating displacement sensors
Control Law B: B1 Derivative with Tspin (
0.2 s) step
Relative velocity is computed by taking differences of measurements
Taken by the rotating displacement sensors 1 spin period apart
B2: B1 + Averaging of Relative Velocity over 10Tspin (
2 s)
B3: B1 + B2 + Filter (Best Fit) over 1 T
whirl ~ 300 s
Results of Simulations with the DCAP Code of Alenia Spazio
Control Law A Þ (Applied in estec Report on GG)
Control force applied/passive elastic force (of ideal control case)~ 2x103 !
The slow relative velocity of the whirl motion is NOT recovered ;
the measured relative velocity is dominated by the (large) velocity of spin
of the measurement sensors;
The system is ENTIRELY DOMINATED by the active control forces
Control Law A is not Adequate to the GG System
Control Law B: B1Þ
Control force applied smaller than in case of Control Law A by a factor 10
B2Þ
Control force smaller than in case of Control Law A by a factor 100B3Þ
Control force smaller than in case of Control Law A by a factor 2000
And close to theoretical value OK !
Controlled system reaches stationary state after 8,000 s (Orbital period = 5,700 s)
At stationary state the whirl radius is maintained within the sensitivity of the sensors
Which measure relative displacements (10-8 m)
Control law A (Applied in estec Report on GG)

Figure A-1
. Relative displacements (X and Y components, in units of m m) of the centres of mass of two spinning bodies (GG outer spacecraft and the PGB) as measured by capacitance sensors with sensitivity s =10-2 m m and rotating with the bodies. The displacements are given as functions of time for 8,000 s. The Y axis is pointed to the centre of the Earth, hence the largest effect of the residual atmospheric drag (which acts on the outer surface of the spacecraft but not directly on the PGB laboratory suspended inside it) is a constant displacement along the X axis (of ~ 0.08 m m); the second harmonic (40% of it) appears in this system as a variation at the orbital period (5,700 s). The short period variations (at the whirl/natural period of ~ 300 s) are those due to the whirl instability whose amplitude will grow unless it is actively controlled. The dashed curve shows the state of the system if the whirl motion had been perfectly damped. Here the system is controlled actively (with Control Law A, the one used by ESTEC) but clearly the stationary state is not reached.
Control Law A (Applied in estec Report on GG)
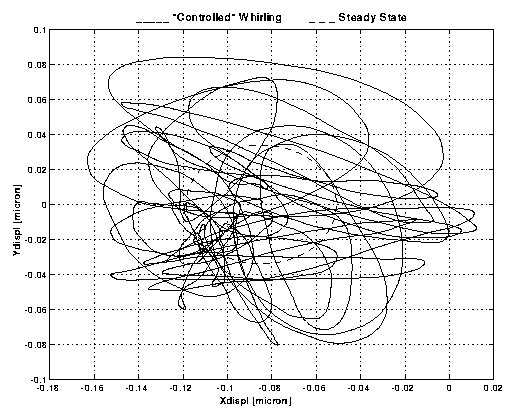
Figure A-2
. Polar plot of the X and Y displacements shown in Figure A-1. It shows the trajectory of the relative motion of the two bodies. The dashed curve shows the stationary state that the system would reach if the whirl motion had been perfectly damped. The "control" forces do not bring the system to the stationary state and become instead the dominant forces.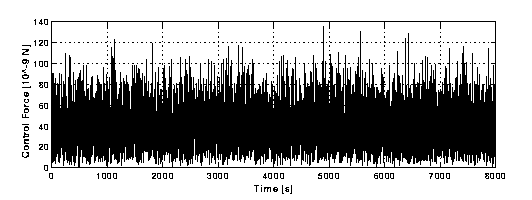
Figure A-3
. "Control" force (as function of time) which acts in Figures A-1 and A-2 above. Its average value is about 2,000 times larger than the passive elastic force between the bodies if their whirl motion were properly controlled to the level of sensitivity of the displacement sensors (s =10-2 m m). In this system the elastic forces are larger because the active "control" forces cause large displacements (see Figures A-1 and A-2). "Control" Law A, which produces Figures A-1,A-2 and A-3 is clearly not adequate for the GG system, which instead should be dominated by the small, passive elastic forces.Control Law B1
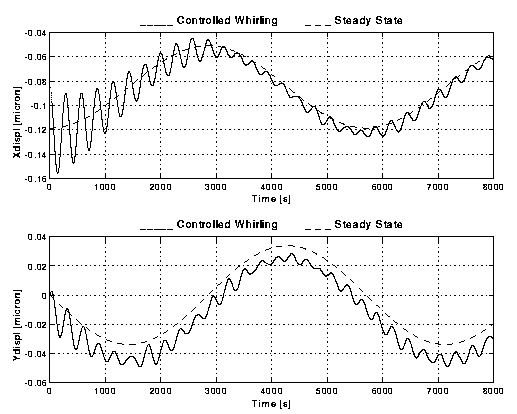
Figure B1-1
. Relative displacements (X and Y components, in units of m m) of the centres of mass of two spinning bodies (GG outer spacecraft and the PGB) as measured by capacitance sensors with sensitivity s =10-2 m m and rotating with the bodies. The displacements are given as functions of time for 8,000 s. The Y axis is pointed to the centre of the Earth, hence the largest effect of the residual atmospheric drag (which acts on the outer surface of the spacecraft but not directly on the PGB laboratory suspended inside it) is a constant displacement along the X axis (of ~ 0.08 m m); the second harmonic (40% of it) appears in this system as a variation at the orbital period (5,700 s). The short period variations (at the whirl/natural period of ~ 300 s) are those due to the whirl instability whose amplitude will grow unless it is actively controlled. The dashed curve shows the state of the system if the whirl motion had been perfectly damped. Here the system is controlled actively with Control Law B1 (see page 1); the controlled system gets close to the stationary state but a bias remains, particularly in the Y component of the displacement.
Control Law B1
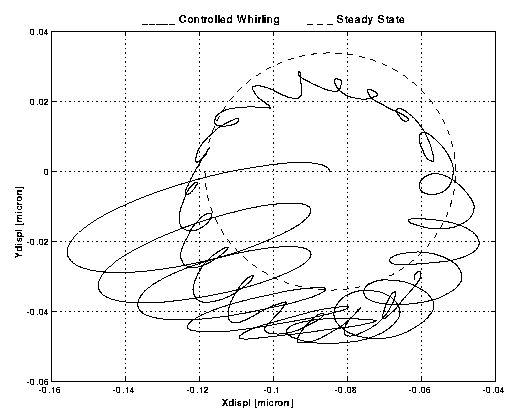
Figure B1-2
. Polar plot of the X and Y displacements shown in Figure B1-1. It shows the trajectory of the relative motion of the two bodies. The dashed curve shows the stationary state that the system would reach if the whirl motion had been perfectly damped. The control forces do not bring the system close enough to the stationary state.
Figure B1-3
. Control force (as function of time) which acts in Figures B1-1 and B1-2 above. Its average value is 10 times smaller than in Figure A-3, but still larger than the passive elastic force. Control Law B1, which produces Figures B1-1, B1-2 and B1-3 is not yet adequate for the GG system which should be dominated by the small, passive elastic forces.Control Law B2

Figure B2-1
. Relative displacements (X and Y components, in units of m m) of the centres of mass of two spinning bodies (GG outer spacecraft and the PGB) as measured by capacitance sensors with sensitivity s =10-2 m m and rotating with the bodies. The displacements are given as functions of time for 8,000 s. The Y axis is pointed to the centre of the Earth, hence the largest effect of the residual atmospheric drag (which acts on the outer surface of the spacecraft but not directly on the PGB laboratory suspended inside it) is a constant displacement along the X axis (of ~ 0.08 m m); the second harmonic (40% of it) appears in this system as a variation at the orbital period (5,700 s). The short period variations (at the whirl/natural period of ~ 300 s) are those due to the whirl instability whose amplitude will grow unless it is actively controlled.. The dashed curve shows the state of the system if the whirl motion had been perfectly damped. Here the system is controlled actively with Control Law B2 (see page 1); the controlled system gets closer to the stationary state than in Figure B1-1 and the bias observed there is reduced..Control Law B2
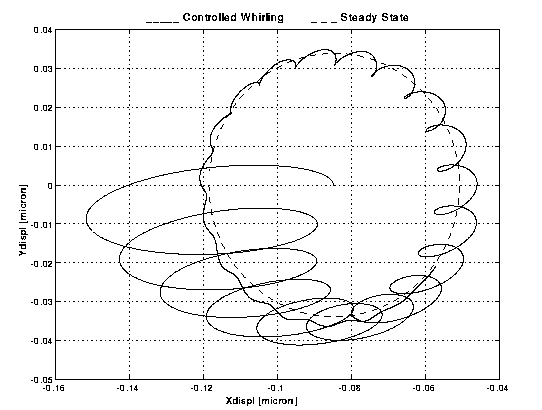
Figure B2-2
. Polar plot of the X and Y displacements shown in Figure B2-1. It shows the trajectory of the relative motion of the two bodies. The dashed curve shows the stationary state that the system would reach if the whirl motion had been perfectly damped. The control forces bring the system closer to the stationary state than in Figure B1-2.
Figure B2-3
. Control force (as function of time), which acts in Figures B2-1 and B2-2 above. Its average value is about 10 times smaller than in Figure B1-3, but still about 10 times larger than the passive elastic force. Control Law B2, which produces Figures B2-1, B2-2 and B2-3 is better than control law B1 but not yet adequate for the GG system which should be dominated by the small, passive elastic forces.
Control Law B3
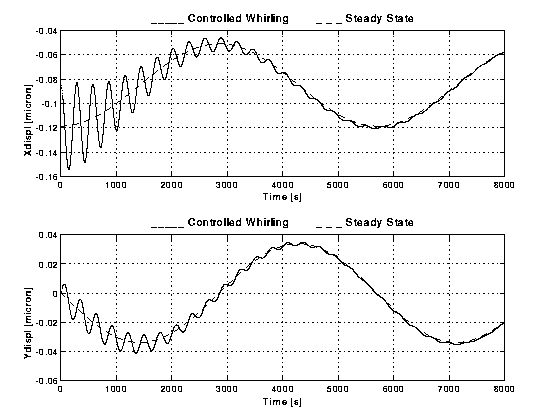
Figure B3-1. Relative displacements (X and Y components, in units of m m) of the centres of mass of two spinning bodies (GG outer spacecraft and the PGB) as measured by capacitance sensors with sensitivity s =10-2 m m and rotating with the bodies. The displacements are given as functions of time for 8,000 s. The Y axis is pointed to the centre of the Earth, hence the largest effect of the residual atmospheric drag (which acts on the outer surface of the spacecraft but not directly on the PGB laboratory suspended inside it) is a constant displacement along the X axis (of ~ 0.08 m m); the second harmonic of (40% of it) appears in this system as a variation at the orbital period (5,700 s). The short period variations (at the whirl/natural period of ~ 300 s) are those due to the whirl instability whose amplitude will grow unless it is actively controlled. The dashed curve shows the state of the system if the whirl motion had been perfectly damped.. Here the system is controlled actively with Control Law B3 (see page 1); after 8,000 s only (a little more than one orbital period of the spacecraft around the Earth) the controlled system reaches the stationary state as desired.
Control Law B3

Figure B3-2
.. Polar plot of the X and Y displacements shown in Figure B3-1. It shows the trajectory of the relative motion of the two bodies The dashed curve shows the stationary state that the system would reach if the whirl motion were perfectly damped. The control forces bring the system to its stationary state in 8,000 s only.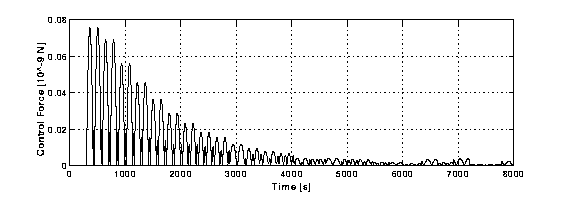
Figure B3-3. Control force (as function of time) applied in Figures B3-1 and B3-2 above. Its average value once the stationary state has been reached (after 8,000 s only) is smaller by more than a factor 2,000 than the value shown in Figure A-3 when Control Law A (the same as the one used in the ESTEC Report on GG) was applied. This value is about 1.2 times larger than the theoretical value of the destabilising force which must be damped, namely (1/Q) of the passive elastic force, with Q the quality factor of the system at the spin frequency (5 Hz). For the spacecraft/PGB suspension the Q measured experimentally is 90. This is the lowest Q value in the GG system and therefore the case shown here is the most difficult from the viewpoint of active control. Yet, it is apparent that it can be controlled by active forces as small as predicted theoretically, even though the capacitance sensors/actuators are rotating.
(Anna Nobili- nobili@dm.unipi.it)