GG: The Mission Goals and Its Novelty
1.1 The Scientific Objective
The scientific objective of the GALILEO GALILEI
(GG) small space mission is to test a fundamental "Principle'' of
modern Physics ---the EquivalencePrinciple (EP) formulated by Einstein
generalizing Galileo's and Newton's work--- to 1 part in 1017, 10 the best
ground experiments with laboratory bodies having found no violation to 1 part in 1012
(Roll, Krotkov and Dicke 1964; Braginsky and Panov 1972; Adelberger et al. 1990; Su et al.
1994). Nearly every student hears about Galileo's mass dropping experiment at school. No
image of science has captured the imagination of people more than the one of Galileo
dropping masses from the leaning tower of Pisa. Testing theUniversality of Free Fall,
that Galileo pioneered at the beginning of the 17th century, is indeed the most
direct experimental test of the Equivalence Principle , in fact
not a Principle but a basic property of gravitation, the
first discovered and yet most intriguing physical interaction. Unlike all other tests
of General Relativity , which check its consequences and
predictions, an experiment on the Equivalence Principle
tests the foundations of General Relativity and of all metric theories of gravity alike,
it probes the very essence of gravity and its uniqueness among the fundamental forces of
Nature. In the next decades a new physics might be developed that will overcome the
current, unsatisfactory framework: a high accuracy, unquestionable, experimental result on
the Equivalence Principle ---no matter whether
it is violated or confirmed--- will be a crucial asset for this new physics. And this is
how it has to be, because physics is an experimental science in which any theory, in spite
of its internal consistency and beauty, has to confront experiments, and ultimately will
stand or fall depending solely on experimental results. In his ``Discorsi
e dimostrazioni matematiche intorno a due nuove scienze... published in Leiden
in 1638 while he was blind and under house arrest in Italy, Galileo reported
results of experiments carried out almost forty years earlier with pendula and the
inclined plane. He formulated with astonishing neatness what lately became known as
the Universality of Free--Fall (on which
Einstein's Equivalence Principle was based), i.e. that
all bodies fall in the same way regardless of their mass and composition:
... ``veduto, dico questo, cascai in opinione che se si levasse
totalmente la resistenza del mezzo, tutte le materie descenderebbero con eguali velocita
'' ( ... ``having observed this I came to the conclusion that, if one could
totally remove the resistance of the medium, all substances would fall at equal speeds''
). About 80 years after Galileo's first experiments Newton went further,
actually recognizing the proportionality of mass and
weight . Newton regarded this proportionality as so important
that he devoted to it the opening paragraph of the Principia , where he
stated:``this quantity that I mean hereafter under the name of ... mass ... is known
by the weight ... for it is proportional to the weight as I have found by experiments on
pendulums, very accurately made... '' . At the beginning of the 20th
century, almost 300 years since Galileo's work, Einstein realized that because
of the proportionality between the gravitational (passive) mass mg and the
inertial mass mi, the effect of gravitation is locally equivalent to the effect
of an accelerated frame and can be locally cancelled: this is the Weak
Equivalence Principle . In a freely falling system all masses fall equally fast,
hence gravitational acceleration has no local dynamical effects. Einstein then generalized
this principle to the Strong Equivalence Principle , on which
he based his theory of General Relativity, so far the best theory of gravitation. The
Strong Equivalence Principle states that in an
electromagnetically shielded laboratory, freely falling and non rotating, the laws of
physics ---including their numerical content--- are independent of the location of the
laboratory. In such a laboratory all particles free of non gravitational forces move with
the same acceleration. Therefore, according to Einstein, the effects
of gravity are equivalent to the effects of living in a curved spacetime . In this
sense the weak equivalence principle expresses the very essence of General Relativity and
as such it deserves to be tested as accurately as possible. In the last 30
years since the advent of the space age General Relativity has been subject to extensive
experimental testing as never before in its first 50 years of existence, and
so far it has come out having no real competitors (see e.g. Will 1992); the crucial area
where experimental gravitation is likely to play an important role is in the verification
of the universality of free fall as a test of the weak equivalence principle itself, since
it is tantamount to testing whether gravitation can be ascribed to a metric structure of
spacetime. The total mass-energy of a body is the sum of many terms corresponding to the
energy of all the conceivable interactions and components: ![]() . For two bodies A and B of
different composition the Eotvos parameter
. For two bodies A and B of
different composition the Eotvos parameter ![]() can be generalized into
can be generalized into
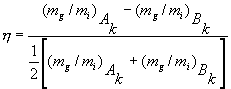
such that a non-zero value of h k would define the violation of equivalence between the inertial and gravitational mass- - energy of the k - th kind. For instance, the rest mass would contribute (as a fraction of the total) for ~1; the nuclear binding energy for 8× 10-3, the mass difference between neutron and proton for 8× 10-4(A-Z) ( A being the number of protons plus neutrons and Z the number of protons in the nucleus), the electrostatic energy of repulsion in the nuclei for 6× 10-4Z2A-4/3 , the mass of electrons for 5× 10-4Z, the antiparticles for ~ 10-7, the weak interactions responsible of b decay for ~ 10-11. From the point of view of conventional field theory, the verification of all these separate Equivalence Principles corresponds to a very peculiar coupling of each field to gravity; whether and why it should be so in all cases is a mystery. Let us consider the case of antiparticles. A peculiarity of gravity, strictly related to the Equivalence Principle , is that there is so far no evidence for antigravity , namely for the possibility that matter is gravitationally repelled by antimatter. A negative ratio of inertial to gravitational mass would obviously violate the Equivalence Principle and forbid any metric theory of gravity. Yet, there are theoretical formulations which would naturally lead to antigravity (Scherk 1979), and experiments have been proposed to directly explore the relation between gravity and antimatter. The idea was to make a Galileo--type mass dropping experiment using a proton and an antiproton in order to check whether they both fall like ordinary matter or not. The experiment was proposed to CERN by an international team of scientists (Beverini et al. 1986). Unfortunately, while experiments concerning the inertial mass of antiparticles have been highly successful, and these are very accurately known, gravitational experiments (i.e. involving the gravitational mass of antiparticles) are extremely difficult because of the far larger electric effects, such as those due to stray electric fields in the drift tube. Indeed, the latter have so far hindered the above mentioned experiment. In absence of such direct tests, an improvement by several orders of magnitude of current tests of the weak equivalence principle with ordinary matter would also be an important constraint as far as the relation between gravity and antimatter is concerned. Several models of elementary particles have been proposed in which there are new long range forces between neutral particles (e.g. Scherk 1979; Moody and Wilczek 1984; Fayet 1990; Peccei, Sola' and Wetterich 1987; Taylor and Veneziano 1988). Generally they lead to forces between two bodies proportional to the product of two quantum numbers ---e.g. their barion numbers--- and as such they violate the Equivalence Principle . However, their state of development is very uncertain and at present experiments on the Equivalence Principle do not have a precise theory to test and a corresponding target accuracy. More recent work (Damour and Polyakov 1994) has shown that an EP violation has to be expected, but only below the 10-12 level reached so far; whether this amazing coincidence is real, only experiments will tell. Although only a space experiment can give several orders of magnitude improvement in EP testing accuracy, a ground experiment capable to reach a sensitivity of a few parts in 1013 with laboratory bodies would be of great value. Presently the best test of the Equivalence Principle, more accurate than torsion balance laboratory tests, is performed with the Earth and the Moon falling toward the Sun, the Earth--Moon distance being measured by lunar laser ranging (LLR) to the corner cube laser reflectors left by the astronauts on the surface of the Moon. Were the Earth and the Moon to be attracted differently by the Sun, a physical model based on conventional newtonian gravity with general relativistic corrections would not be able to make predictions reconciliable with the observed LLR data (accurate to better than a cm ). This experiment is now about one order of magnitude more accurate than torsion balance laboratory experiments (Dickey et al. 1994; Williams, Newhall & Dickey 1996). So we have an anbiguity of interpretation of LLR since it both tests the Equivalence Principle (through its consequence, the Universality of Free Fall) for different materials (Earth's iron vs Moon's silicates) and for gravitational self--energy effects in the Earth (testing gravity's pull on gravitational energy). A more accurate EP test with laboratory sized bodies (for which the gravitational self--energy is negligible) would be of great value, so LLR could be uniquely interpreted as testing the relativistic structure of metric gravity theories. In particular, bodies should be chosen with composition similar to the composition of the Earth and the Moon.
1.2 The Advantages Of Space
There is a tendency in ground experiments of physics, as well as in facilities for astronomical observations, to become big enterprises involving many scientists/engineers and large fundings, often lasting several years. By contrast, scientific space missions tend to become smaller, faster and cheaper; so the gap between the two is decreasing. Yet, doing science in space is still a challenge in itself. Therefore, no space experiment should be proposed unless there is a very good reason for it to be done in space. As far as testing the Equivalence Principle is concerned, the crucial advantage of a space experiment in low Earth orbit is that the driving signal in the field of the Earth (long range) is given by the entire value of its gravitational acceleration. For a spacecraft at 520, km altitude this amounts to GMÅ /a2 ~ 840 cm/s2 ( G is the universal constant of gravity, MÅ the mass of the Earth and a the orbital radius of the satellite) as opposed to a maximum value of ~ 1.69 cm/s2 on the ground in the field of the Earth (at 45° latitude) and ~ 0.6 cm/s2 0.6 in the field of the Sun. By contrast, a short range EP experiment has nothing to gain from going into space since much bigger source masses are available on the ground. Such an experiment has however been proposed, under the name of SREP (Paik et al. 1993) and also submitted to ESA for the M3 Medium Science Mission competition; but evidently could not be pursued any further. In the early days of the space age ordinary people and scientists alike dreamed of going into space. Physicists in particular were fascinated by the emptiness and quietness of space, which appeared to be the ideal environment for many experiments, especially gravity experiments, limited by too many perturbations on Earth. As dreams faded away and reality began, it became apparent that space is not empty and spacecraft are not quiet ; at least, not as much to automatically compensate for the disadantage of the experiment becoming inaccessible to one's hands. Nowadays the space environment is far better understood, and a few statements can be made which are not likely to be disproved. The absence of seismic noise can no longer be quoted as a reason for moving to space, since on--board of any space structure there is vibrational noise instead, while down on Earth experimentalists have learned how to cope with seismic noise very effectively. Also, space in far from being empty : residual atmosphere (in low Earth orbits), photons from solar radiation, charged particles ... make physics experiments in space ---particularly gravitational ones--- far from straightforward. However, the main advantage of space is still there: the gravitational attraction of the Earth is largely compensated by the centrifugal force due to the orbital motion of the spacecraft and there is no such thing like the 1 g ~103 cm/s2 local acceleration of gravity that shapes our everyday life on Earth by giving a weight to every object. In addition and more importantly, the largest acceleration on--board is many orders of magnitude smaller than 1 g , how much precisely depending on the orbit, the spacecraft, the body on--board that we are considering (e.g. whether it is suspended or free floating, or else rigidely connected to the spacecraft, whether it is close to the center of mass of the spacecraft or far away from it). In GG the largest acceleration on all bodies inside is about a factor 108 smaller than 1 g . Evidentely a ratio by one hundred million times between the force that has to be overcome in order to suspend the same body in the ground laboratory or inside the GG spacecraft makes a big difference in the problems to be faced; it is indeed possible to suspend 100 kg with the same suspensions that would be used on Earth for 1 milligram . Weightlessness , not the absence of seismic noise, is therefore the true advantage of space that must be exploited. GG has been specifically designed for weightlessness to provide numerous advantages: self--centring, weak mechanical coupling, no electric charging, vibration isolation, all of them crucial for the small force EP differential experiment, all deriving only from using mechanical suspensions appropriate for the space environment. An EP space experiment in low Earth orbit offers the crucial advantage of a signal about a factor of a thousand bigger than on Earth; the challenge of a fully automated remote controlled experiment can be traded off against the advantages of weightlessness. An accuracy of 1 part in 1017 in h (which means an EP violation signal as small as ~ 8.4 10-15 cm/s2 would be a five order of magnitude improvement with respect to the best ground tests. Even with further progress in ground experiments (e.g. to an accuracy of 1 part in 1013 , possibly 1014 ) a space mission would undoubdtely mean a great leap forward allowing space scientists to probe a totally unknown, highly interesting field of physics like no other ground experiment can even dream of.
1.3 The Technological Objective
The technological goal of the Galileo Galilei (GG) mission is a full, comprehensive test of FEEP (Field Emission Electric Propulsion) thrusters for fine drag compensation. FEEP thrusters have been invented, designed and developed by ESA in Europe and will most probably become an essential component of all space missions which require measurement of small forces. In such missions ordinary impulsive thrusters cannot be used because they produce noise on the spacecraft at all frequencies which would disturb the experiment inside. Small force missions like GG and LISA (Laser Interferometry Space Antenna) (Bender et al. 1995) do greatly benefit from the numerous adavantages of FEEP thrusters: high specific impulse, negligible amount of propellant and no moving parts; fine electric tuning and consequent high level of proportionality. By contrast, He thruster developed in the US for missions such as GP--B (Gravity Probe B, the Stanford cryogenic gyroscope mission funded by NASA to measure various effects of General Relativity, now close to flying) and STEP (Satellite Test of the Equivalence Principle, the cryogenic mission proposal originated at Stanford to test the Equivalence Principle) have low specific impulse, need a large amount of propellant and proportionality is ensured by mechanical valves. He thrusters appear to be the only viable solution for these missions since they carry anyway large amounts of He on--board (to make the experiment cryogenic) and need to eliminate the boiled off He from the cryostat without producing unwanted translational or rotational perturbations on the spacecraft to the required drag--free level. The use of FEEP thrusters in STEP (instead of He thrusters) has been envisaged in the ESA--only M3 assessment study report (Blaser et al. 1994), so as to use a european technology for drag--free control. Even if FEEP thrusters were allowed by the power budget, He from the cryostat would still need to be eliminated in a controlled, smooth manner, which is what He thrusters are meant for. In fact, the idea of FEEP on STEP did not survive a closer scrutiny and was abondoned during industrial Phase--A study (Blaser et al. 1996). In Europe ESA has funded FEEP activity for almost 25 years by now. LISA, the third cornerstone project of the Horizon 2000 Plus science programme (scheduled for the year 2016 ) is non-cryogenic and relies on FEEP thrusters to meet stringent requirements on drag--free control. In the NASA led MiniSTEP project ESA is offered to particpate by providing the mission operations, the proof masses and the drag--free control system (Swanson and Lee 1996). Since He thrusters are american technology (and will presumably remain so) ESA would contribute the software and electronics, with no control over the complete drag compensation system for future use in Europe were the need for it to arise. By contrast, ESA and Europe have acquired a clear leadership on FEEP technology, there is a future for it ---in Europe and probably worldwide--- resources have been already invested for many years; a final effort to fly FEEP thrusters and demonstrate their capabilities appears to be the most natural choice in the interest of ESA. A test flight of firing capability for a given timespan is certainly first priority; however the real use of FEEP thrusters for fine drag--free control in small force space experiments should be demonstrated as soon as possible. Only after such (successful) demonstration FEEP technology will become really appealing for space scientists and space agencies alike. Awaiting for a cornerstone mission like LISA in 2016 at earliest, for a full demonstration flight means another 20 years (at least) with no conclusive result on FEEP technology. Instead, this technology can be fully demonstrated much sooner on the small, low--cost, GG scientific mission. A key element of the GALILEO GALILEI (GG) mission is the use of FEEP thrusters to reduce the effect of non gravitational forces acting on the spacecraft by a factor 10-2 in the plane of the signal ( ~ the orbit plane) and by a factor 102 along the spin axis ( ~ perpendicular to the orbit plane), in the frequency range from 10-4 , Hz to 10-2 , Hz . It is generally believed that a spacecraft for testing the Equivalence Principle should be capable to compensate for the effect of non gravitational forces (mostly drag from the residual atmosphere) acting on its surface. An EP experiment needs 3 bodies: a source mass and 2 test bodies. Violation produces a tiny differential acceleration of one test body with respect to the other, unreconciliable with conventional physics. Non gravitational forces affect the test bodies suspended inside the spacecraft as inertial forces applied to their centers of mass (gyroscopic effects can be made small). Inertial forces are many orders of magnitude larger than the expected signal, but they are -- in principle -- common mode , i.e. they affect the test bodies identically leaving no differential acceleration to compete with the expected EP violation signal. In reality, since the test bodies cannot be identically suspended (nor perfectly balanced if they are coupled) the common mode effect of inertial forces can only be rejected to some extent, and a residual differential effect remains which competes with the signal. A given sensitivity to differential forces results from the combination of a rejection of common mode effects by the coupled system of test masses and a compensation of non gravitational forces by the spacecraft. If it is possible to guarantee a high level of common mode rejection ---depending on the test bodies experimental design--- the spacecraft can have no drag compensation at all. Indeed, GG was originally conceived as an experiment in a non drag--free spacecraft (Bramanti, Nobili and Catastini 1992; Nobili et al. 1993; Nobili et al. 1994). If the price to pay for drag compensation are perturbations from moving mass on--board (the propellant), it may be a reasonable choice to give up drag compensation while concentrating instead on a high level of common mode rejection by the test masses and minimizing the effects of non gravitational forces with a very compact spacecracft (low area--to--mass ratio) at appropriate altitude. This is why the GG spacecraft, in its non drag--free version, was more massive than the GG drag--free spacecraft presented here. However, it was pointed out by A. Milani (1993) that if drag can be compensated by FEEP thrusters, which need only a negligible amount of propellant, it is indeed a good choice to make the spacecraft drag--free, thus reducing its total mass and relaxing the requirement on common mode rejection by the test bodies. In so doing some of the complexity of the payload (common mode rejection) is inevitably transferred to the spacecraft (drag--free control system), but the total mass is reduced and the experiment can be made, overall, more sensitive to differential effects. In spite of the small signal they aim to, space missions for testing the Equivalence Principle do not have very stringent requirements on drag compensation. This is precisely because the signal of interest is differential while perturbing common mode forces like the inertial ones can be rejected, to some extent, by the test bodies themselves. By comparison, the requirement on drag--free level for each one of the (six) LISA spacecraft (for the expected gravity wave signals not to be disturbed by non gravitational forces) is far more stringent than in GG: the largest non gravitational force on the spacecraft is about the same ( ~1 dyn ), and in the current baseline FEEP thrusters are required to reduce it by a factor of about 3× 107 (as opposed to 104 at most in GG) in a similar frequency band.
1.4 GG vs Other Projects
Since the mid 70s till the early 90s testing the Equivalence Principle in space was dominated by the STEP project (Worden and Everitt 1973; Worden 1976; Worden 1978; Barlier et al. 1991; Blaser et al. 1993; Blaser et al. 1994; Blaser et al. 1996). STEP has originated at Stanford University, USA in close relation with GP--B, the main Stanford project in fundamental physics. Although the requirements are not the same, being in some cases more stringent for STEP than for GP--B, the two missions share key hardware components: a superfluid He dewar, He thrusters for drag compensation and SQUID (Superconducting Quantum Interference Device) sensors. The fact that two space projects of significant complexity and cost were proposed by the same University, in fact by the same research group, was seen by many as weakening the chances for approval of STEP, due to the tight competition for space missions from research groups all over the country. To the contrary, the STEP (now MiniSTEP) proposers push NASA to support it for flight on the grounds that this is a way for NASA of capitalizing on the large fundings it has put, and is putting, in GP--B, now close to flying. In so doing they stress all commonalities of the MiniSTEP technology with the technology of GP--B, making the point that MiniSTEP can fly just immediately after GP--B at small extra efforts and cost. The close relationship with GP--B inevitably has had the effect of constraining STEP within the technology of GP--B, no matter whether this is ideal for EP testing or not. In point of fact, key technological features of the STEP mission have been modified within GEOSTEP, a proposal from the french space agency CNES (CNES, ``GEOSTEP Project'' 1996). GEOSTEP maintains the original conceptual design of STEP for EP testing while making substantial changes in the hardware. The changes concern two key components: the dewar and the sensors. The main change is in the dewar, driven by the need to reduce perturbations on the test bodies by He in the cryostat. French scientists are led to accept a slightly higher temperature as a trade off for a dewar design that can reduce such dangerous perturbations. The sensors are well tested capacitance sensors, which can meet the requirement on the relative displacements of the test masses to be detected. Since refrigeration is still provided by He , drag compensation is also based on He thrusters. The bus is derived from the french small satellite platform PROTEUS. After presentation of GEOSTEP and MiniSTEP to the Fundamental Physics Advisory Group of ESA (FPAG) for a comparative assessment in April 1996 MiniSTEP was unanimously rated superior to GEOSTEP. The presentation of GEOSTEP was based on a Report submitted by CNES; for MiniSTEP a Preprint Report (Everitt et al. 1996) was submitted of a study conducted by NASA with contribution from ESA. ESA contribution to MiniSTEP was provided during the ESA--only Phase A study of STEP for the M3 competition. "GALILEO GALILEI'' (GG) was devised at the University of Pisa, Italy in the early 90s starting from the assumption that time had come for a space experiment on the Equivalence Principle to be rethought completely anew (Bramanti, Nobili and Catastini 1992; Nobili et al. 1993; Nobili et al. 1994; Nobili et al. 1995). From STEP GG takes the idea of concentric cylindrical test masses, but then follows its own driving concepts: a high frequency signal; low stiffness mechanical suspensions and mechanical coupling of the test bodies; a non cryogenic experiment; a small mission devoted to EP testing only. A high frequency signal ( 5 Hz ) comes from the need to make its detection easier because less affected by the ubiquitous 1/f noise . It is obtained with a spacecraft stabilized (passively) by one axis rotation. Together with mechanical suspensions of very low stiffness (possible thanks to weightlessness) the fast spin provides numerous advantages: an effective vibration isolation, supercritical rotation of the test bodies which behave almost like free rotors, many `` dangerous '' perturbations will become DC (nearby mass anomalies, parasitic capacitances, patch effects, non uniform thermal expansion ....). Mechanical suspensions also allow the test masses to be electrically grounded, thus eliminating the major effect of electrostatic charging, which is known to haunt all gravitational experiments, STEP among them. GG is a room temperature experiment, the advantages of cryogenics having been traded off against the disadvantages of nearby moving He mass and the need for mechanically tuned He thrusters. Instead, air drag on GG is partially compensated with FEEP thrusters (ESA technology), which have high specific impulse, need a negligible amount of Cs and are electrically tuned. However, it is worth mentioning that fast spin would make a future cryogenic version of GG quite appealing as far as perturbations from the refrigerating material are concerned. The large centrifugal force would dominate over tidal deformations pushing the refrigerating material outwards all the time and thus minimizing its own perturbations on the experiment; evaporation could be allowed from along the spin axis only (``top'' and ``bottom'') thus minimizing perturbations on the spacecraft. Another EP testing experiment has been proposed (Lorenzini et al. 1994; 1996) where the signal is modulated at 1 Hz by spinning the detector (cryogenic at liquid He temperature). The capsule is in sub--orbital flight with free falling time of 30 s . The expected accuracy is of 5 parts in 1015. Last but not the least, GG was meant from the start to perform EP testing only, like the present MiniSTEP and GEOSTEP projects. This allowed us to optimize the experimental design of the spacecraft, its orbit and attitude as well as the payload, for EP testing. The choice, which became dominant within the study teams of STEP in the M2 and M3 competitions, was to broaden the number of tasks to be performed. The proposed gravity mission based on the so--called SEE ( Satellite Energy Exchange method (Sanders and Deeds 1992) also offers several objectives. Instead, we have tried to respond to the new demand, which is coming from many national space agencies alike for smaller, faster, and cheaper missions. Although it is apparent that not all space missions can be small, fast and cheap , there is no doubt that project durations of decades, which inevitably tend to absorb most of the financial resourses available for one particular area of space science, are becoming less and less appealing to space agencies. In this respect ESA is known to be atypical, due to its multinational structure, and the LISA cornerstone project of Horizon 2000 Plus can be an important exception, provided it will survive the financial cuts of ESA Science Directorate and fly within 20-25 years from its first approval. In particular, the need for a small, fast and cheap mission in the area of fundamental physics appears to be a necessary first step in Europe where the corresponding scientific community still needs to establish itself as part of the community of space science by flying its first mission. Scientific research on GG has been supported by ASI (Agenzia Spaziale Italiana) since 1993. In the years 1994 and 1995 a national collaboration on the GG project involving eight scientific institutions in Italy has been funded by ASI for feasibility study and for the realization of a payload prototype on the ground. In October 1995 the italian space industry Laben has initiated a collaboration on GG at its own expenses. Proel, a division of Laben in Florence has made its well equipped laboratories available for the payload prototype experiment GALILEO GALILEI On The Ground (GGG). After ESA decision in April 1996 not to select STEP for M3, ASI has decided to fund both Alenia Spazio and Laben for a Pre-Phase A study of GG. Alenia Spazio was prime contractor of the industrial Phase A study of STEP in the competitions for both the M2 and M3 medium size missions of ESA. Another mission concept has been proposed which shares some of the features of GG. This is the project Eotvos (Blaser et al. 1996), in which the orbit is equatorial, the system is spin--stabilized, the spin axis is perpendicular to the orbit plane, there is electrostatic sensing and no cryostat. The main differences with respect to GG are the slow spin rate ( 1000 s vs 0.2 s of spin period) and the fact that the spacecraft and the payload are completely decoupled. A slow spin rate was never considered for GG (the first spinning test of the Equivalence Principle in space was proposed by Chapman and Hanson 1970) because of the higher 1/f noise, and because it would not provide, in the presence of mechanical suspensions, a supercritical state of rotation with its numerous advantages. Instead, the possibility for the outer spacecraft and the payload to be totally decoupled has been taken into consideration. The idea of such loose drag--free system (named then optical drag-free ) was in fact at the basis of the NEWTON proposal for the measurement of the universal constant of gravity G in space (Nobili et al. 1989; Nobili et al. 1990; Nobili et al. 1993). A mechanical coupling between the spacecraft and the Pico Gravity Box (PGB) laboratory with low stiffness (electrically conductive) mechanical suspensions is preferable for two main reasons. In the first place, to avoid electrostatic interaction between the spacecraft and the payloads. Charging of the test bodies is known to be a serious matter of concern in all gravitational experiments; charging of the payload and the spacecraft inner surface can similarly occur unless they are electricaly connected (best with gold coating) so that all charges move to the outmost conductive surface and only small patch effects remain. Since electrostatic interaction between decoupled spacecraft and payload to the level of drag--free requirement cannot be excluded, there is no way for it to be compensated by the thrusters since it acts directly on the payload (which is also the driving test mass for the drag--free control). This means that the payload is not in fact in the presumed free falling, pure gravitational motion. Secondly, if the spacecraft and the PGB are coupled mechanically by low stiffness springs these serve the purpose of damping any relative conical motions (including Eulerian precessions) which would inevitably arise if the spacecraft is put into rotation around an axis which does not coincide exactly with the axis of maximum moment of inertia (similarly to the Chandler Wobble of the rotation axis of the Earth inside the planet). This makes passive spin axis stabilization possible without even resorting to the use of liquid damping, which would be inappropriate for an EP experiment.
References
E.G. Adelberger, C.W. Stubbs, B.R. Heckel, Y. Su, H.E. Swanson, G. Smith, J.H. Gundlach and W.F. Rogers, Phys. Rev. D 42 (1990 ) 3267.
F. Barlier, J.P. Blaser, G. Cavallo, T. Damour, R. Decher, C.W.F. Everitt, F. Fuligni, M. Lee, A.M. Nobili, K. Nordtvedt, O. Pace, R. Reinhard, and P.W. Worden Jr., STEP, Assessment Study Report ESA/NASA SCI(91)4, (1991).
P. Bender, I. Ciufolini, K. Danzmann, W. Folkner, J. Hough, D. Robertson, A. R "udiger, M. Sandford, R. Shilling, B. Schutz, R. Stebbins, T. Sumner, P. Touboul, S. Vitale, H. Ward and W. Winkler, LISA, Pre-Phase A Report (1995).
N. Beverini, J.H. Billen, B.E. Bonner, L. Bracci, R.E. Brown, L.J. Campbell, D.A. Church, K.R. Crandall, D.J. Ernst, A.L. Ford, T. Goldman, D.B. Holtkamp, M.H. Holzscheiter, S.D. Howe, R.J. Hughes, M.V. Hynes, N. Jarmie, R.A. Kenefick, N.S.P. King, V. Lagomarsino, G. Manuzio, M.M. Nieto, A. Picklesimer, J. Reading, W. Saylor, E.R. Siciliano, J.E. Stovall, P.C. Tandy, R.M. Thaler, G. Torelli, T.P. Wangler, M. Weiss and F.C. Witteborn, (CERN/PSCC/86-2 PSSC/P-64, 1986), (Los Alamos National Laboratory Report LA-UR-86-260, 1986).
J.P. Blaser, M. Bye, G. Cavallo, T. Damour, C.W.F. Everitt, A. Hedin, R.W. Hellings, Y. Yafry, R. Laurance, M. Lee, A.M. Nobili, H.J. Paik, R. Reinhard, R. Rummel, M.C.W. Sandford, C. Speake, L. Spencer, P. Swanson and P.W. Worden Jr., STEP, Report on the Phase A Study ESA/NASA SCI(93)4, (1993).
J.P. Blaser, A.M. Cruise, T. Damour, J. Leon, H.J. Paik and R. Rummel, STEP, Assessment Study Report ESA SCI(94)5 (1994).
J.P. Blaser, J. Cornelisse, A.M. Cruise, T. Damour, F. Hechler, M. Hechler, Y. Jafry, B. Kent, N. Lockerbie, H.J. Paik, A. Ravex, R. Reinhard, R. Rummel, C. Speake, T. Sumner, P. Touboul and S. Vitale STEP, Report on the Phase A Study ESA SCI(96)5 (1996).
J.P. Blaser, N. Lockerbie, H.J. Paik, C. Speake and S. Vitale, COSPAR Abstracts (1996) 419. V.B. Braginsky and V.I. Panov, Sov. Phys. JEPT 34 (1972) 463. D. Bramanti, A.M. Nobili and G. Catastini, Phys. Lett. A 164 (1992) 243.
P.K. Chapman and A.J. Hanson, Proceedings of the Conference on Experimental Tests of Gravitational Theories Cal. Tech. JPL TM no. 33-499 (1970) 228. CNES, GEOSTEP Project (1996). T. Damour and A.M. Polyakov, Nucl. Phys. B 423 (1994) 532.
J.O. Dickey, P.L. Bender, J.E. Faller, X X Newhall. R.L. Ricklefs, J.G. Ries, P.J. Shelus, C. Veillet, A.L. Whipple, J.R. Wiant, J.G. Williams and C.F. Yoder, Science 265 (1994) 482.
C.W.F. Everitt, N.A. Lockerbie, P.N. Swanson and P.W. Worden Jr., MiniSTEP Preprint Report (1996). P. Fayet, Nucl. Phys. B 347 (1990) 743.
E.C. Lorenzini, I.I. Shapiro, F. Fuligni, V. Iafolla, M.L. Cosmo, M.D. Grossi, P.N. Cheimets and J.B. Zielinski, Harvard-Smithsonian Center for Astrophysics Preprint Series No. 3966 (1994) also in Il Nuovo Cimento B .
E.C. Lorenzini, V. Iafolla, P. Orlando and M.D. Grossi, COSPAR Abstracts (1996) 415.
A. Milani, private communication (1993)
J.E. Moody and F. Wilczek, Phys. Rev. D 30 (1984) 130.
A. M. Nobili, A. Milani, E. Polacco, I. W. Roxburgh, F. Barlier, K. Aksnes, C.W. F. Everitt, P. Farinella, L. Anselmo and Y. Boudon, NEWTON, proposal for the M2 medium size mission of ESA (1989).
A. M. Nobili, A. Milani, E. Polacco, I. W. Roxburgh, F. Barlier, K. Aksnes, C.W. F. Everitt, P. Farinella, L. Anselmo and Y. Boudon, ESA Journal 14 (1990) 389.
A. M. Nobili, A. Milani, E. Polacco, D. Bramanti, G. Catastini, I. W. Roxburgh, F. Barlier, K. Aksnes, C.W. F. Everitt, P. Farinella, L. Anselmo, Y. Boudon, NEWTON, proposal for the M3 medium size mission of ESA (1993).
A. M. Nobili, D. Bramanti, E. Polacco, G. Catastini, E. Rossi, B. Bertotti, P. G. Bizzeti, V. B. Braginsky, V. P. Mitrofanov, W. Flury, A. Brillet, T. Quinn, F. Barlier, C. Marchal, A. Bernard, P. Touboul, A.H. Cook, J. Hough, I.W. Roxburgh and A. Polnarev, Galileo Galilei (GG), proposal for the M3 medium size mission of ESA (1993).
A. M. Nobili, D. Bramanti, E. Polacco, G. Catastini, G. Genta, E. Brusa, V. B. Mitrofanov, A. Bernard, P. Touboul, A. J. Cook, J. Hough, I. W. Roxburgh, A. Polnarev, W. Flury, F. Barlier, C. Marchal, Proposed New Test of the Equivalence Principle in Space, PISA Preprint on Astrophysics and Space Mechanics (1994); Revised, February 1995, available on line: http://adams.dm.unipi.it/publications/gg.ps.gz
A.M. Nobili, D. Bramanti, G. Catastini, E. Polacco, A. Milani, L. Anselmo, M. Andrenucci, S. Marcuccio, A. Genovese, F. Scortecci, G. Genta, E. Brusa, C. Del Prete, D. Bassani, G. Vannaroni, M. Dobrowolny, E. Melchioni, C. Arduini, U. Ponzi, F. Curti, G. Laneve, D. Mortari, M. Parisse, F. Cabiati, E. Rossi, A. Sosso, G. Zago, S. Monaco, G. Gori Giorgi, S. Battilotti, L. D'Antonio and G. Amicucci, The Journal of the Astronautical Sciences 43 3 (1995) 219.
H.J. Paik, J.P. Blaser, F. Hechler and Y. Jafry, STEP Symposium , Pisa (1993). R.D. Peccei, J. Sola C. Wetterich, Phys. Lett. B 195 (1987) 183.
P.G. Roll, R. Krotkov and R.H. Dicke, Ann. Phys. (N.Y.) 26 (1964) 442.
A.J. Sanders and W.E. Deeds, Phys. Rev. D 46 (1992) 489.
J. Scherk, Phys. Lett. 88B (1979) 265.
Y. Su, B.R. Heckel, E.G.Adelberger., J.H. Gundlach, M. Harris, G.L. Smith and H.E. Swanson, Phys. Rev. D 50 (1994) 3614.
P.N. Swanson and M.C. Lee, COSPAR Abstracts (1996) 417. T.R. Taylor and G. Veneziano, Phys. Lett. B 213 (1988) 450.
C.M. Will, Int. J. Mod. Phys. D 1 (1992) 13.
J. G. Williams, X X Newhall and J. O. Dickey, Phys. Rev. D 53 (1996) 6730.
P.W. Worden Jr., and C.W.F. Everitt, 1973, Proceedings Int. School of Physics E. Fermi, Course LVI: Experimental gravitation Academic Press, N.Y. (1973) 381.
P.W. Worden, Jr., PhD thesis Stanford University (1976). P.W. Worden, Jr., Acta Astronautica 5 (1978) 27.
A. Milani, A.M. Nobili and P. Farinella, Non--Gravitational Perturbation and Satellite Geodesy (Adam Hilger, Bristol, 1987).
Back to Cover
(Anna Nobili- nobili@dm.unipi.it)
Last edited May 12, 1998