In his "Discorsi e dimostrazioni matematiche ..." published in Leiden in 1638 while he was blind and under house arrest in Italy (Galilei, 1638) Galileo reported results of experiments carried out almost forty years earlier with pendula and the inclined plane. He formulated with astonishing neatness what lately became known as the Principle of Equivalence, according to which all bodies fall in the same way regardless of their mass and composition: ...veduto, dico questo, cascai in opinione che se si levasse totalmente la resistenza del mezzo, tutte le materie descenderebbero con eguali velocitŕ (...having observed this I came to the conclusion that, if one could totally remove the resistance of the medium, all substances would fall at equal speeds). About 80 years after Galileo's first experiments Newton went further, actually recognizing the equivalence of mass and weight. Newton regarded this equivalence as so important that he devoted to it the opening paragraph of the Principia, where (Definition I) he stated: "this quantity that I mean hereafter under the name of ...mass ...is known by the weight ...for it is proportional to the weight as I have found by experiments on pendulums, very accurately made..." (Cajori, 1934).
At the beginning of the ![]() century, almost 300 years since Galileo's work, Einstein realized that
because of the equivalence between the gravitational (passive) mass
century, almost 300 years since Galileo's work, Einstein realized that
because of the equivalence between the gravitational (passive) mass ![]() and the inertial mass
and the inertial mass ![]() (i.e. the weak equivalence
principle), the effect of gravitation is locally equivalent to the effect of an
accelerated frame and can be locally cancelled. In a freely falling system all masses fall
equally fast, hence gravitational acceleration has no local dynamical effects. Einstein
then generalized the weak equivalence principle to the strong equivalence
principle, on which he based his theory of General Relativity. The strong
equivalence principle states that in an electromagnetically shielded laboratory,
freely falling and nonrotating, the laws of Physics - including their numerical content -
are independent of the location of the laboratory. In such a laboratory all particles free
of nongravitational forces move with the same acceleration. That is to say, the effects
of gravity, according to General Relativity, are equivalent to the effects of living in a
curved spacetime. In this sense the weak equivalence principle expresses the very
essence of General Relativity and as such it deserves to be tested as accurately as
possible. In the last 30 years since the advent of the space age General Relativity has
been subject to extensive experimental testing as never before in its first 50 years of
existence, and so far it has come out having no real competitors (e.g. Will, 1992); the crucial area where experimental
gravitation is likely to play an important rôle is in the verification of the weak
equivalence principle itself, since it is tantamount to testing whether gravitation can be
ascribed to a metric structure of spacetime.
(i.e. the weak equivalence
principle), the effect of gravitation is locally equivalent to the effect of an
accelerated frame and can be locally cancelled. In a freely falling system all masses fall
equally fast, hence gravitational acceleration has no local dynamical effects. Einstein
then generalized the weak equivalence principle to the strong equivalence
principle, on which he based his theory of General Relativity. The strong
equivalence principle states that in an electromagnetically shielded laboratory,
freely falling and nonrotating, the laws of Physics - including their numerical content -
are independent of the location of the laboratory. In such a laboratory all particles free
of nongravitational forces move with the same acceleration. That is to say, the effects
of gravity, according to General Relativity, are equivalent to the effects of living in a
curved spacetime. In this sense the weak equivalence principle expresses the very
essence of General Relativity and as such it deserves to be tested as accurately as
possible. In the last 30 years since the advent of the space age General Relativity has
been subject to extensive experimental testing as never before in its first 50 years of
existence, and so far it has come out having no real competitors (e.g. Will, 1992); the crucial area where experimental
gravitation is likely to play an important rôle is in the verification of the weak
equivalence principle itself, since it is tantamount to testing whether gravitation can be
ascribed to a metric structure of spacetime.
The total mass-energy of a body is the sum of many terms corresponding
to the energy of all the conceivable interactions and components: ![]() . For two bodies A and B
of different composition the Eötvös parameter
. For two bodies A and B
of different composition the Eötvös parameter ![]() can be generalized into
can be generalized into
![]()
such that a non-zero value of ![]() would define the violation of equivalence between the inertial and
gravitational mass-energy of the k-th kind. For instance, the rest mass would
contribute (as a fraction of the total) for
would define the violation of equivalence between the inertial and
gravitational mass-energy of the k-th kind. For instance, the rest mass would
contribute (as a fraction of the total) for ![]() ; the nuclear binding energy for
; the nuclear binding energy for ![]() , the mass difference between neutron and proton for
, the mass difference between neutron and proton for ![]() (A being the number
of protons plus neutrons and Z the number of protons in the nucleus), the
electrostatic energy of repulsion in the nuclei for
(A being the number
of protons plus neutrons and Z the number of protons in the nucleus), the
electrostatic energy of repulsion in the nuclei for ![]() , the mass of electrons for
, the mass of electrons for ![]() , the antiparticles for
, the antiparticles for ![]() , the weak interactions responsible of
, the weak interactions responsible of ![]() decay for
decay for ![]() . From the point of view of conventional field theory, the
verification of all these separate equivalence principles corresponds to a very peculiar
coupling of each field to gravity; whether and why it should be so in all cases is a
mystery. Let us consider the case of antiparticles. A peculiarity of gravity, strictly
related to the Equivalence Principle (EP), is that there is so far no evidence for antigravity,
namely for the possibility that matter is gravitationally repelled by antimatter. A
negative ratio of inertial to gravitational mass would obviously violate the equivalence
principle and forbid any metric theory of gravity. Yet, there are theoretical formulations
which would naturally lead to antigravity (Scherk,
1979), and experiments have been proposed to directly explore the relation between
gravity and antimatter. The idea is to make a Galileo-type mass dropping experiment using
a proton and an antiproton in order to check whether they both fall like ordinary matter
or not. The experiment was proposed to CERN by an international team of scientists (Beverini et al., 1986). Unfortunately, while
experiments concerning the inertial mass of antiparticles have been highly successful, and
these are very accurately known, gravitational experiments (i.e. involving the
gravitational mass of antiparticles) are extremely difficult because of the far larger
electric effects, such as those due to stray electric fields in the drift tube. Indeed,
the latter have so far hindered the experiment mentioned above. In absence of such direct
tests, an improvement by several orders of magnitude of current tests of the weak
equivalence principle with ordinary matter would also be an important constraint as far as
the relation between gravity and antimatter is concerned. Several models of elementary
particles have been proposed in which there are new long range forces between neutral
particles. Generally they lead to forces between two bodies proportional to the product of
two quantum numbers - e.g. their barion numbers - and as such they violate the equivalence
principle. However, their state of development is uncertain and at present experiments on
the weak equivalence principle do not have a precise theory to test and a corresponding
target accuracy.
. From the point of view of conventional field theory, the
verification of all these separate equivalence principles corresponds to a very peculiar
coupling of each field to gravity; whether and why it should be so in all cases is a
mystery. Let us consider the case of antiparticles. A peculiarity of gravity, strictly
related to the Equivalence Principle (EP), is that there is so far no evidence for antigravity,
namely for the possibility that matter is gravitationally repelled by antimatter. A
negative ratio of inertial to gravitational mass would obviously violate the equivalence
principle and forbid any metric theory of gravity. Yet, there are theoretical formulations
which would naturally lead to antigravity (Scherk,
1979), and experiments have been proposed to directly explore the relation between
gravity and antimatter. The idea is to make a Galileo-type mass dropping experiment using
a proton and an antiproton in order to check whether they both fall like ordinary matter
or not. The experiment was proposed to CERN by an international team of scientists (Beverini et al., 1986). Unfortunately, while
experiments concerning the inertial mass of antiparticles have been highly successful, and
these are very accurately known, gravitational experiments (i.e. involving the
gravitational mass of antiparticles) are extremely difficult because of the far larger
electric effects, such as those due to stray electric fields in the drift tube. Indeed,
the latter have so far hindered the experiment mentioned above. In absence of such direct
tests, an improvement by several orders of magnitude of current tests of the weak
equivalence principle with ordinary matter would also be an important constraint as far as
the relation between gravity and antimatter is concerned. Several models of elementary
particles have been proposed in which there are new long range forces between neutral
particles. Generally they lead to forces between two bodies proportional to the product of
two quantum numbers - e.g. their barion numbers - and as such they violate the equivalence
principle. However, their state of development is uncertain and at present experiments on
the weak equivalence principle do not have a precise theory to test and a corresponding
target accuracy.
The best ground experiments to test the weak equivalence principle have
employed one of the most sensitive devices in the history of Physics: the torsion balance
(Eötvös et al., 1922; Roll et al., 1964; Braginsky & Panov, 1972). More recently,
thanks to the debate on the so-called fifth-force raised by Fishbach et al. (1986), a series of revised
torsion balance experiments has been carried out reaching an accuracy of about 1 part
in ![]() (Adelberger et al., 1990; Su et al., 1994). The main novelty is that the
torsion balance is rotating in order to modulate the signal at higher frequency.
(Adelberger et al., 1990; Su et al., 1994). The main novelty is that the
torsion balance is rotating in order to modulate the signal at higher frequency.
The crucial advantage of an EP space experiment in low Earth orbit is
that the driving signal in the field of the Earth is given by the entire value of
its gravitational acceleration. At ![]() altitude this amounts to
altitude this amounts to ![]() (G is the universal constant of gravity,
(G is the universal constant of gravity, ![]() the mass of the Earth and R
the orbital radius of the satellite) as opposed to a maximum value of
the mass of the Earth and R
the orbital radius of the satellite) as opposed to a maximum value of ![]() for a torsion balance on the ground in the
field of the Earth (at
for a torsion balance on the ground in the
field of the Earth (at ![]() latitude)
and
latitude)
and ![]() in the field of the Sun. In
contrast a short range EP experiment has nothing to gain from going into space, since much
bigger source masses are available on the ground. The scientific objective of the
nondrag-free GG mission proposed here is to test the weak equivalence principle in low
Earth orbit to 1 part in
in the field of the Sun. In
contrast a short range EP experiment has nothing to gain from going into space, since much
bigger source masses are available on the ground. The scientific objective of the
nondrag-free GG mission proposed here is to test the weak equivalence principle in low
Earth orbit to 1 part in ![]() . This
requires to measure the effects of a very small differential acceleration
. This
requires to measure the effects of a very small differential acceleration ![]() . An accuracy of
. An accuracy of ![]() in
in ![]() would be a four order of magnitude improvement with
respect to the current best ground tests. Even with a further improvement of ground
results (e.g. to an accuracy of 1 part in
would be a four order of magnitude improvement with
respect to the current best ground tests. Even with a further improvement of ground
results (e.g. to an accuracy of 1 part in ![]() ) space would still allow a great leap forward. In order to avoid complexity,
increase reliability and reduce cost, the whole mission design is focused on - and
optimized for - EP testing only. Therefore, it does not offer a variety of scientific
objectives as it has become the case for STEP (Worden
& Everitt, 1973; Worden, 1976; Worden, 1987; Barlier et al., 1991; Blaser et al., 1993; Blaser et al., 1994; Blaser et al., 1996) and as proposed for the
gravity mission based on the so-called SEE (Satellite Energy Exchange) method (Sanders & Deeds, 1992). In addition the
experiment is noncryogenic, the advantage being that there is no need to operate a
cryostat in space in a very delicate, small-force experiment in which perturbations from
the cryostat itself should be accurately controlled.
) space would still allow a great leap forward. In order to avoid complexity,
increase reliability and reduce cost, the whole mission design is focused on - and
optimized for - EP testing only. Therefore, it does not offer a variety of scientific
objectives as it has become the case for STEP (Worden
& Everitt, 1973; Worden, 1976; Worden, 1987; Barlier et al., 1991; Blaser et al., 1993; Blaser et al., 1994; Blaser et al., 1996) and as proposed for the
gravity mission based on the so-called SEE (Satellite Energy Exchange) method (Sanders & Deeds, 1992). In addition the
experiment is noncryogenic, the advantage being that there is no need to operate a
cryostat in space in a very delicate, small-force experiment in which perturbations from
the cryostat itself should be accurately controlled.
The main features of the mission derive from a careful analysis of ground based experiments on one side and the zero-g space environment on the other. EP experiments in the laboratory have demonstrated the advantage of rotating the torsion balance. As for vibrational noise (the analog of seismic noise on the ground), work done within the VIRGO project now under construction in Pisa has led to the development of very efficient attenuators. GG employs spinning test masses as well as mechanical suspensions. In order to reduce tidal (purely classical) gravitational perturbations, the two test masses - in the shape of hollow cylinders - are placed one inside the other. A precursor of GG, designed as a co-experiment in a multipurpose spacecraft, has appeared in 1992 (Bramanti et al., 1992) but indeed the first proposal for an EP space experiment with a spinning apparatus goes back to 1970 (Chapman & Hanson, 1970). It must be realized that an EP experiment with spinning test masses can be severely limited by centrifugal forces. An important feature of GG is that, for the first time, it exploits the effect of self-centering of bodies in supercritical rotation. It is worth stressing that, while an EP violation signal is modulated at the spin frequency, the effects of a large number of perturbing forces (e.g. due to inhomogeneities of the test bodies, spacecraft mass anomalies, nonuniform thermal expansion, parasitic capacitances, etc.) appear as DC because the entire system is spinning.
Small force gravitational experiments in space usually need to be performed inside a spacecraft equipped with thrusters in order to compensate - to some extent and in the appropriate frequency range - for the effects of the residual atmosphere and/or solar radiation acting on its external surface (and not on the test bodies inside it). However, ordinary impulsive thrusters cannot be used because they would induce vibrations of the spacecraft also at the frequency of the signal. Proportional thrusters have therefore been studied, based either on appropriate mechanical valves or on field emission electric propulsion (FEEP), but so far their in-flight performances have not been tested. Since the only scientific objective of GG is to test the equivalence principle, i.e. to detect any tiny difference in the gravitational attraction of the Earth on two bodies of equal mass and different composition, it is by definition a differential experiment. Hence, perturbations which produce the same effect on both test masses (Common Mode Effect) do not compete with the signal. If the masses are suspended (rather than free falling) any external drag effect will appear as an inertial force applied to their centres of mass and differ (for sufficiently equal masses) only because of differences in the suspension mechanisms. We have therefore devoted special care in devising a coupled suspension of the test bodies which allows us an accurate balancing and consequent reduction of the differential effects of inertial forces (Common Mode Rejection, CMR). Such a balancing would allow us to operate the experiment in non drag-free conditions, i.e. to retain entirely the perturbation from air drag (and solar radiation pressure) on the spacecraft while making small only the differential effects of the inertial forces that it generates on the suspended test bodies. Drag effects could be essentially eliminated without inducing vibrational noise were the experimental apparatus totally uncoupled from the spacecraft. This appears to be an interesting possibility in the case of a passive experimental apparatus; in fact it was proposed for measuring the universal constant of gravitation G with a miniature planet-satellite system inside an orbiting spacecraft (Nobili et al., 1990), and in general for measuring the effects of pure gravitational interaction of the test bodies (Sanders & Deeds, 1992). It is however much less attractive when dealing with an active apparatus which needs to get power from solar cells placed on the outer surface of the spacecraft and to be electrically discharged. In GG the thin springs which connect the laboratory to the spacecraft can be used for accommodating the required number of wires, and the fact of not having free floating masses avoids the build up of electrostatic charges.
In Section 2 we describe the spacecraft and the experiment. Section 3 shows, first in the framework of a simplified model and then with finite element numerical simulations, the advantages of supercritical rotation, the effect of self-centering and the concept of electrostatic active damping. Section 4 is devoted to tidal effects. The effects of inertial forces and the balancing procedure are discussed in Section 5 . Thermal effects, thermal noise and the requirements on thermal stability (to be met by passive insulation) are computed in Section 6 . The capacitance read out system is presented in Section 7 ; its sensitivity and the required level of balancing appear to be adequate for the experiment. Section 8 is devoted to showing that coupling with the higher mass moments of the test bodies from the monopole of the Earth and from nearby mass anomalies is sufficiently small. Section 9 deals with electrostatic and magnetic perturbations, reaching the conclusion that there is no need to reduce the magnetic field of the Earth inside the satellite. A procedure for locking the suspended masses during launch and properly unlocking them in orbit once the nominal spin rate has been reached is proposed in Section 10 . A preprint of this paper is available (Nobili et al., 1994).
In the present nondrag-free version of the mission the GG experiment is carried by a
small, cylindrical, spin-axis stabilized spacecraft of about 60 cm base diameter, 70 cm
height and 600 kg mass. The symmetry axis of the cylinder is, by construction, the axis of
maximum moment of inertia so as to stabilize the rotation around it. The fact of not
needing any active attitude control reduces the complexity of the mission and the
experiment (see Section 2.2 ). The spacecraft is very
compact (with an area-to-mass ratio ![]() ) in order to make the effect of non-gravitational forces, such as
air drag and solar radiation pressure, as small as possible. The orbit is almost circular,
almost equatorial at
) in order to make the effect of non-gravitational forces, such as
air drag and solar radiation pressure, as small as possible. The orbit is almost circular,
almost equatorial at ![]() altitude and
the spin axis of the satellite is almost perpendicular to the orbit plane. This maximizes
the signal and makes it unnecessary to perform any attitude manoeuvres after the initial
setup. The satellite is therefore very close to a truly passive one, which is
extremely desirable when carrying out a small force experiment. The outer surface of the
spacecraft is available for solar cells so as to generate the required power.
altitude and
the spin axis of the satellite is almost perpendicular to the orbit plane. This maximizes
the signal and makes it unnecessary to perform any attitude manoeuvres after the initial
setup. The satellite is therefore very close to a truly passive one, which is
extremely desirable when carrying out a small force experiment. The outer surface of the
spacecraft is available for solar cells so as to generate the required power.
Fig. 1. Schematic section through the spin axis of the spacecraft showing the spacecraft, the suspended laboratory and the three experimental chambers containing two test masses each. The spacecraft is a cylinder of
height and
base diameter. The figure is to scale and shows that the experiment can be performed in a very small and compact satellite (the area-to-mass ratio is
. The central chamber contains two masses made of the same (dense) material for a null test. Each of the other two chambers contains two test masses of different materials, including low density ones. The numbers 1-8 are referred to in Section 3 .
Fig. 2. Section through the spin axis of the spacecraft showing (not to scale) the spacecraft, the PGB laboratory and (for simplicity) only one experimental chamber. The PGB laboratory and the test masses are suspended with springs and their equilibrium positions can be stabilized by means of electrostatic active dampers (see Fig. 19 for a top view). The suspensions of the test masses also employ "elastic" gimbals (i.e. gimbals pivoted with torsion wires) on two movable rods for the balancing of inertial forces discussed in Section 5.2 . The axial position of each half of these rods can be finely adjusted by means of piezoelectric actuators (see also Fig. 13 ). The capacitive plates of the read out system, between the test masses, are attached to inch-worms for adjusting their distance from the surfaces of the test masses.
Inside the spacecraft it is possible to accommodate three experimental
chambers, each one carrying a couple of test masses for an EP violation experiment. Fig. 1 (to scale) shows schematically how actual test masses of ![]() each can be accommodated
inside such a satellite. However, it is easier to understand the experiment in the case of
a single experimental chamber, as shown in Fig. 2 . Vibrational noise
of the spacecraft around the spin/signal frequency is reduced by suspending the test
masses inside a low noise laboratory (also of cylindrical shape and maximum moment of
inertia with respect to the symmetry axis) which we call PGB (Pico Gravity Box).
Inside PGB a very low noise level is attained by suspending it to the spacecraft with
appropriate springs of low elastic constant
each can be accommodated
inside such a satellite. However, it is easier to understand the experiment in the case of
a single experimental chamber, as shown in Fig. 2 . Vibrational noise
of the spacecraft around the spin/signal frequency is reduced by suspending the test
masses inside a low noise laboratory (also of cylindrical shape and maximum moment of
inertia with respect to the symmetry axis) which we call PGB (Pico Gravity Box).
Inside PGB a very low noise level is attained by suspending it to the spacecraft with
appropriate springs of low elastic constant ![]() and low mechanical quality factor
and low mechanical quality factor ![]() . Thanks to weightlessness a mechanical suspension
can drastically reduce the vibrational noise of the spacecraft above a low threshold
frequency as shown in Fig. 3 .
. Thanks to weightlessness a mechanical suspension
can drastically reduce the vibrational noise of the spacecraft above a low threshold
frequency as shown in Fig. 3 .
Fig. 3. Noise reduction factor (i.e. amplitude of disturbing vibration at the suspended mass over amplitude of vibration at the suspension point) as function of frequency for a suspended laboratory of
and mechanical suspensions with stiffness
and quality factor of order 1.
and all the rest of the system (spacecraft plus test masses).
Passive mechanical suspensions in space for noise reduction in all six
degrees of freedom have been the subject of recent extensive work (Nobili et al., 1991) in particular suspensions
with low quality factor (which is very easy to obtain, e.g. with PTFE coating) in order to
eliminate the resonance peaks (Catastini et
al., 1992). The latter work gives an analytical model for longitudinal waves in a thin
bar and shows that, with low Q, resonance peaks can be abated while maintaining a
very good level of noise attenuation. Such a bar is not effective in the case of
transverse waves. However, a mechanical suspension capable to respond with comparable
stiffness in all directions (e.g. a helicoidal spring with a length comparable to its
diameter) is suitable to reduce noise in all directions. If, in addition, it has a low Q
value (for all types of deformations) it will also damp the resonance peaks. In the case
of helicoidal springs (other shapes can be suitable too) one can play with the number of
turns, their diameter, the way springs are fastened at their ends, the cross section of
the wire and the total length of the spring in order to get (for a given spring material)
the same, low, longitudinal and transversal elastic constant. If care is taken in using
suspensions which have elastic and damping constants of the same order in all directions
the analytical model used by Catastini et al.
(1992) is a good indication of what should be expected ( Catastini et al. (1992) investigate also the
problem of rotational noise showing that it is easier to deal with than the translational
one). Laboratory work performed within the VIRGO project has shown that vibrational noise
attenuation and damping can be extremely effective even in the more difficult 1-g
environment. In order to appreciate the effectiveness and simplicity of a passive noise
attenuator in space it is enough to notice that - except during the initial launch phase -
the largest acceleration on GG, which is due to friction with the residual atmosphere, is
smaller than the local gravitational acceleration on the Earth by a factor ![]() , which means that one can suspend
, which means that one can suspend ![]() in space inside the GG
spacecraft using the same (hair like) springs that one would use for suspending 0.1
milligram in a ground laboratory. Just to give an idea, an elastic constant of
in space inside the GG
spacecraft using the same (hair like) springs that one would use for suspending 0.1
milligram in a ground laboratory. Just to give an idea, an elastic constant of ![]() (both transversal and
longitudinal) is obtained with helicoidal springs a few cm long made of a few tens of
turns each one of cm size and made with a wire of about
(both transversal and
longitudinal) is obtained with helicoidal springs a few cm long made of a few tens of
turns each one of cm size and made with a wire of about ![]() diameter. If the spring is coated with PTFE - in
order to provide a low quality factor - a transfer function for vibrational noise like the
one given in Fig. 3 can be obtained. This analysis has been extended
to including the rotation of the spacecraft (Catastini
et al., 1996).
diameter. If the spring is coated with PTFE - in
order to provide a low quality factor - a transfer function for vibrational noise like the
one given in Fig. 3 can be obtained. This analysis has been extended
to including the rotation of the spacecraft (Catastini
et al., 1996).
It is important to note that the suspension springs of the PGB laboratory, besides ensuring a very low level of platform noise for the experiment, serve also other important purposes. The first is that, with no free floating masses no electrostatic charges will be able to build up anywhere inside the spacecraft. The second is to allow transferring the electric power generated by the solar cells to the experimental apparatus inside. The required number of wires can be accommodated either as independent helicoidal springs or by grouping them on a plastic support without any serious problem of degrading the reduction of vibrational noise. Once at the level of the PGB laboratory further transfer can take place through the rods and the gimbals (see Fig. 2 ).
Fig. 4. Section across the spin axes of two test bodies with their centres of mass displaced by a distance
due to an equivalence principle violation
in the field of the Earth. For
(and with mechanical properties as given in Section 3.2 ) we get
. The centres of mass of the two bodies rotate independently around
and
respectively. The direction of the displacement
changes with respect to inertial space as the satellite orbits around the Earth in
.
An EP violation in the field of the Earth results in a differential
force between the test masses in the Earth-to-satellite direction which displaces their
centres of mass to a new equilibrium where the EP violation force and the restoring force
of the suspensions balance each other. At ![]() altitude the differential acceleration of an EP violation at the level
altitude the differential acceleration of an EP violation at the level ![]() is
is ![]() . Each test body has
mass
. Each test body has
mass ![]() and is
suspended (like the PGB laboratory) by means of two springs with transversal and
longitudinal stiffness
and is
suspended (like the PGB laboratory) by means of two springs with transversal and
longitudinal stiffness ![]() (Fig. 2 ). Two rods pivoted on elastic gimbals for each
pair of test masses couple the two bodies to one another. The equivalent transverse
elastic constant, as derived from the computed natural frequencies (Section 3.2 ) is
(Fig. 2 ). Two rods pivoted on elastic gimbals for each
pair of test masses couple the two bodies to one another. The equivalent transverse
elastic constant, as derived from the computed natural frequencies (Section 3.2 ) is ![]() , hence the relative displacement caused by an EP
violation with
, hence the relative displacement caused by an EP
violation with ![]() is
is ![]() (Fig. 4 ). Since the displaced equilibrium position is fixed in the
Earth-to-satellite direction while the capacitance sensors are spinning, they will
modulate this signal at their spin frequency, namely the spin frequency of the spacecraft.
In this way the signal is displaced to a higher frequency (by several orders of magnitude)
whereby reducing the effect of
(Fig. 4 ). Since the displaced equilibrium position is fixed in the
Earth-to-satellite direction while the capacitance sensors are spinning, they will
modulate this signal at their spin frequency, namely the spin frequency of the spacecraft.
In this way the signal is displaced to a higher frequency (by several orders of magnitude)
whereby reducing the effect of ![]() noise. We choose for the spin frequency the value of
noise. We choose for the spin frequency the value of ![]() because it is large enough as compared to
the threshold frequency of the noise attenuator to guarantee very good noise reduction,
and yet reasonable for a spin-axis stabilized, small and compact satellite (note, for
instance, that the european meteorology satellites METEOSAT, whose cylindrical body is
more than 3 times bigger in height and diameter, spin at about
because it is large enough as compared to
the threshold frequency of the noise attenuator to guarantee very good noise reduction,
and yet reasonable for a spin-axis stabilized, small and compact satellite (note, for
instance, that the european meteorology satellites METEOSAT, whose cylindrical body is
more than 3 times bigger in height and diameter, spin at about ![]() ). The capacitance bridge is adequately
balanced so that common mode displacements at low frequencies, most importantly those at
the orbital frequency of the spacecraft (e.g. due to air drag) will give signals always
smaller than the differential signal expected from an EP violation (see Section 7 ). These common mode effects at low frequencies
must also be adequately rejected (see Section 5.2 )
so that their residual differential effects will not compete with the expected
signal. The fact that the entire system is spinning is extremely advantageous because it
makes all effects caused by coupling to spacecraft mass anomalies and test masses
inhomogeneities to appear as DC effects while the signal of interest is modulated at
). The capacitance bridge is adequately
balanced so that common mode displacements at low frequencies, most importantly those at
the orbital frequency of the spacecraft (e.g. due to air drag) will give signals always
smaller than the differential signal expected from an EP violation (see Section 7 ). These common mode effects at low frequencies
must also be adequately rejected (see Section 5.2 )
so that their residual differential effects will not compete with the expected
signal. The fact that the entire system is spinning is extremely advantageous because it
makes all effects caused by coupling to spacecraft mass anomalies and test masses
inhomogeneities to appear as DC effects while the signal of interest is modulated at ![]() . The only moving mass on board will be a
very limited amount of ordinary propellant which is needed only for the initial orbital
and attitude adjustments before unlocking the test masses, and for redundancy. If the
propellant is kept in a narrow toroidal tank close to the outer surface of the spacecraft,
its motion will be dominated by the centrifugal force, thus ruling out a relative motion
at the spinning frequency and therefore any interference with the signal.
. The only moving mass on board will be a
very limited amount of ordinary propellant which is needed only for the initial orbital
and attitude adjustments before unlocking the test masses, and for redundancy. If the
propellant is kept in a narrow toroidal tank close to the outer surface of the spacecraft,
its motion will be dominated by the centrifugal force, thus ruling out a relative motion
at the spinning frequency and therefore any interference with the signal.
In the GG setup, if the spin angular velocity vector ![]() is at an angle
is at an angle ![]() with respect to the orbital angular
velocity
with respect to the orbital angular
velocity ![]() of the
satellite around the Earth (
of the
satellite around the Earth (![]() ) the intensity of the differential displacement between the test masses as
seen by the rotating sensors is of the form:
) the intensity of the differential displacement between the test masses as
seen by the rotating sensors is of the form:
![]()
where ![]() is the
relative displacement of the suspended test masses in the satellite-to-Earth direction
caused by an EP violation with
is the
relative displacement of the suspended test masses in the satellite-to-Earth direction
caused by an EP violation with ![]() and
and ![]() is
the phase of the EP violation signal, which is known. The factor
is
the phase of the EP violation signal, which is known. The factor ![]() comes into play in case the
angle
comes into play in case the
angle ![]() is not zero (
is not zero (![]() is the phase angle of the
sensors with respect to the satellite-to-Earth direction). If
is the phase angle of the
sensors with respect to the satellite-to-Earth direction). If ![]() (i.e. the spin axis is exactly perpendicular
to orbit plane)
(i.e. the spin axis is exactly perpendicular
to orbit plane) ![]() , whereas for
any
, whereas for
any ![]() this factor
does reduce the intensity of the EP violation effect and introduces a dependence also on
the orbital period of the satellite. This is why the spin axis of the satellite should be
perpendicular to the orbit plane. It also leads to choosing an equatorial orbit for the
satellite.
this factor
does reduce the intensity of the EP violation effect and introduces a dependence also on
the orbital period of the satellite. This is why the spin axis of the satellite should be
perpendicular to the orbit plane. It also leads to choosing an equatorial orbit for the
satellite.
Because of the flattening of the Earth, the ascending node of a satellite orbit not
exactly equatorial would regress along the equator, i.e. the normal to the orbit plane
would describe a cone around the normal to the equator. The spin axis of the satellite, if
not exactly normal to the orbit would in turn precess around the normal to the orbit
because of the effect of the Earth's monopole on a body - the satellite - with different
principal moments of inertia. Thus, even if the spin axis and the normal to the orbit were
originally aligned, they would no longer be so after a few tens of days. Attitude
manoeuvres would then be necessary to realign the spin axis to the orbit normal in order
to have a factor ![]() in Eq. 2 , hence to maximize the effect of an EP violation. This may require
to activate the locking-unlocking device (Section 10 ),
which would complicate the mission. Instead, if the satellite is originally injected in an
orbit close to equatorial with the spin axis close to the normal to it, the spin axis and
the orbit normal will stay close to one another (by the same amount) and attitude
manoeuvres will not be required. In addition to that, the equatorial orbit has - if low
enough - the advantage of avoiding the perturbing effects of the radiation from the Van
Allen belts in the so-called South Atlantic Anomaly. An altitude of
in Eq. 2 , hence to maximize the effect of an EP violation. This may require
to activate the locking-unlocking device (Section 10 ),
which would complicate the mission. Instead, if the satellite is originally injected in an
orbit close to equatorial with the spin axis close to the normal to it, the spin axis and
the orbit normal will stay close to one another (by the same amount) and attitude
manoeuvres will not be required. In addition to that, the equatorial orbit has - if low
enough - the advantage of avoiding the perturbing effects of the radiation from the Van
Allen belts in the so-called South Atlantic Anomaly. An altitude of ![]() is suitable for this purpose. We therefore
assume an equatorial, low eccentricity orbit at
is suitable for this purpose. We therefore
assume an equatorial, low eccentricity orbit at ![]() altitude and allow for an angle of a few degrees between the spin axis and
the normal to the orbit plane as well as the inclination of the orbit on the equator,
which are rather relaxed constraints for orbit injection. In this configuration no active
control is needed, neither of the attitude nor of the orbit.
altitude and allow for an angle of a few degrees between the spin axis and
the normal to the orbit plane as well as the inclination of the orbit on the equator,
which are rather relaxed constraints for orbit injection. In this configuration no active
control is needed, neither of the attitude nor of the orbit.
The satellite should be equipped with ordinary star trackers or Earth
elevation sensors in order to monitor its spin rate and its instantaneous orientation.
Although a predetermined spinning frequency is not needed, a knowledge of the actual spin
rate or, more precisely, of the angle ![]() at all times, is required in the process of data analysis for
removing small perturbations close to the signal frequency (Section 5.3 ), for checking purposes and to provide the
electrostatic damper with a reference signal synchronized to the spin (Section 3.1 ). For communication with the Earth several
choices are possible (see GALILEO GALILEI,
1996); a despun antenna should be avoided because moving parts would disturb the
experiment. Since the orbit is low and equatorial the satellite will be in view of the
ground station only for a fraction of its orbital period. There is no special need for
continuous tracking; the experimental data can be stored on board and down loaded once per
orbit. The required bit rate is low.
at all times, is required in the process of data analysis for
removing small perturbations close to the signal frequency (Section 5.3 ), for checking purposes and to provide the
electrostatic damper with a reference signal synchronized to the spin (Section 3.1 ). For communication with the Earth several
choices are possible (see GALILEO GALILEI,
1996); a despun antenna should be avoided because moving parts would disturb the
experiment. Since the orbit is low and equatorial the satellite will be in view of the
ground station only for a fraction of its orbital period. There is no special need for
continuous tracking; the experimental data can be stored on board and down loaded once per
orbit. The required bit rate is low.
While moving around the Earth the test masses will also orbit, together with the
planet, around the Sun. Therefore, the equivalence between inertial and gravitational mass
can also be tested by comparing the gravitational attraction of the Sun with the
centrifugal force due to the orbital motion around it. In this case the acceleration of an
EP violation is ![]() ,
with
,
with ![]() the mass of
the Sun acting at its distance from the satellite (in practice the Earth-Sun
distance
the mass of
the Sun acting at its distance from the satellite (in practice the Earth-Sun
distance ![]() ,
namely
,
namely ![]() ), and
), and ![]() the Eötvös parameter
expressing the violation of the equivalence between inertial and gravitational mass for
the test masses in the field of the Sun. Since
the Eötvös parameter
expressing the violation of the equivalence between inertial and gravitational mass for
the test masses in the field of the Sun. Since ![]() , while
, while ![]() it is apparent that our experimental apparatus
cannot detect an EP violation due to the Sun to the same accuracy as for the Earth. We
shall have
it is apparent that our experimental apparatus
cannot detect an EP violation due to the Sun to the same accuracy as for the Earth. We
shall have ![]() . For
instance, if the experiment is limited to
. For
instance, if the experiment is limited to ![]() , an EP violation due to the Sun can be tested to
, an EP violation due to the Sun can be tested to ![]() , which would be better than
achieved on Earth so far. The signal on the sensors will have a frequency which differs
from that of an EP violation signal in the field of the Earth by the orbital frequency of
the satellite. It will also be modulated by the annual motion of the Earth around the Sun.
The two frequencies, from the Sun and from the Earth, can therefore be distinguished.
, which would be better than
achieved on Earth so far. The signal on the sensors will have a frequency which differs
from that of an EP violation signal in the field of the Earth by the orbital frequency of
the satellite. It will also be modulated by the annual motion of the Earth around the Sun.
The two frequencies, from the Sun and from the Earth, can therefore be distinguished.
Similarly, one can analyze the data searching for possible violations of the equivalence principle driven by other sources such as the galaxy. Naturally, the sensitivity that can be achieved will depend on the intensity of the driving signal in each case, which however for the Sun and other sources farther away will be the same as it is on the ground. Indeed, all efforts towards more sensitive ground apparata for testing the equivalence principle should be strongly encouraged because their contribution is unique at short range and very valuable over distances much bigger than the radius of the Earth.
An experiment which aims at testing the equivalence principle must be capable to detect
tiny relative displacements of the test masses with respect to one another. However,
spurious relative motions would appear, because of gravity gradients, were the centres of
mass of the test bodies not accurately centred on one another. This is why the test masses
must be concentric, as they are in STEP. In GG their cylindrical shape is not only a
construction advantage; it is clearly dictated by the symmetry of the one axis rotation.
The crucial question is: how, and to what accuracy, is mass centering obtained? The answer
comes from a careful exploitation of weightlessness, which makes the mechanical system
(spacecraft, PGB and test masses) a rotor in supercritical rotation with the spin
frequency ![]() much larger than the
natural oscillation frequency
much larger than the
natural oscillation frequency ![]() of the suspended test masses (and the PGB laboratory as well). Since the end
of last century such rotors are known to have an equilibrium position very close to the
rotation axis, which is pivotal in reducing the otherwise destructive effects of
centrifugal forces in high-speed machines such as turbines, centrifuges and ultra-vacuum
pumps (see Whitley (1984) for a review). In
simple terms, the rotor tends to spin around its centre of mass, i.e. it behaves more like
a free rotor rather than a constrained one. If the centre of mass of the suspended body is
located, by construction, at a distance
of the suspended test masses (and the PGB laboratory as well). Since the end
of last century such rotors are known to have an equilibrium position very close to the
rotation axis, which is pivotal in reducing the otherwise destructive effects of
centrifugal forces in high-speed machines such as turbines, centrifuges and ultra-vacuum
pumps (see Whitley (1984) for a review). In
simple terms, the rotor tends to spin around its centre of mass, i.e. it behaves more like
a free rotor rather than a constrained one. If the centre of mass of the suspended body is
located, by construction, at a distance ![]() from the rotation axis, equilibrium is established on the opposite side
of
from the rotation axis, equilibrium is established on the opposite side
of ![]() with respect to the rotation
axis, where the centrifugal force due to rotation and the restoring elastic force of the
suspension equal each other. It can be shown that this happens at a distance from the spin
axis smaller than the original unbalance
with respect to the rotation
axis, where the centrifugal force due to rotation and the restoring elastic force of the
suspension equal each other. It can be shown that this happens at a distance from the spin
axis smaller than the original unbalance ![]() by a factor
by a factor ![]() (see, e.g., Ch. 6 of Den Hartog, 1985).
Thus, at equilibrium, the distance
(see, e.g., Ch. 6 of Den Hartog, 1985).
Thus, at equilibrium, the distance ![]() of each suspended test mass inside the GG satellite from the spin
axis - and therefore from one another - is:
of each suspended test mass inside the GG satellite from the spin
axis - and therefore from one another - is:
![]()
Since the pioneer work of Gustaf De Laval about a century ago this relationship has been
widely demonstrated in both theoretical and experimental work on high speed rotors. It
shows that space offers an important advantage, because in absence of weight the natural
frequencies of suspended bodies can be very low, about ![]() smaller that the spin frequency in this case. For an original
unbalance
smaller that the spin frequency in this case. For an original
unbalance ![]() this means that the
equilibrium position is only
this means that the
equilibrium position is only ![]() away
from the spin axis. It is important to stress that this equilibrium position slightly
displaced from the rotation axis is fixed in the rotating frame of the spacecraft while
the signal is modulated at the frequency of spin. Possible imperfections on the surfaces
of the bodies would also give a DC effect. The actual direction of the miscentering in the
rotating system depends only upon the location of the unbalance and is of no importance
for the experiment. Perturbations such as air drag and solar radiation pressure acting on
the external surface of the spacecraft produce a nongravitational acceleration of its
centre of mass. In the reference frame of the spacecraft the bodies will therefore be
subject to inertial forces in the opposite direction, which will move the masses to new
displaced positions of equilibrium (along the direction of the perturbation) where the
perturbation is balanced by the restoring force of the spring. It is worth noticing that,
because of the supercritical state of rotation, the displaced body will always spin around
its own axis, which means that no centrifugal force due to the spin will result because of
this displacement. The only centrifugal forces due to the spin come from the
away
from the spin axis. It is important to stress that this equilibrium position slightly
displaced from the rotation axis is fixed in the rotating frame of the spacecraft while
the signal is modulated at the frequency of spin. Possible imperfections on the surfaces
of the bodies would also give a DC effect. The actual direction of the miscentering in the
rotating system depends only upon the location of the unbalance and is of no importance
for the experiment. Perturbations such as air drag and solar radiation pressure acting on
the external surface of the spacecraft produce a nongravitational acceleration of its
centre of mass. In the reference frame of the spacecraft the bodies will therefore be
subject to inertial forces in the opposite direction, which will move the masses to new
displaced positions of equilibrium (along the direction of the perturbation) where the
perturbation is balanced by the restoring force of the spring. It is worth noticing that,
because of the supercritical state of rotation, the displaced body will always spin around
its own axis, which means that no centrifugal force due to the spin will result because of
this displacement. The only centrifugal forces due to the spin come from the ![]() miscentering given by Eq. 3 and are balanced by the restoring force of the suspension springs.
miscentering given by Eq. 3 and are balanced by the restoring force of the suspension springs.
It is however well known that any rotating system operating in the supercritical regime is unstable - owing to its internal damping - unless an adequate "non-rotating damping" is applied to it, that is damping caused by friction of the non rotating - or slowly rotating - parts of the bearings (on which the spinning shaft is mounted) against their supports. See Bramanti et al. (1996), Nobili et al. (1996) for an analysis of the various types of friction. Since the spacecraft as a whole is rotating, there is no way of obtaining the required non-rotating damping except by increasing the complexity of the system with the introduction of a fixed or slowly rotating portion of it. A simpler solution is to place in between the various masses active elements able to simulate the behaviour of a non-rotating damper. In the language of automotive active suspension technology the device can be defined as a "skyhook damper" since it acts as a damper which in a way follows an inertial reference frame. In Section 3.1 we show the main properties of supercritical rotation and the rôle of internal and non-rotating damping in a simplified mathematical model of two masses connected with springs; then report the results of a finite element numerical simulation of the system in the 3-chamber setup of Fig. 1 , giving all the unstable whirling modes of the system and showing how they are damped (Section 3.2 ). The electrostatic damper is discussed in Section 3.3 .
Unlike GG, the STEP experiment has been based on the fact that its
attitude be actively maintained fixed with respect to inertial space as well as drag-free
(in angle) to a level compatible with the requirement on orbital drag-free, which turns
out to be a very demanding requirement. In this way, with a considerable effort in
accurate active control, an EP violation signal from the Earth would appear at the
satellite orbital frequency (![]() ).
However, since the signal frequency is the frequency of orbital motion around the Earth it
is bound to be also the frequency of a number of dangerous perturbing effects (e.g from
the South Atlantic Anomaly and from the on board Helium used to make the experiment
cryogenic). More recently it has been proposed that the STEP spacecraft be spinning too,
but only slightly faster than its orbital revolution around the Earth. The benefits of
fast satellite spin could not be incorporated either in the first proposed rotating
experiment (Chapman & Hanson, 1970). In
that experiment centrifugal forces remain a major limitation because the test bodies are
constrained to move along one diameter of the rotating platform, and it is well known that
any such rotating system is always strongly unstable above the critical speed (Ch. 6, p.
228 of Den Hartog, 1985).
).
However, since the signal frequency is the frequency of orbital motion around the Earth it
is bound to be also the frequency of a number of dangerous perturbing effects (e.g from
the South Atlantic Anomaly and from the on board Helium used to make the experiment
cryogenic). More recently it has been proposed that the STEP spacecraft be spinning too,
but only slightly faster than its orbital revolution around the Earth. The benefits of
fast satellite spin could not be incorporated either in the first proposed rotating
experiment (Chapman & Hanson, 1970). In
that experiment centrifugal forces remain a major limitation because the test bodies are
constrained to move along one diameter of the rotating platform, and it is well known that
any such rotating system is always strongly unstable above the critical speed (Ch. 6, p.
228 of Den Hartog, 1985).
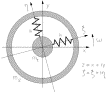
Fig. 5. A mathematical model of two axially symmetric bodies of masses
and
coupled by springs of stiffness k.
and
are the inertial and the rotating plane respectively. z and
are the complex variables in the two planes.
Let us first study the system in the simplified model of two
axisymmetrical rigid bodies of masses ![]() and
and ![]() , length
, length ![]() , moments of
inertia
, moments of
inertia ![]() and
and ![]() with respect to their
symmetry (polar) axis and
with respect to their
symmetry (polar) axis and ![]() ,
, ![]() with
respect to any transversal axis x, y. The bodies are coupled by two
identical springs, each of radial stiffness k as shown in Fig. 5 .
By introducing the complex coordinates
with
respect to any transversal axis x, y. The bodies are coupled by two
identical springs, each of radial stiffness k as shown in Fig. 5 .
By introducing the complex coordinates ![]() and
and ![]() , where
, where ![]() and
and ![]() are the
rotation angles around the y and x axes (the minus sign allows to simplify
the metrical form of the equations), the equation of motion for the lateral dynamics of
the system is (Section 4.6 of Genta, 1993):
are the
rotation angles around the y and x axes (the minus sign allows to simplify
the metrical form of the equations), the equation of motion for the lateral dynamics of
the system is (Section 4.6 of Genta, 1993):
![]()
where
![]()
is the vector of the generalized coordinates of the system (subscripts 1 and 2 distinguish
the two bodies) and ![]() ,
, ![]() ,
, ![]() are known as the mass,
gyroscopic and stiffness matrices:
are known as the mass,
gyroscopic and stiffness matrices:
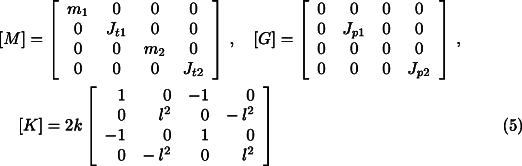
Because of possible construction errors each body will have the centre of gravity located
a distance ![]() away from its rotation
axis, and the symmetry axis tilted by an angle
away from its rotation
axis, and the symmetry axis tilted by an angle ![]() with respect to its rotation axis. These unbalances
will result in the forcing terms at the right hand side of the equation of motion (Eq. 4 ) which contain the vector
with respect to its rotation axis. These unbalances
will result in the forcing terms at the right hand side of the equation of motion (Eq. 4 ) which contain the vector ![]()
![]()
where ![]() defines the direction of the
vector
defines the direction of the
vector ![]() in the rotating frame
and
in the rotating frame
and ![]() is the phase
angle of the couple due to the unbalance. In the general case of the Jeffcott rotor (Jeffcott, 1919) the system is subject to
nonconservative forces (damping forces) which can be of two kinds: either of fixed
direction in the inertial frame (non-rotating damping) or of fixed direction in the
rotating frame (rotating damping). The latter occurs in the parts of the system which spin
at speed
is the phase
angle of the couple due to the unbalance. In the general case of the Jeffcott rotor (Jeffcott, 1919) the system is subject to
nonconservative forces (damping forces) which can be of two kinds: either of fixed
direction in the inertial frame (non-rotating damping) or of fixed direction in the
rotating frame (rotating damping). The latter occurs in the parts of the system which spin
at speed ![]() (e.g. the springs), while
the former is linked with the nonrotating parts of the machine. They are usually expressed
as matrices
(e.g. the springs), while
the former is linked with the nonrotating parts of the machine. They are usually expressed
as matrices ![]() and
and ![]() respectively,
with
respectively,
with ![]() the total
damping matrix of the system. In the case of GG the entire system is spinning and
therefore there is no non-rotating damping, i.e.
the total
damping matrix of the system. In the case of GG the entire system is spinning and
therefore there is no non-rotating damping, i.e. ![]() and
and ![]() . The matrix
. The matrix ![]() is given by:
is given by:
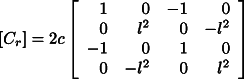
where c is the damping coefficient. For internal hysteretic damping the value of c,
for the translational modes, can be approximated as ![]() , with Q the quality factor and
, with Q the quality factor and ![]() .
.
Because of symmetry Eq. 4 can be split into two different sets of uncoupled equations, one for the translational modes
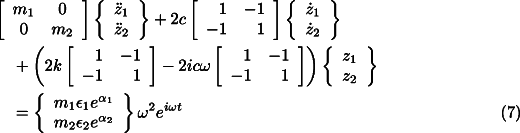
and one for the rotational modes
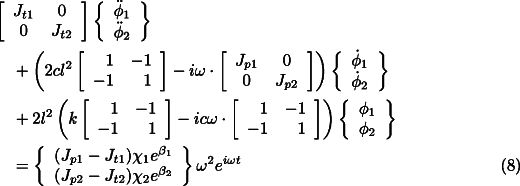
Let us consider the equation for the translational dynamics of the system (Eq.
7 ). Assuming a solution of the type ![]() for the free whirling, the characteristic equation of the
homogeneous system is
for the free whirling, the characteristic equation of the
homogeneous system is
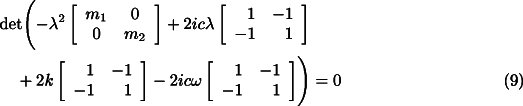
whose solutions (i.e. the complex frequencies of the system) are 0 and the solutions of
the equation:
![]()
which is the characteristic equation of a Jeffcott rotor with mass ![]() in the absence of
non-rotating damping. It is well known that this device is unstable at all speeds
exceeding the critical speed (see, e.g., 4.8.3 of Genta,
1993)
in the absence of
non-rotating damping. It is well known that this device is unstable at all speeds
exceeding the critical speed (see, e.g., 4.8.3 of Genta,
1993)

Thus, without non-rotating damping operation in supercritical regime (i.e. above the
critical speed) is not possible because the rotor is necessarily unstable. From a more
physical point of view, the springs - because of their internal dissipation - will
necessarily transfer the spin angular momentum of each body to their rotational motion
around one another, giving rise, in the inertial reference frame, to a circular forward
motion of increasing amplitude of each axial end of the rotation axis of each body around
the equilibrium position. There is a cylindrical whirl if the two ends move in phase and a
conical (also called precessional) one if they move ![]() out of phase. The natural position of equilibrium with the two
axes very accurately aligned still exists but whirling motions around it necessarily grow
in time, inevitably bringing the system to instability. It is worth stressing that if the
suspension springs are very tiny, with very low stiffness k and relatively high Q
values, the timescales of these instabilities are large, as numerical simulations confirm
(Section 3.2 ). This is very important in devising an
efficient active damper.
out of phase. The natural position of equilibrium with the two
axes very accurately aligned still exists but whirling motions around it necessarily grow
in time, inevitably bringing the system to instability. It is worth stressing that if the
suspension springs are very tiny, with very low stiffness k and relatively high Q
values, the timescales of these instabilities are large, as numerical simulations confirm
(Section 3.2 ). This is very important in devising an
efficient active damper.
Non-rotating damping can be simulated by an active device which exerts
on the mass ![]() a force
a force
![]()
where ![]() is the
overall gain of the device and
is the
overall gain of the device and ![]() is the complex displacement measured in the rotating reference frame
is the complex displacement measured in the rotating reference frame ![]()
![]() as shown in Fig.
5 . The device exerts a force of the same intensity and direction but opposite sign on
the mass
as shown in Fig.
5 . The device exerts a force of the same intensity and direction but opposite sign on
the mass ![]() . In the
inertial reference frame
. In the
inertial reference frame ![]() the equation of motion of the system is now given by Eq. 4 by
adding the term
the equation of motion of the system is now given by Eq. 4 by
adding the term
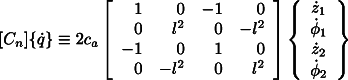
to its left hand side. Assuming again a solution of the type ![]() for the free whirling, the
characteristic equation of the homogeneous system for translational motions is
for the free whirling, the
characteristic equation of the homogeneous system for translational motions is
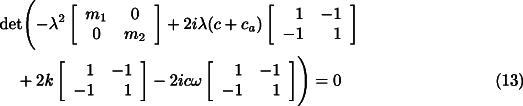
whose solutions are 0 and the solutions of the equation:
![]()
which is the characteristic equation of a Jeffcott rotor with mass ![]() , non-rotating damping
, non-rotating damping ![]() and rotating damping c.
It is well known that this device is stable at all speeds below the maximum value
and rotating damping c.
It is well known that this device is stable at all speeds below the maximum value ![]()
![]()
It follows that rotation at supercritical speed ![]() which were to ensure very good centering (i.e.
which were to ensure very good centering (i.e. ![]() ) as well as stability necessarily requires
) as well as stability necessarily requires ![]() . The case of the test masses
in the GG satellite is a very favourable one because the tiny suspension springs have very
low internal damping c due to the very low stiffness k and relatively high Q.
Hence a small amount of active damping
. The case of the test masses
in the GG satellite is a very favourable one because the tiny suspension springs have very
low internal damping c due to the very low stiffness k and relatively high Q.
Hence a small amount of active damping ![]() is sufficient to guarantee stability even at a spin
frequency
is sufficient to guarantee stability even at a spin
frequency ![]() much larger than the
critical frequency
much larger than the
critical frequency ![]() .
Thus, the active dampers are neither required to provide large forces nor to operate with
small response times, since the unstable modes of the rotor are characterized by low
frequencies (see Section 3.2 ). The nice fact about
supercritical rotation is that the equilibrium position, with the axes closely aligned, is
a physical property of the system and unstable rotational motions around this equilibrium
position take place very slowly. This makes relatively easy centering to the position of
equilibrium by means of active damping, clearly much easier than it would be in absence of
such a naturally provided position of equilibrium. In Section
3.3 we present an electrostatic damper that appears to be suitable for our purposes.
Here we wish to stress that in the rotating reference frame (to which the electrostatic
plates of the damper are attached as shown in Fig. 2 ) it must supply
a force with components:
.
Thus, the active dampers are neither required to provide large forces nor to operate with
small response times, since the unstable modes of the rotor are characterized by low
frequencies (see Section 3.2 ). The nice fact about
supercritical rotation is that the equilibrium position, with the axes closely aligned, is
a physical property of the system and unstable rotational motions around this equilibrium
position take place very slowly. This makes relatively easy centering to the position of
equilibrium by means of active damping, clearly much easier than it would be in absence of
such a naturally provided position of equilibrium. In Section
3.3 we present an electrostatic damper that appears to be suitable for our purposes.
Here we wish to stress that in the rotating reference frame (to which the electrostatic
plates of the damper are attached as shown in Fig. 2 ) it must supply
a force with components:
![]()
Thus, since the effect produced by the damper must be at the frequency of the whirling
motions, the unstable ones being at the (slow) natural frequency of oscillation, the
damper must actuate at the spin frequency minus the natural one, which is different from
the frequency of an EP violation. For the electrostatic plates to be able to recover and
damp the slow velocity of whirl while spinning much faster, the control software must be
able to subtract away their own velocity of spin, and this requires that either star
trackers or Earth elevation sensors provide a reference signal synchronized with the spin.
(For a detailed discussion on unstable whirl motions and active rotating damping in space
see Bramanti et al., 1996; GALILEO GALILEI, 1997; Nobili et al., 1996).
Fig. 6. Sketch of the FEM (Finite Element Method) model of GG. The figure shows the final FEM model used to analyse the rotordynamics of the active controlled system with DYNROT. The beam elements have been drawn on the left side of the picture: the white parts correspond to zero mass beams with structural stiffness. The nodes are shown on the right side of the sketch, each node corresponding to two translational and two rotational degrees of freedom which describe the lateral dynamics. In order to provide an understandable overview each node has been located on the corresponding beam element, instead of on the rotation axis of the satellite, as it actually is. Since each active damper has been connected to the central rod there are shorter beam elements near the gimbals and two nodes very close to each other.
Fig. 7. Schematic representation of the various components of one experimental chamber placed next to one another in order to show the different kind of connections between them (springs, gimbals and electrostatic dampers). The outer and the inner test mass are respectively connected by spring elements (continuous line) to the pair of movable supports. Gimbals join the movable supports to the central rod, while the electrostatic dampers act between the test masses and the central rod (dotted line).
A more realistic model was built using the finite element
rotordynamics code DYNROT, developed over the years at the Department of Mechanics of
"Politecnico di Torino". The model, which includes the satellite body, the PGB
laboratory and three pairs of test masses, is shown in Fig. 1 where
the numbers 1-8 distinguish the various components of the system for later reference. The
test masses are connected to the PGB by very low stiffness springs and movable supports
with elastic gimbals at their midpoints as shown in Fig. 2 . We first
compute the whirling modes of the system assuming that no active dampers are present. The
model consists of 36 beam elements and 20 spring elements (see Fig. 6 ,
Fig. 7 ). A number of beam elements which is larger than the minimum
necessary to model the 8 cylindrical bodies and the central rod with movable supports has
been used in order to allow us to define the location of the attachment points of the
springs. The stiffness of the beam elements is orders of magnitude larger than that of the
springs, so that they behave as rigid bodies in the whole frequency range of interest.
Beam elements have been chosen instead of concentrated mass elements in order to use the
ability of the code to compute directly the inertial properties from the geometrical
parameters. Once the model was built, the number of degrees of freedom was reduced from 98
complex degrees of freedom, related to the displacements and rotations of all 49 nodes, to
16 through Guyan reduction (see, e.g., Section 2.8 of Genta,
1993). The minimum number of degrees of freedom necessary to define rigid-body motion
was chosen, thus ensuring that no deflection of the beam elements can occur. The inertial
properties of the rigid bodies are listed in Table 1 , where the
numbers 1-8 refer to the various parts of the system as shown in Fig. 1 .
The ratio ![]() is also
listed. The masses of the central rod and of the movable supports have been neglected. The
code was run using the same stiffness of
is also
listed. The masses of the central rod and of the movable supports have been neglected. The
code was run using the same stiffness of ![]() , both longitudinal and transversal, for all the springs (2 for
each body) and the same torsional constant
, both longitudinal and transversal, for all the springs (2 for
each body) and the same torsional constant ![]() , for all the elastic gimbals (2 for each pair of test masses).
This value can be obtained if the diameter of the wires in the gimbals is about
, for all the elastic gimbals (2 for each pair of test masses).
This value can be obtained if the diameter of the wires in the gimbals is about ![]() and their length from
and their length from ![]() to
to ![]() . The stiffness of the springs is relevant in response to forces in
common mode while the gimbals enter into play when a pair of coupled test masses is
subject to a differential force, resulting in an equivalent transverse stiffness
. The stiffness of the springs is relevant in response to forces in
common mode while the gimbals enter into play when a pair of coupled test masses is
subject to a differential force, resulting in an equivalent transverse stiffness ![]() (l is the length of
the rod from the gimbal to the spring, that is the arm; l is between
(l is the length of
the rod from the gimbal to the spring, that is the arm; l is between ![]() and
and ![]() in the 3-chamber model of Fig. 1 ). The
resulting equivalent transverse stiffness are therefore not exactly the same, but they are
all smaller than the
in the 3-chamber model of Fig. 1 ). The
resulting equivalent transverse stiffness are therefore not exactly the same, but they are
all smaller than the ![]() stiffness of the springs. In the code the system is simplified in that either the springs
or the gimbals respond, depending on whether the motion is in common mode (both masses
together) or in differential mode (one mass with respect to the other) respectively. While
it is true that the gimbals do not affect common mode motions, the springs play a rôle
also in differential motions. However, they respond to differential deformations with a
lower elastic constant (the bending constant) than they do in the case of transversal
common mode deformations. How much smaller is computed by Den Hartog (Appendix, p. 429 of Den Hartog, 1985), for a beam, and the numerical
factor is 4. In laboratory tests with helicoidal springs we have measured a factor 3. Each
pair of suspended test bodies will therefore have a lower natural frequency for
oscillations in differential mode and a higher one for those in common mode:
stiffness of the springs. In the code the system is simplified in that either the springs
or the gimbals respond, depending on whether the motion is in common mode (both masses
together) or in differential mode (one mass with respect to the other) respectively. While
it is true that the gimbals do not affect common mode motions, the springs play a rôle
also in differential motions. However, they respond to differential deformations with a
lower elastic constant (the bending constant) than they do in the case of transversal
common mode deformations. How much smaller is computed by Den Hartog (Appendix, p. 429 of Den Hartog, 1985), for a beam, and the numerical
factor is 4. In laboratory tests with helicoidal springs we have measured a factor 3. Each
pair of suspended test bodies will therefore have a lower natural frequency for
oscillations in differential mode and a higher one for those in common mode: ![]() and
and ![]() (where
(where ![]() is the equivalent transverse
stiffness and k the stiffness of each spring;
is the equivalent transverse
stiffness and k the stiffness of each spring; ![]() because there are two springs for each mass and m because
the reduced mass between the test mass m and the rest of the spacecraft is
essentially m). A factor about 2 between these frequencies is reasonable to obtain,
and this is the situation simulated with the DYNROT code.
because there are two springs for each mass and m because
the reduced mass between the test mass m and the rest of the spacecraft is
essentially m). A factor about 2 between these frequencies is reasonable to obtain,
and this is the situation simulated with the DYNROT code.
Table 1. Inertial properties of the rigid bodies (as numbered in Fig. 1) which constitute the FEM model
Fig. 8. Mode shapes of GG satellite. The mode shapes found by the DYNROT FEM code can be divided into three types: the first includes 7 cylindrical modes forward and backward, the second 7 backward mainly conical modes and the third 8 conical forward modes. A sample of each set including the
and
forward modes and the
backward mode is shown by giving the position of the axis of rotation (continuous line) and the location of the nodes (the "
" symbols). The x-
is a coordinate along the spacecraft axis (in cm); the y-
is an adimensional normalized coordinate (the mode automatically scales all the modes to the maximum value).
The frequencies of free whirling are computed for the spacecraft spin
rate ![]() . Apart from the zero
frequency modes, we find (in
. Apart from the zero
frequency modes, we find (in ![]() ): a
set of 7 backward mainly conical whirling modes of frequencies
): a
set of 7 backward mainly conical whirling modes of frequencies ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ; a set of 7 cylindrical modes, forward and
backward of frequencies
; a set of 7 cylindrical modes, forward and
backward of frequencies ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ; a set of 8
conical forward whirling modes of frequencies
; a set of 8
conical forward whirling modes of frequencies ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() close to the spin
frequency. A graphical representation for some of the computed modes is given in Fig. 8 . With the introduction of some internal damping of the springs
which suspend the test masses (e.g.
close to the spin
frequency. A graphical representation for some of the computed modes is given in Fig. 8 . With the introduction of some internal damping of the springs
which suspend the test masses (e.g. ![]() it is found that only the forward cylindrical modes become
unstable, and the e-folding times are a few
it is found that only the forward cylindrical modes become
unstable, and the e-folding times are a few ![]() (all other modes are naturally damped). As expected, instabilities are there
but they build up slowly. As for the PGB laboratory the timescales for instability are
shorter because, although the mass is bigger than that of the test bodies, the quality
factor
(all other modes are naturally damped). As expected, instabilities are there
but they build up slowly. As for the PGB laboratory the timescales for instability are
shorter because, although the mass is bigger than that of the test bodies, the quality
factor ![]() of its
springs is smaller. Note that all modes with eigenfrequencies close to the
spin/signal frequency are conical (i.e. angular precessions), not cylindrical modes, which
means that they do not affect the centre of mass of the bodies whose relative displacement
is the observable in this experiment. Moreover, it is well known and the simulations
confirm it, that they are naturally damped, i.e they are not unstable. We can conclude
that there is no interference between these modes and the signal. As for the frequencies
of the 7 cylindrical modes listed above (both forward and backward, the forward ones being
those which become unstable in the presence of a nonzero internal damping of the springs)
we note that they are the eigenfrequencies of the suspended bodies (two for each pair of
test masses plus one for the PGB laboratory) as they have been computed in the numerical
simulation of the 3-chamber system. As a matter of fact, since we study the mechanical
system as a whole these are the natural frequencies of the system; however, due to
the weakness of the springs, they can be still recognized as due to the various suspended
masses. In order to avoid mutual mechanical influences between the three pairs of masses
it is sufficient that their frequencies be separated by a few times their bandwidths. In
this simulation in which all the springs have a stiffness of
of its
springs is smaller. Note that all modes with eigenfrequencies close to the
spin/signal frequency are conical (i.e. angular precessions), not cylindrical modes, which
means that they do not affect the centre of mass of the bodies whose relative displacement
is the observable in this experiment. Moreover, it is well known and the simulations
confirm it, that they are naturally damped, i.e they are not unstable. We can conclude
that there is no interference between these modes and the signal. As for the frequencies
of the 7 cylindrical modes listed above (both forward and backward, the forward ones being
those which become unstable in the presence of a nonzero internal damping of the springs)
we note that they are the eigenfrequencies of the suspended bodies (two for each pair of
test masses plus one for the PGB laboratory) as they have been computed in the numerical
simulation of the 3-chamber system. As a matter of fact, since we study the mechanical
system as a whole these are the natural frequencies of the system; however, due to
the weakness of the springs, they can be still recognized as due to the various suspended
masses. In order to avoid mutual mechanical influences between the three pairs of masses
it is sufficient that their frequencies be separated by a few times their bandwidths. In
this simulation in which all the springs have a stiffness of ![]() and all the gimbals have a
torsional constant of
and all the gimbals have a
torsional constant of ![]() the DYNROT code provides: a frequency of about
the DYNROT code provides: a frequency of about ![]() to be associated with the oscillations of
the PGB and corresponding to an elastic constant
to be associated with the oscillations of
the PGB and corresponding to an elastic constant ![]() ; three frequencies between
; three frequencies between ![]() and
and ![]() to be associated with the differential modes; three higher
frequencies between
to be associated with the differential modes; three higher
frequencies between ![]() and
and ![]() to be associated with the common modes. From
now on we use
to be associated with the common modes. From
now on we use ![]() for the common mode
and
for the common mode
and ![]() for the differential mode,
noticing that there is enough liberty in the choice of the springs and gimbals to actually
obtain these values. The corresponding elastic constants are:
for the differential mode,
noticing that there is enough liberty in the choice of the springs and gimbals to actually
obtain these values. The corresponding elastic constants are: ![]() , for the response to forces
in differential mode and
, for the response to forces
in differential mode and ![]() for the response of each mass to forces in common mode. The fact of having a
good separation between the eigenfrequencies in common mode and those in differential mode
(the latter being smaller) is very useful because in this way displacements in response to
perturbations in common mode (air drag) are reduced while those in differential mode (EP
violation) are increased.
for the response of each mass to forces in common mode. The fact of having a
good separation between the eigenfrequencies in common mode and those in differential mode
(the latter being smaller) is very useful because in this way displacements in response to
perturbations in common mode (air drag) are reduced while those in differential mode (EP
violation) are increased.
At this point we insert into the model a set of ideal active dampers
providing the force (Eq. 16 ). In doing so we also refine the model
by increasing the number of elements to 82 (48 beam elements, 20 spring elements and 14
active dampers). The model includes 61 nodes and the number of degrees of freedom is
reduced from 122 complex degrees to 16 through Guyan reduction. We assume a gain of ![]() for all the 12 elements
damping the test masses. It is found that all unstable modes become stable and the
timescales for damping are of 1 to 10 hours. For details on the physics of unstable whirl
motions and their active control with rotating electrostatic dampers see Bramanti et al. (1996), GALILEO GALILEI (1997), Nobili et al. (1996).
for all the 12 elements
damping the test masses. It is found that all unstable modes become stable and the
timescales for damping are of 1 to 10 hours. For details on the physics of unstable whirl
motions and their active control with rotating electrostatic dampers see Bramanti et al. (1996), GALILEO GALILEI (1997), Nobili et al. (1996).
Fig. 9. Electrostatic damping of whirling motions. The circular instability motions of the rotation axis of the inner shaft, which have the natural (low) frequency of the suspended masses
, can be actively damped by means of the electrostatic force obtained by applying a voltage pulse V of short duration (for example for about one fourth of the spin period, i.e. about
) to each plate rotating at the (rapid) spin frequency
when it is passing through the position
before the point of its nearest approach to the inner shaft. This happens, for each plate, at a frequency which is equal to the spin frequency
minus the natural frequency
.
The force acting between the two elements of the electrostatic damper (Fig. 9 ) for an assumed voltage V is (in MKS):
![]()
with S the surface of the actuator and x the gap between the equipotential
surfaces of the damper. For small displacements and tensions the force can be linearized
around a constant voltage ![]() and reference gap
and reference gap ![]() for a superimposed control voltage
for a superimposed control voltage ![]() yielding
yielding
![]()
The second term on the right hand side describes the behaviour of a spring element with
negative stiffness, and this must be softer than the mechanical springs: those linking PGB
to the spacecraft body and those connecting each test masses to the central rod. The
actuator is driven by a power amplifier modulated by the controller output signal. It
provides the control voltage ![]() to the capacitive load constituted by the pair of electrostatic actuators.
The resulting transfer function between the controller output signal
to the capacitive load constituted by the pair of electrostatic actuators.
The resulting transfer function between the controller output signal ![]() and the control voltage
and the control voltage ![]() is (the variable s
indicates a Laplace transform with respect to time)
is (the variable s
indicates a Laplace transform with respect to time)
![]()
with ![]() the stationary
gain and
the stationary
gain and ![]() the power
amplifier bandwidth. The transfer function between the displacement from the reference
position of the rotor and the sensor output signal
the power
amplifier bandwidth. The transfer function between the displacement from the reference
position of the rotor and the sensor output signal ![]() , including the conditioning circuitry, is
, including the conditioning circuitry, is
![]()
with ![]() the stationary
gain and
the stationary
gain and ![]() the sensor
bandwidth. In order to behave as required by Eq. 16 the controller
must supply the output signals
the sensor
bandwidth. In order to behave as required by Eq. 16 the controller
must supply the output signals ![]() and
and ![]() for the plates acting respectively in
for the plates acting respectively in ![]() and
and ![]() directions in accordance with the sensor outputs
directions in accordance with the sensor outputs ![]() and
and ![]() in the same directions. The
input-output relationships of the controller can be written in the form
in the same directions. The
input-output relationships of the controller can be written in the form
![]()
with ![]() and
and ![]() the stationary gains,
and
the stationary gains,
and ![]() the time
constant of the causal pole of the derivative term. By comparing Eq. 16 ,
Eq. 21 it follows that the stationary gains of the controller must
satisfy the relationships
the time
constant of the causal pole of the derivative term. By comparing Eq. 16 ,
Eq. 21 it follows that the stationary gains of the controller must
satisfy the relationships
![]()
It is easy to verify that a gain ![]() can be obtained with
can be obtained with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . The negative stiffness of
the electrostatic damper due to
. The negative stiffness of
the electrostatic damper due to ![]() is
is ![]() ,
lower than the stiffness of the springs.
,
lower than the stiffness of the springs.
We have shown the feasibility of an electrostatic active damper with the characteristics required to ensure stability. The approximations introduced, particularly as far as the simulation of the electric circuit is concerned, are quite rough. Also, the dynamics of the sensors, controllers and power amplifiers has been neglected. However, the results are essentially correct because the frequencies at which the system works are quite low, orders of magnitude smaller than the characteristic frequencies of the electronic subsystems.
As for the thermal noise of the electrostatic active damper we have:
![]()
where ![]() is the
equivalent resistance of the electrostatic damper of capacity
is the
equivalent resistance of the electrostatic damper of capacity ![]() and electric quality
factor
and electric quality
factor ![]() operated at
frequency
operated at
frequency ![]() . Then,
. Then,
![]()
Since the force exerted by the damper is ![]() (
(![]() the potential difference) the perturbing force corresponding to the noise is
the potential difference) the perturbing force corresponding to the noise is ![]()
![]() . Dividing by the mass
. Dividing by the mass ![]() of the test body we get the
perturbing acceleration:
of the test body we get the
perturbing acceleration:
![]()
A comparison with the mechanical thermal noise (Section
6.2 ) shows that with a reasonable value of the electric quality factor ![]() , and
, and ![]() the contribution of each
electrostatic damper to the thermal noise is negligible and it remains so even considering
that the damping of each test body involves 8 capacitance plates. This result could be
guessed from the fact that the force to be provided by each plate is very small. In point
of fact we plan to confirm this result with experimental tests of the electrostatic
damping system in the framework of a ground experimental test of the equivalence principle
based, as GG, on supercritical rotation and mechanical suspension of concentric test
cylinders.
the contribution of each
electrostatic damper to the thermal noise is negligible and it remains so even considering
that the damping of each test body involves 8 capacitance plates. This result could be
guessed from the fact that the force to be provided by each plate is very small. In point
of fact we plan to confirm this result with experimental tests of the electrostatic
damping system in the framework of a ground experimental test of the equivalence principle
based, as GG, on supercritical rotation and mechanical suspension of concentric test
cylinders.
Let us now estimate the amount of shot noise to be expected:
![]()
where ![]() and
and ![]() is the potential difference
due to the quantized current
is the potential difference
due to the quantized current ![]() . With a capacity
. With a capacity ![]() for
each electrostatic damper we get:
for
each electrostatic damper we get:
![]()
If ![]() (but usually is
much smaller) the shot noise is about 5 times bigger than the thermal noise given by Eq. 24 , which we have just seen to be negligible with respect to the
mechanical thermal noise of the test masses.
(but usually is
much smaller) the shot noise is about 5 times bigger than the thermal noise given by Eq. 24 , which we have just seen to be negligible with respect to the
mechanical thermal noise of the test masses.
We have seen in Section 3 that a position of relative
equilibrium exists, naturally provided by the physics of the system, where the spin axes
of the test bodies are extremely close to one another (![]() in this case). It is worth recalling that the direction of this
miscentering is fixed in the rotating system, its location depending on the direction of
the original unbalance (by construction and mounting). We have also seen that slow (at the
natural frequencies) whirl motions around this relative equilibrium can be damped by
active electrostatic sensors/actuators rotating with the system. If the sensing errors
allow them to detect displacements as small as the miscentering, the tidal perturbation
(in the transverse plane), which is linear with the miscentering, is about 20 times
smaller than the EP violation signal we are trying to measure. In case of higher sensing
errors, the output signal can be analized to remove tidal variations at the natural
frequencies.
in this case). It is worth recalling that the direction of this
miscentering is fixed in the rotating system, its location depending on the direction of
the original unbalance (by construction and mounting). We have also seen that slow (at the
natural frequencies) whirl motions around this relative equilibrium can be damped by
active electrostatic sensors/actuators rotating with the system. If the sensing errors
allow them to detect displacements as small as the miscentering, the tidal perturbation
(in the transverse plane), which is linear with the miscentering, is about 20 times
smaller than the EP violation signal we are trying to measure. In case of higher sensing
errors, the output signal can be analized to remove tidal variations at the natural
frequencies.
The centres of mass of the test bodies could as well be a
distance ![]() away from one another
along the axis itself, thus also giving rise to a tidal force. Were the spin axis exactly
perpendicular to the orbit plane, the tidal force would have no component perpendicular to
it. This not being exactly the case, such a component will appear, causing a relative
displacement of the centres of mass with respect to one another. This tidal perturbation
is, as in the case of an EP violation, a differential force directed towards the centre of
the Earth slowly changing its direction as the satellite orbits the Earth. However, it can
be distinguished from an EP violation signal and indeed used to drive a servo mechanism
for reducing the vertical displacement
away from one another
along the axis itself, thus also giving rise to a tidal force. Were the spin axis exactly
perpendicular to the orbit plane, the tidal force would have no component perpendicular to
it. This not being exactly the case, such a component will appear, causing a relative
displacement of the centres of mass with respect to one another. This tidal perturbation
is, as in the case of an EP violation, a differential force directed towards the centre of
the Earth slowly changing its direction as the satellite orbits the Earth. However, it can
be distinguished from an EP violation signal and indeed used to drive a servo mechanism
for reducing the vertical displacement ![]() from its initial value of
from its initial value of ![]() obtained by construction down to below the sensitivity of the experiment.
This is possible for two reasons: i) Unlike EP violation, these tidal forces have opposite
directions on opposite sides of the Earth, depending on which mass is closer to the Earth
(Fig. 10 ). This means that the tidal signal differs from an EP
violation signal by the orbital frequency of the satellite, a difference which is
detectable by measuring the spin rate of the spacecraft. ii) While the tidal force goes to
zero with
obtained by construction down to below the sensitivity of the experiment.
This is possible for two reasons: i) Unlike EP violation, these tidal forces have opposite
directions on opposite sides of the Earth, depending on which mass is closer to the Earth
(Fig. 10 ). This means that the tidal signal differs from an EP
violation signal by the orbital frequency of the satellite, a difference which is
detectable by measuring the spin rate of the spacecraft. ii) While the tidal force goes to
zero with ![]() , the EP violation force
doesn't, i.e. mass centering does not change an EP violation signal.
, the EP violation force
doesn't, i.e. mass centering does not change an EP violation signal.
Fig. 10. Simple scheme of Earth tidal forces on two test bodies which rotate around the same axis but are displaced along it. The figure shows how the component of the tidal force towards the Earth changes phase by
every half orbital period of the satellite around the Earth. Only this component does produce a differential displacement of the centres of mass which can be recorded by the spinning capacitors. It is apparent that a differential force due to a violation of the equivalence principle would not change sign every
orbit and would not go to zero with the separation distance
.
If the spin axis is an angle ![]() away from the perpendicular to the orbit plane, and the bodies are at a
distance
away from the perpendicular to the orbit plane, and the bodies are at a
distance ![]() along the spin axis, the
tidal acceleration on each test mass has a component perpendicular to the spin axis:
along the spin axis, the
tidal acceleration on each test mass has a component perpendicular to the spin axis:
![]()
Allowing for an angle ![]() , this
gives
, this
gives ![]() in order to have a
perturbation to the level of the signal. With the capacitance read out system discussed in
Section 7 it is no problem at all to detect miscentering
down to the required value and use the piezoelectric actuators shown in Fig.
2 for active centering. Once the tidal acceleration signal has become too small to be
detected it will also be too small to perturb the EP experiment. Using the tidal signal
for axial centering of the test bodies was originally suggested for STEP (Worden et al., 1990). Besides the differential
effect of Earth tides on the test masses, one must also consider the common mode tidal
perturbation with respect to the centre of mass of the entire system. In particular, for
the test bodies located inside the two experimental chambers above and below the centre of
mass (Fig. 1 ), the distance
in order to have a
perturbation to the level of the signal. With the capacitance read out system discussed in
Section 7 it is no problem at all to detect miscentering
down to the required value and use the piezoelectric actuators shown in Fig.
2 for active centering. Once the tidal acceleration signal has become too small to be
detected it will also be too small to perturb the EP experiment. Using the tidal signal
for axial centering of the test bodies was originally suggested for STEP (Worden et al., 1990). Besides the differential
effect of Earth tides on the test masses, one must also consider the common mode tidal
perturbation with respect to the centre of mass of the entire system. In particular, for
the test bodies located inside the two experimental chambers above and below the centre of
mass (Fig. 1 ), the distance ![]() in Eq. 28 cannot be smaller than about
in Eq. 28 cannot be smaller than about ![]() , thus resulting in a common mode tidal
perturbation of about
, thus resulting in a common mode tidal
perturbation of about ![]() , also
differing from an EP violation signal by the orbital frequency of the spacecraft (Fig. 10 ). An adequate level of common mode rejection is therefore
necessary (see Section 5.2 ).
, also
differing from an EP violation signal by the orbital frequency of the spacecraft (Fig. 10 ). An adequate level of common mode rejection is therefore
necessary (see Section 5.2 ).
The effect of nongravitational forces - such as air drag and solar radiation pressure -
acting directly on the outer surface of the spacecraft and not on the suspended masses
inside, is twofold. On one side they shake the spacecraft and produce vibrational noise
whose spectral distribution covers a wide frequency range and depends on the particular
spacecraft. This is not a matter of concern for the GG experiment thanks to the PGB
mechanical suspension which is particularly effective at the ![]() frequency of the signal (Fig.
3 ). On the other side, nongravitational forces accelerate the satellite itself. Let
us consider air drag, which at
frequency of the signal (Fig.
3 ). On the other side, nongravitational forces accelerate the satellite itself. Let
us consider air drag, which at ![]() altitude dominates over solar radiation pressure (the effect of the Earth's albedo is even
smaller). The main component of air drag is in the along track direction of the satellite
with relatively large intensity variations and a slow change of direction over the orbital
period of the satellite around the Earth. If the spacecraft is not designed to counteract
air drag, it will loose altitude and accelerate in the along track direction, with the
result that the suspended bodies inside (the PGB laboratory as well as the test masses)
will be subject to inertial translational forces. The lifetime of the satellite because of
its orbit decay is
altitude dominates over solar radiation pressure (the effect of the Earth's albedo is even
smaller). The main component of air drag is in the along track direction of the satellite
with relatively large intensity variations and a slow change of direction over the orbital
period of the satellite around the Earth. If the spacecraft is not designed to counteract
air drag, it will loose altitude and accelerate in the along track direction, with the
result that the suspended bodies inside (the PGB laboratory as well as the test masses)
will be subject to inertial translational forces. The lifetime of the satellite because of
its orbit decay is ![]() ,
by far longer than a few hours integration time needed for the EP experiment (Section 6.2 ) and also much longer than a reasonable
mission duration which we foresee of several months to a year. The price we have to pay in
order to avoid the complexity and cost of a sophisticated drag free system is exactly in
the need to deal with these inertial translational forces. However, the first important
fact to learn is that, unlike the forces which act directly on the surface of the
spacecraft, inertial forces on the suspended bodies inside do not depend - in any way
- on the surface properties of these bodies. Whatever the non gravitational acceleration
on the satellite, the inertial force is simply given by the mass of the suspended body
times this acceleration, it is centred at the centre of mass of the body and directed
opposite to the nongravitational acceleration of the satellite. The balance between this
force and the restoring force of the suspending spring gives the new position of
equilibrium. Therefore, two suspended bodies with ideally equal masses and equal
suspensions would be subject to exactly the same inertial forces: were they originally
centred on one another with good enough precision for the EP experiment, they would
continue to be centred on one another with the same precision in spite of air resistance
acting on the spacecraft as well as of its variations.
,
by far longer than a few hours integration time needed for the EP experiment (Section 6.2 ) and also much longer than a reasonable
mission duration which we foresee of several months to a year. The price we have to pay in
order to avoid the complexity and cost of a sophisticated drag free system is exactly in
the need to deal with these inertial translational forces. However, the first important
fact to learn is that, unlike the forces which act directly on the surface of the
spacecraft, inertial forces on the suspended bodies inside do not depend - in any way
- on the surface properties of these bodies. Whatever the non gravitational acceleration
on the satellite, the inertial force is simply given by the mass of the suspended body
times this acceleration, it is centred at the centre of mass of the body and directed
opposite to the nongravitational acceleration of the satellite. The balance between this
force and the restoring force of the suspending spring gives the new position of
equilibrium. Therefore, two suspended bodies with ideally equal masses and equal
suspensions would be subject to exactly the same inertial forces: were they originally
centred on one another with good enough precision for the EP experiment, they would
continue to be centred on one another with the same precision in spite of air resistance
acting on the spacecraft as well as of its variations.
This amounts to saying that the effect of the translational inertial
forces on the suspended coaxial cylinders of the GG experiment is intrinsically
common mode. Any difference that may arise, due to either a difference in the masses
or a difference in the suspensions, will give a signal at the spinning frequency,
i.e. the same frequency as the signal. However, they differ in phase as well as in the
important property that while inertial differential forces go to zero with the relative
differences in m and k (i.e. they can in principle be made zero by
reducing ![]() and
and ![]() for the two bodies) the
differential force due to an EP violation would still be there no matter how equal
the masses of the test bodies and their suspensions are. The crucial question is
therefore: How much do we need the inertial forces on the suspended test bodies to equal
each other in order to be able to detect an EP differential acceleration
for the two bodies) the
differential force due to an EP violation would still be there no matter how equal
the masses of the test bodies and their suspensions are. The crucial question is
therefore: How much do we need the inertial forces on the suspended test bodies to equal
each other in order to be able to detect an EP differential acceleration ![]() (i.e.
(i.e. ![]() )? Making the signals equal is
usually referred to as Common Mode Rejection (CMR). Given the goal in EP testing,
the required CMR factor does depend on the value of the inertial force in common mode,
hence on the intensity of the air drag acceleration on the spacecraft which we therefore
try to keep as low as possible by making it small and compact. We have
)? Making the signals equal is
usually referred to as Common Mode Rejection (CMR). Given the goal in EP testing,
the required CMR factor does depend on the value of the inertial force in common mode,
hence on the intensity of the air drag acceleration on the spacecraft which we therefore
try to keep as low as possible by making it small and compact. We have ![]() , the same as the
area-to-mass of LAGEOS, the passive spherical satellite devoted to geodynamical studies.
It is compatible with the 3-chamber setup of Fig. 1 and a total mass
of about
, the same as the
area-to-mass of LAGEOS, the passive spherical satellite devoted to geodynamical studies.
It is compatible with the 3-chamber setup of Fig. 1 and a total mass
of about ![]() . Once the
orbiting altitude has been chosen the air density depends on the solar index, which
changes with a period of
. Once the
orbiting altitude has been chosen the air density depends on the solar index, which
changes with a period of ![]() . We refer to data on atmospheric density provided by the GTDS (Cappellari et al., 1976), as function of the
solar index and satellite altitude (a minimum and a maximum value are given for each
altitude because of the nonspherical shape of the isodensity surfaces of the Earth
atmosphere). The GTDS tables are based on the original atmospheric model of Harris & Priester (1952); Harris & Priester (1962) which has been
modified to include the dependence on the solar index and the asphericity of the
atmospheric bulge. They are used by NASA and other space centres around the world for
mission analysis and have been shown to be in very good agreement with the more recent and
more sophisticated models (Jacchia, 1971; Roberts, 1971). If the mission is flown at
. We refer to data on atmospheric density provided by the GTDS (Cappellari et al., 1976), as function of the
solar index and satellite altitude (a minimum and a maximum value are given for each
altitude because of the nonspherical shape of the isodensity surfaces of the Earth
atmosphere). The GTDS tables are based on the original atmospheric model of Harris & Priester (1952); Harris & Priester (1962) which has been
modified to include the dependence on the solar index and the asphericity of the
atmospheric bulge. They are used by NASA and other space centres around the world for
mission analysis and have been shown to be in very good agreement with the more recent and
more sophisticated models (Jacchia, 1971; Roberts, 1971). If the mission is flown at ![]() altitude and the solar index is
altitude and the solar index is ![]() (the solar index F in the GTDS tables
goes from a minimum of 65 to a maximum of 275), the average air density is
(the solar index F in the GTDS tables
goes from a minimum of 65 to a maximum of 275), the average air density is ![]() . The corresponding
acceleration on the spacecraft is:
. The corresponding
acceleration on the spacecraft is: ![]() , with
, with ![]() the orbital velocity of the spacecraft and
the orbital velocity of the spacecraft and ![]() its aerodynamic coefficient. The inertial common
mode acceleration on the test masses is therefore
its aerodynamic coefficient. The inertial common
mode acceleration on the test masses is therefore ![]() with direction opposite to the drag acceleration.
The equilibrium position discussed in Section 3 (where
the centrifugal force due to the spin is balanced by the restoring force of the mechanical
suspensions) will be displaced - in common mode - by an amount
with direction opposite to the drag acceleration.
The equilibrium position discussed in Section 3 (where
the centrifugal force due to the spin is balanced by the restoring force of the mechanical
suspensions) will be displaced - in common mode - by an amount ![]() , each body spinning around
its own axis displaced in the new position. Since the precise location of the laboratory,
as well as the test bodies (in common mode!) is not needed, this displacement of the
position of equilibrium - which is the main effect of the translational inertial forces -
is no problem at all.
, each body spinning around
its own axis displaced in the new position. Since the precise location of the laboratory,
as well as the test bodies (in common mode!) is not needed, this displacement of the
position of equilibrium - which is the main effect of the translational inertial forces -
is no problem at all.
Indeed, the perturbation due to the air drag can be further reduced by
flying the spacecraft at higher altitude: in going from ![]() to
to ![]() altitude the EP violation signal decreases only slightly while the drag effect is
significantly reduced due to a much smaller air density. For instance, at
altitude the EP violation signal decreases only slightly while the drag effect is
significantly reduced due to a much smaller air density. For instance, at ![]() altitude during a solar minimum (
altitude during a solar minimum (![]() in the GTDS tables) the maximum air density
is
in the GTDS tables) the maximum air density
is ![]() , resulting in
an acceleration on the spacecraft of
, resulting in
an acceleration on the spacecraft of ![]() , only slightly exceeding the perturbation due to the solar radiation
pressure:
, only slightly exceeding the perturbation due to the solar radiation
pressure: ![]() (with
(with ![]() the solar
constant and c the velocity of light). This effect has a phase difference as well
as a small relative difference in frequency with respect to an EP violation signal in the
field of the Earth, as discussed in Section 2.3 . The
effect of Earth's albedo is smaller than the solar radiation effect because of the albedo
coefficient of the Earth (
the solar
constant and c the velocity of light). This effect has a phase difference as well
as a small relative difference in frequency with respect to an EP violation signal in the
field of the Earth, as discussed in Section 2.3 . The
effect of Earth's albedo is smaller than the solar radiation effect because of the albedo
coefficient of the Earth (![]() ); it also has
an extremely clear signature because of its following the entering of the satellite in and
out of the Earth's shadow.
); it also has
an extremely clear signature because of its following the entering of the satellite in and
out of the Earth's shadow.
The accuracy that can be achieved in the detection of an EP violation differential
force relies crucially on the ability to reject the common mode effect of inertial forces
on the test masses, which in turn is limited by the ability to balance the test bodies.
This because it is much easier to make the masses equal than it is to equal the
suspensions. As we have seen, the largest perturbation to compete with an EP violation
signal is the inertial force resulting from air drag (![]() ), with the same frequency and
), with the same frequency and ![]() phase difference, while a
phase difference, while a ![]() confidence level in the expected signal
requires a sensitivity of
confidence level in the expected signal
requires a sensitivity of ![]() . If we
show that a total common mode rejection by
. If we
show that a total common mode rejection by ![]() can be achieved, so as to bring the differential effect of the inertial force
due to air drag down to
can be achieved, so as to bring the differential effect of the inertial force
due to air drag down to ![]() then, since a factor 2 for the separation of effects with about
then, since a factor 2 for the separation of effects with about ![]() phase difference is generally accepted among
experimentalists, we are below the required sensitivity (see Fig. 11 ).
phase difference is generally accepted among
experimentalists, we are below the required sensitivity (see Fig. 11 ).
Fig. 11. Qualitative representation, in the orbital plane and for one pair of test masses, of the differential displacements obtained from the synchronous demodulation of the 2-phase
signal. The x-axis is in the Earth-to-satellite direction and the vector
is the differential displacement, directed along the x-axis and constant in amplitude, of the two masses due to an EP violation. The perturbation
due to the initially unbalanced atmospheric drag will be found in the area between the two dotted lines crossing in P: the angle between them is about
, and is due to the fact that the drag has a variable component in the radial direction because of the solar radiation pressure (of amplitude about
times the atmospheric drag and in the Sun-satellite direction). Smaller contributions to the
vector come from the Earth albedo, the Earth infrared radiation and, by a smaller amount, from a possible small eccentricity of the orbit. By finely adjusting the lengths of the suspension arms the point D is displaced up or down inside this area, and this balancing of the drag should be continued until D is as close as possible to P. In doing so, also the radial component is automatically balanced. The resonant variations of the drag (not shown) will oscillate inside the same area. The vector
is the instability due to the internal dissipation of the springs (Section 3.2 ), slowly rotating and increasing: it must be actively damped until Q is as close as possible to D (and P). The circle around point Q represents the error in the measurement due to the thermal noise of the mechanical oscillations in a few days of integration time. The actual values of all these quantities are discussed in the text.
As for the masses, ![]() cylinders can certainly be made of equal mass to better than 1
part in
cylinders can certainly be made of equal mass to better than 1
part in ![]() . Making suspensions
springs that are equal to 1 part in
. Making suspensions
springs that are equal to 1 part in ![]() and stay equal for the required integration time (see Section 6.2 ) and hopefully longer, is more difficult.
First of all, we must distinguish between springs being equal and springs being stable.
The problem of stable (helicoidal) springs has been widely investigated and techniques
have been developed to reduce the release of accumulated stress. These include annealing
as well as carving from a single piece of material. An important area of application for
stable springs is in the construction of high sensitive gravimeters for accurate
measurement of Earth tides (Melchior, 1978). In
the 1-g environment, in absence of large shocks and temperature variations,
gravimeters with metallic springs have reached an absolute drift value of of 1 part
in
and stay equal for the required integration time (see Section 6.2 ) and hopefully longer, is more difficult.
First of all, we must distinguish between springs being equal and springs being stable.
The problem of stable (helicoidal) springs has been widely investigated and techniques
have been developed to reduce the release of accumulated stress. These include annealing
as well as carving from a single piece of material. An important area of application for
stable springs is in the construction of high sensitive gravimeters for accurate
measurement of Earth tides (Melchior, 1978). In
the 1-g environment, in absence of large shocks and temperature variations,
gravimeters with metallic springs have reached an absolute drift value of of 1 part
in ![]() per day and a thermal stability
of
per day and a thermal stability
of ![]() (Melchior et al., 1979). These figures come from
data recorded during a 1-yr (1978) measurement campaign at Alice Springs in Australia by
P. Melchior, B. Ducarme and collaborators using the Gravimčtre 4084 (Melchior et al., 1979). It has been pointed out
by Dr. Ducarme (Ducarme, 1994) that, although
these figures are instrument dependent, drifts of 1 part in
(Melchior et al., 1979). These figures come from
data recorded during a 1-yr (1978) measurement campaign at Alice Springs in Australia by
P. Melchior, B. Ducarme and collaborators using the Gravimčtre 4084 (Melchior et al., 1979). It has been pointed out
by Dr. Ducarme (Ducarme, 1994) that, although
these figures are instrument dependent, drifts of 1 part in ![]() per day are common in this field. This is
encouraging, especially taking into account that gravimeters' springs on Earth are subject
to deformations comparable to their length (along the direction of local gravity), while
inside the GG spacecraft the largest acceleration is only
per day are common in this field. This is
encouraging, especially taking into account that gravimeters' springs on Earth are subject
to deformations comparable to their length (along the direction of local gravity), while
inside the GG spacecraft the largest acceleration is only ![]() and the springs are deformed by less than
and the springs are deformed by less than ![]() . With an absolute drift of
. With an absolute drift of ![]() per day, it would take 100 days before
springs originally equal were to differ by 1 part in
per day, it would take 100 days before
springs originally equal were to differ by 1 part in ![]() .
.
It is apparent that the capability to reject the common mode effect of
inertial forces on the test masses is crucial for the EP experiment. Let us therefore
consider the problem of manufacturing equal suspension springs for the test masses inside
each chamber. A level ![]() can be achieved by construction on Earth with computer controlled precision
techniques. Once the springs have been properly built (carved, annealed, etc.) the problem
arises to check their properties, in order to establish to which extent they equal each
other, and to measure the level of flicker noise. It is apparent that hair-like springs
such as these cannot be loaded on Earth with the masses they are supposed to suspend in
space, and a scaled model would not be of great value. It has been suggested by V.B.
Braginsky (Braginsky, 1993) to use appropriate
torsion balances such that motion in the horizontal plane is dominated by the elastic
constant of the springs; by mounting the springs as in Fig. 12 , and
using optical measurement techniques it is possible to measure how equal are the elastic
constants, the amount of their variation with time and the level of flicker noise.
can be achieved by construction on Earth with computer controlled precision
techniques. Once the springs have been properly built (carved, annealed, etc.) the problem
arises to check their properties, in order to establish to which extent they equal each
other, and to measure the level of flicker noise. It is apparent that hair-like springs
such as these cannot be loaded on Earth with the masses they are supposed to suspend in
space, and a scaled model would not be of great value. It has been suggested by V.B.
Braginsky (Braginsky, 1993) to use appropriate
torsion balances such that motion in the horizontal plane is dominated by the elastic
constant of the springs; by mounting the springs as in Fig. 12 , and
using optical measurement techniques it is possible to measure how equal are the elastic
constants, the amount of their variation with time and the level of flicker noise.
Fig. 12. Testing of suspension springs. By means of a torsion pendulum one can make ground tests of the longitudinal (a) and of the transversal (b) characteristics of the very thin and weak springs that will be used in orbit at zero g. One can test one spring at a time or, as shown in this figure, measure the differences between two of them.
We therefore assume a common mode rejection, by construction, of ![]() and plan to achieve the required level
of
and plan to achieve the required level
of ![]() during a calibration phase at
the beginning of the mission in which any
during a calibration phase at
the beginning of the mission in which any ![]() signal detected by the read out system is reduced down to the expected
signal. In order to make this possible a coupled suspension of the test masses is proposed
(see Fig. 2 ). The masses are attached by means of soft springs to
the ends of two rods, and each rod is pivoted at its middle point on elastic gimbals so
that it can change orientation by small amounts in all directions. In this way the
frequency of oscillations in common mode depends on the elastic constant k of the
suspension springs, while the frequency of oscillations in differential mode (i.e. of one
mass with respect to the other) depends on
signal detected by the read out system is reduced down to the expected
signal. In order to make this possible a coupled suspension of the test masses is proposed
(see Fig. 2 ). The masses are attached by means of soft springs to
the ends of two rods, and each rod is pivoted at its middle point on elastic gimbals so
that it can change orientation by small amounts in all directions. In this way the
frequency of oscillations in common mode depends on the elastic constant k of the
suspension springs, while the frequency of oscillations in differential mode (i.e. of one
mass with respect to the other) depends on ![]() , where
, where ![]() is the elastic constant of the torsion wires of the gimbals and l is
the length of each of the four halves of the two rods connecting the gimbals to the
springs. Thus, by adjusting the length of the rods it is possible to balance the effect of
forces which are inherently common mode but nonetheless give a differential effect because
of small differences in the elastic constant of the suspensions. Were the masses suspended
independently (i.e. springs attached directly to PGB laboratory without gimbals) the only
way to balance the effect of perturbations in common mode would be by in flight changes of
the elastic constant of the springs itself, which would be very hard to achieve and
control.
is the elastic constant of the torsion wires of the gimbals and l is
the length of each of the four halves of the two rods connecting the gimbals to the
springs. Thus, by adjusting the length of the rods it is possible to balance the effect of
forces which are inherently common mode but nonetheless give a differential effect because
of small differences in the elastic constant of the suspensions. Were the masses suspended
independently (i.e. springs attached directly to PGB laboratory without gimbals) the only
way to balance the effect of perturbations in common mode would be by in flight changes of
the elastic constant of the springs itself, which would be very hard to achieve and
control.
Fig. 13. The system of piezoelectric actuators placed in the two balancing rods. The
and
signs represent the intrinsic polarization of the actuators, i.e. how each one of them must be oriented when mounted. Control voltages are applied to the actuators (when they are applied with the opposite polarity they should not exceed a certain value, which however is relatively high, so as not to risk to depolarize the piezoelectrics): the sum
determines the relative axial position of the barycentres of the test masses and is used for axial centering (Section 4 ). The voltage difference
can be used to change the lengths of the four halves of the rods so as to balance out the effect of transverse inertial forces (in particular the along-track component of the air drag).
Fig. 13 shows an enlargement of the elastic
gimbals and the piezoelectric actuators, with the polarization and the applied constant
voltages whose sum and difference allow us to adjust the axial position of the barycentres
(Section 4 ) and to displace the centres of mass of the
four halves of the two rods. In this way it is possible to compensate for any remaining
differences in the suspensions that would otherwise produce differential motions of the
test bodies under the effect of inertial and tidal forces, the driving signal for these
adjustments being the (demodulated) ![]() signal itself. To the achieved level of balance, no inertial force - no matter how
variable - will produce any relative displacement of the test masses. The system is
conceptually similar to an ordinary balance on the ground. Considering that sensitive
balances on the ground, at 1 g, can detect changes of weight of
signal itself. To the achieved level of balance, no inertial force - no matter how
variable - will produce any relative displacement of the test masses. The system is
conceptually similar to an ordinary balance on the ground. Considering that sensitive
balances on the ground, at 1 g, can detect changes of weight of ![]() -
-![]() (Quinn, 1993), and given the extremely
good properties of piezoceramics for fine adjustments, a similar common mode rejection
factor can be achieved with this system at almost zero g. Once no further reduction
is possible the phase and frequency of the signal must be analysed in order to establish
whether it is due to an EP violation. How can one be sure that an EP violation signal is
not eliminated together with the perturbing effects? This would only be possible for a
competing effect with the same frequency and phase as the signal in the case that it were
also constant in time. If the effects of drag and EP violation were parallel to each other
one could, for one particular value of the drag, balance the sum of the two; but drag is
variable, and therefore balancing would not hold. Furthermore, the two effects are in fact
about
(Quinn, 1993), and given the extremely
good properties of piezoceramics for fine adjustments, a similar common mode rejection
factor can be achieved with this system at almost zero g. Once no further reduction
is possible the phase and frequency of the signal must be analysed in order to establish
whether it is due to an EP violation. How can one be sure that an EP violation signal is
not eliminated together with the perturbing effects? This would only be possible for a
competing effect with the same frequency and phase as the signal in the case that it were
also constant in time. If the effects of drag and EP violation were parallel to each other
one could, for one particular value of the drag, balance the sum of the two; but drag is
variable, and therefore balancing would not hold. Furthermore, the two effects are in fact
about ![]() apart. Once the largest
common mode effect has been balanced it means that - to this level - the suspensions
respond the same, therefore also balancing all other common mode effects. Later checks of
the observed (if any)
apart. Once the largest
common mode effect has been balanced it means that - to this level - the suspensions
respond the same, therefore also balancing all other common mode effects. Later checks of
the observed (if any) ![]() signal
should be performed to make sure that there has been no long term variation of the
suspensions which may require to repeat the initial adjustment procedure.
signal
should be performed to make sure that there has been no long term variation of the
suspensions which may require to repeat the initial adjustment procedure.
Other experiments which require a good rejection of common mode
effects are worth considering in order to compare the different levels of CMR. Let us
first consider STEP, which is the closest experiment to GG and plans to reach a CMR factor
of ![]() (Worden et al., 1990; Barlier et al., 1991; Blaser et al., 1993; Blaser et al., 1994; Blaser et al., 1996). There is a major difference
between STEP and GG. The STEP configuration is unfavourable because a displacement signal
about 10 orders of magnitude smaller than the length of the symmetry axes of the test
masses is expected to take place just along the common direction of these axes, which
obviously means that any transversal perturbation in common mode can generate the same
type of signal if the two axes are not sufficiently well aligned. The CMR goal of STEP is
limited precisely by the capability to align the axes of the two accelerometers on one
another. This is not so in GG, where the signal acts in the plane perpendicular to the
spin/symmetry axes of the cylinders and common mode forces can be rejected very
effectively like in sensitive balances on the ground. Instead, STEP relies on drag-free
technology to partially compensate for the drag, which necessarily means relying on the
technology of mechanically tuned Helium thrusters. More advanced thrusters under
development in Europe have been proposed for STEP (Blaser
et al., 1994), namely FEEP, which have the advantages of very high specific impulse,
very fine electrical (rather than mechanical) tuning and negligible mass of propellant
(liquid Cs). However, since a large quantity of He propellant must be carried on board of
STEP anyway (in order to make the experiment cryogenic) and the boiled off He must in any
case be eliminated in a carefully controlled manner in order not to disturb the
experiment, it seems reasonable to use the boiled off He as propellant for the drag
compensation system, as originally proposed by Worden and Everitt. The use of FEEP
proposed by Blaser et al. (1994) for STEP was
instrumental to the competition within ESA and was soon proved not viable (Blaser et al., 1996).
(Worden et al., 1990; Barlier et al., 1991; Blaser et al., 1993; Blaser et al., 1994; Blaser et al., 1996). There is a major difference
between STEP and GG. The STEP configuration is unfavourable because a displacement signal
about 10 orders of magnitude smaller than the length of the symmetry axes of the test
masses is expected to take place just along the common direction of these axes, which
obviously means that any transversal perturbation in common mode can generate the same
type of signal if the two axes are not sufficiently well aligned. The CMR goal of STEP is
limited precisely by the capability to align the axes of the two accelerometers on one
another. This is not so in GG, where the signal acts in the plane perpendicular to the
spin/symmetry axes of the cylinders and common mode forces can be rejected very
effectively like in sensitive balances on the ground. Instead, STEP relies on drag-free
technology to partially compensate for the drag, which necessarily means relying on the
technology of mechanically tuned Helium thrusters. More advanced thrusters under
development in Europe have been proposed for STEP (Blaser
et al., 1994), namely FEEP, which have the advantages of very high specific impulse,
very fine electrical (rather than mechanical) tuning and negligible mass of propellant
(liquid Cs). However, since a large quantity of He propellant must be carried on board of
STEP anyway (in order to make the experiment cryogenic) and the boiled off He must in any
case be eliminated in a carefully controlled manner in order not to disturb the
experiment, it seems reasonable to use the boiled off He as propellant for the drag
compensation system, as originally proposed by Worden and Everitt. The use of FEEP
proposed by Blaser et al. (1994) for STEP was
instrumental to the competition within ESA and was soon proved not viable (Blaser et al., 1996).
Gravity gradiometers, which have reached a CMR level of ![]() (Park,
1990), may appear as possessing similarities with GG. As a matter of fact this is not
the case because they use separate and uncoupled accelerometers. To the contrary, in GG
the test masses are not separate but mechanically coupled: even though they are concentric
and very accurately aligned, the dynamics of their motion is similar to that of balances
and torsion balances (see Fig. 12 b where the wire is used only for
suspending and as an axis of rotation, without torsion) because they are suspended on the
opposite ends of two arms pivoted at their centres, as in balances and torsion balances.
The capability to reject common mode effects depends, in GG, on two facts: (a) the
stability of springs (both in time and with temperature); (b) the characteristics of the
piezoelectric actuators to be used for in flight adjustments of the length of the arms.
None of these crucial issues is of any concern for researchers on gravity gradiometers or
on STEP; hence there is no reason why the CMR factor of the GG apparatus should have any
relation to the CMR factor of these apparata. To the contrary, the issue of springs
stability is typically of great interest for scientists who build and use room temperature
gravimeters for accurate measurements of Earth tides, since spring gravimeters use similar
(metallic) springs and face very similar stability problems.
(Park,
1990), may appear as possessing similarities with GG. As a matter of fact this is not
the case because they use separate and uncoupled accelerometers. To the contrary, in GG
the test masses are not separate but mechanically coupled: even though they are concentric
and very accurately aligned, the dynamics of their motion is similar to that of balances
and torsion balances (see Fig. 12 b where the wire is used only for
suspending and as an axis of rotation, without torsion) because they are suspended on the
opposite ends of two arms pivoted at their centres, as in balances and torsion balances.
The capability to reject common mode effects depends, in GG, on two facts: (a) the
stability of springs (both in time and with temperature); (b) the characteristics of the
piezoelectric actuators to be used for in flight adjustments of the length of the arms.
None of these crucial issues is of any concern for researchers on gravity gradiometers or
on STEP; hence there is no reason why the CMR factor of the GG apparatus should have any
relation to the CMR factor of these apparata. To the contrary, the issue of springs
stability is typically of great interest for scientists who build and use room temperature
gravimeters for accurate measurements of Earth tides, since spring gravimeters use similar
(metallic) springs and face very similar stability problems.
Although the largest effect of air drag is at the orbital frequency of the satellite,
other low frequency variations (in the range from the orbital frequency to near the
threshold frequency of the PGB laboratory) which are too low to be damped by the
mechanical suspension, cannot be ruled out. They act on the test bodies as inertial forces
of which only the differential effect does matter as far as detecting an EP violation is
concerned; if a total CMR factor of ![]() is achieved, their common mode effect is also reduced by this factor. Furthermore, while
the inertial force resulting from the main along-track component of the drag is seen by
the capacitance sensors at exactly the same frequency as an EP violation signal (the
direction of the acceleration due to air drag changes at the orbital frequency just like
the satellite-to-Earth direction of an EP violation), a higher frequency variation of the
drag is seen by the sensors at a frequency differing from their spinning frequency with
respect to the centre of the Earth (i.e. the frequency of an EP violation) by an amount
which is given by the frequency of that particular air drag variation (Fig.
11 ). Therefore, besides being reduced by common mode rejection these effects can be
distinguished by measuring the rotation rate of the spacecraft with ordinary star trackers
or Earth elevation sensors. After the demodulation of the signal at
is achieved, their common mode effect is also reduced by this factor. Furthermore, while
the inertial force resulting from the main along-track component of the drag is seen by
the capacitance sensors at exactly the same frequency as an EP violation signal (the
direction of the acceleration due to air drag changes at the orbital frequency just like
the satellite-to-Earth direction of an EP violation), a higher frequency variation of the
drag is seen by the sensors at a frequency differing from their spinning frequency with
respect to the centre of the Earth (i.e. the frequency of an EP violation) by an amount
which is given by the frequency of that particular air drag variation (Fig.
11 ). Therefore, besides being reduced by common mode rejection these effects can be
distinguished by measuring the rotation rate of the spacecraft with ordinary star trackers
or Earth elevation sensors. After the demodulation of the signal at ![]() (Fig. 11 ) they appear
as very regular oscillations (due to the high Q; see Section 6.2 )) at about
(Fig. 11 ) they appear
as very regular oscillations (due to the high Q; see Section 6.2 )) at about ![]() with respect to a constant signal, and are therefore easily
distinguishable. By taking the average value of two measurements at a time interval of
half their period we can determine the centre of the oscillations with an error
with respect to a constant signal, and are therefore easily
distinguishable. By taking the average value of two measurements at a time interval of
half their period we can determine the centre of the oscillations with an error ![]() , which is certainly better
than we need.
, which is certainly better
than we need.
The GG coupled test bodies have low natural frequencies of oscillation
both in common mode and in differential mode (see Section
3.2 ). There will be air drag disturbances at these frequencies due to air density
variations ("air granularities") over distance scales of about a thousand
km. The corresponding density is smaller than average atmospheric density, typically by at
least a factor of 10. For these disturbances to resonate with the natural frequencies of
the system, they must act at a frequency whose distance from the resonant frequency ![]() is within the width of the
gaussian, namely
is within the width of the
gaussian, namely ![]() .
With
.
With ![]() for the test
bodies of the GG experiment (see Section 6.2 ) there
is no way that air granularities over a thousand km can act on the spacecraft so precisely
close to the natural frequencies of the test bodies.
for the test
bodies of the GG experiment (see Section 6.2 ) there
is no way that air granularities over a thousand km can act on the spacecraft so precisely
close to the natural frequencies of the test bodies.
We conclude this section on inertial forces by saying that this
version of GG is designed in such way that EP testing is possible without eliminating the
common mode effect of air drag. Its differential effect on the test masses is transformed
by the mechanical suspension in a difference of inertial forces that can therefore be
adequately reduced, partly by construction in the ground laboratory, partly by small and
fine in flight adjustments at the beginning of the mission. It might be necessary to
repeat the calibration, but only a few times during the ![]() duration of the mission. Such adjustments of differential effects
are much smaller and less demanding than it would be to counteract the effect of air drag
itself on the spacecraft. Indeed, beside being required only once (or a few times), they
are extremely fine for them to be realized with piezoceramics, whose precision and
reliability as actuators are well known, thus avoiding any thruster firing.
duration of the mission. Such adjustments of differential effects
are much smaller and less demanding than it would be to counteract the effect of air drag
itself on the spacecraft. Indeed, beside being required only once (or a few times), they
are extremely fine for them to be realized with piezoceramics, whose precision and
reliability as actuators are well known, thus avoiding any thruster firing.
It is well known that a small force gravitational experiment in space should avoid the presence of nearby moving masses. Therefore, were a refrigerating material carried on board the spacecraft - close to the apparatus - in order to lower the temperature, it should be accurately confined, which is neither easy nor inexpensive. We choose to operate the experiment at room temperature and find that, because of the (relatively) high spin rate of the spacecraft and the intrinsic differential nature of the signal, it is possible to obtain an adequate level of temperature stability by passive thermal isolation only (Section 6.1 ). As for thermal noise, we use bigger test masses than STEP in order to compensate for the fact of operating at higher temperature (Section 6.2 ). A capacitance read out system which exploits the differential nature of the experiment can provide an adequate measurement accuracy (Section 7 ) with no need to resort to a low temperature measurement device.
For the reasons discussed in Section 2.2 a ![]() altitude, almost equatorial, almost circular
orbit is the best choice for the experiment. However, on this orbit the satellite spends
almost half of its time in the shadow of the Earth and the rest in sunlight, thermal
equilibrium temperatures in the two cases differing by several tens of degree. While
azimuthal temperature variations are inexistent because of the the fast spin, temperature
gradients between the illuminated and the dark side of the satellite when exposed to
radiation can in principle be very large. These gradients can be essentially eliminated
inside a rapidly spinning spacecraft if it is properly insulated. Insulation and vacuum
serve also the purpose of reducing the rate of temperature variation with time.
Temperature stability in time inside the PGB laboratory should be of
altitude, almost equatorial, almost circular
orbit is the best choice for the experiment. However, on this orbit the satellite spends
almost half of its time in the shadow of the Earth and the rest in sunlight, thermal
equilibrium temperatures in the two cases differing by several tens of degree. While
azimuthal temperature variations are inexistent because of the the fast spin, temperature
gradients between the illuminated and the dark side of the satellite when exposed to
radiation can in principle be very large. These gradients can be essentially eliminated
inside a rapidly spinning spacecraft if it is properly insulated. Insulation and vacuum
serve also the purpose of reducing the rate of temperature variation with time.
Temperature stability in time inside the PGB laboratory should be of ![]() for the required integration time of about
2.6 hours (Section 6.2 ), but possibly longer.
for the required integration time of about
2.6 hours (Section 6.2 ), but possibly longer.
Vacuum is needed also not to reintroduce acoustical noise on the PGB
laboratory and the test masses. The vacuum level that can be achieved by means of a hole
to open space is that corresponding to atmospheric density. At ![]() altitude (where atmosphere is mostly
constituted by molecular oxygen)
altitude (where atmosphere is mostly
constituted by molecular oxygen) ![]() , hence
, hence ![]() . In fact the pressure may be about a factor
. In fact the pressure may be about a factor ![]() bigger because of outgassing. However, care should be taken in
avoiding materials with high levels of outgassing and in setting the size of the holes on
the basis of the outgassing area. Experience with resonant bar antennas for the detection
of gravitational waves shows that gold coated Kapton should be used instead of Mylar
because of its lower outgassing level. Any anisotropy in the internal outgassing (from
some particular spots) rotates with the test bodies and the sensors. It therefore gives an
essentially DC effect.
bigger because of outgassing. However, care should be taken in
avoiding materials with high levels of outgassing and in setting the size of the holes on
the basis of the outgassing area. Experience with resonant bar antennas for the detection
of gravitational waves shows that gold coated Kapton should be used instead of Mylar
because of its lower outgassing level. Any anisotropy in the internal outgassing (from
some particular spots) rotates with the test bodies and the sensors. It therefore gives an
essentially DC effect.
The heat sources that the satellite is exposed to are the Sun (![]() at the Earth's distance) and
the Earth itself, in the visible as well as in the infrared range. The Earth emits a
fraction of the sunlight given by its albedo (
at the Earth's distance) and
the Earth itself, in the visible as well as in the infrared range. The Earth emits a
fraction of the sunlight given by its albedo (![]() on average, although widely variable) i.e.
on average, although widely variable) i.e. ![]() . In the infrared, at the surface, we have
. In the infrared, at the surface, we have ![]() . A source of heat from a
given direction will produce a temperature gradient across the satellite between the side
facing the source and the one away from it, and eventually a gradient across the test
bodies and the suspended springs. A temperature gradient across the test bodies is a
source of radiation pressure, and since the satellite is spinning, the resulting signal is
modulated at the spinning frequency (as measured with respect to the source of heat). The
spinning frequency with respect to the Earth, namely the source of an EP driving signal,
is not the same as the one with respect to the Sun, and they can be distinguished from one
another. However, possible temperature gradients due to the infrared radiation from the
Earth would have exactly the same signature as the EP violation we are testing. We must
therefore make sure that internal temperature gradients be adequately small. Indeed, we
can see that temperature gradients across a rapidly spinning spacecraft can be reduced by
many orders of magnitude by means of an insulating outer shell and the vacuum inside.
. A source of heat from a
given direction will produce a temperature gradient across the satellite between the side
facing the source and the one away from it, and eventually a gradient across the test
bodies and the suspended springs. A temperature gradient across the test bodies is a
source of radiation pressure, and since the satellite is spinning, the resulting signal is
modulated at the spinning frequency (as measured with respect to the source of heat). The
spinning frequency with respect to the Earth, namely the source of an EP driving signal,
is not the same as the one with respect to the Sun, and they can be distinguished from one
another. However, possible temperature gradients due to the infrared radiation from the
Earth would have exactly the same signature as the EP violation we are testing. We must
therefore make sure that internal temperature gradients be adequately small. Indeed, we
can see that temperature gradients across a rapidly spinning spacecraft can be reduced by
many orders of magnitude by means of an insulating outer shell and the vacuum inside.
A cylindrical shell spinning with period P and exposed to the
solar flux ![]() (e.g.
perpendicular to the spin axis) will have a temperature gradient
(e.g.
perpendicular to the spin axis) will have a temperature gradient ![]() where
where ![]() is the density of the
shell,
is the density of the
shell, ![]() its
absorption coefficient (absorbed to impinging flux), w its thickness and
its
absorption coefficient (absorbed to impinging flux), w its thickness and ![]() its specific heat. For a spin
period
its specific heat. For a spin
period ![]() and
and ![]() the typical value of
the typical value of ![]() is around
is around ![]() degree for a good insulator (e.g. glass) and
degree for a good insulator (e.g. glass) and ![]() for a good heat conductor
(e.g. Copper). However, if the spin period of the shell is much smaller than the timescale
of its thermal inertia, it is as if it were subject to an isotropic flux, hence resulting
in a negligible gradient.
for a good heat conductor
(e.g. Copper). However, if the spin period of the shell is much smaller than the timescale
of its thermal inertia, it is as if it were subject to an isotropic flux, hence resulting
in a negligible gradient.
Let the inner surface of the spacecraft cylindrical body be covered with an insulating shell; the temperature behaviour across the shell will be given by:
![]()
where ![]() is the
satellite initial temperature (when injected into its orbit),
is the
satellite initial temperature (when injected into its orbit), ![]() is the temperature of
external environment and d is the penetration depth. Since the spacecraft spins
fast we can assume that
is the temperature of
external environment and d is the penetration depth. Since the spacecraft spins
fast we can assume that ![]() is the same all over its surface. We have:
is the same all over its surface. We have:

where ![]() ,
, ![]() and
and ![]() are the density, specific
heat and thermal conductivity of the insulating shell. Taking for these quantities typical
values for Kapton or Mylar (as given by DUPONT or found by Immergut, 1984) we get
are the density, specific
heat and thermal conductivity of the insulating shell. Taking for these quantities typical
values for Kapton or Mylar (as given by DUPONT or found by Immergut, 1984) we get ![]() . If the insulating shell has a thickness
of
. If the insulating shell has a thickness
of ![]() , it is apparent from Eq. 29 that gradients of temperature in the plane perpendicular to the
symmetry axis are negligible. As for the top and bottom sides of the cylindrical
spacecraft, they can be coated with reflecting material (mirrors) in order to reduce solar
heating, since it would be differential. This technique is widely used, e.g., in
geosynchronous satellites. In addition, it is worth recalling a very important peculiarity
of the GG experiment, namely that the spacecraft is connected to the experimental
laboratory only through the hair-like suspension springs of the PGB laboratory (inside
which the requirement on thermal stability must be achieved) and that there is vacuum
inside the spacecraft. Hence, heat is transferred essentially by radiation (see below).
Temperature gradients along the symmetry axis modulated at the orbital frequency would
give an effect at the spin/signal frequency. Let us consider the effect of axial gradients
on the arms. A differential expansion of the arms in the coupled suspension of the test
masses would destroy the balancing and therefore reduce the capability to maintain the
required CMR factor of
, it is apparent from Eq. 29 that gradients of temperature in the plane perpendicular to the
symmetry axis are negligible. As for the top and bottom sides of the cylindrical
spacecraft, they can be coated with reflecting material (mirrors) in order to reduce solar
heating, since it would be differential. This technique is widely used, e.g., in
geosynchronous satellites. In addition, it is worth recalling a very important peculiarity
of the GG experiment, namely that the spacecraft is connected to the experimental
laboratory only through the hair-like suspension springs of the PGB laboratory (inside
which the requirement on thermal stability must be achieved) and that there is vacuum
inside the spacecraft. Hence, heat is transferred essentially by radiation (see below).
Temperature gradients along the symmetry axis modulated at the orbital frequency would
give an effect at the spin/signal frequency. Let us consider the effect of axial gradients
on the arms. A differential expansion of the arms in the coupled suspension of the test
masses would destroy the balancing and therefore reduce the capability to maintain the
required CMR factor of ![]() discussed
in Section 5.2 . We therefore need:
discussed
in Section 5.2 . We therefore need:
![]()
If ![]() is the expansion coefficient of
the arms and z the axial coordinate:
is the expansion coefficient of
the arms and z the axial coordinate:
![]()
Since materials with ![]() are common
and can be used for manufacturing the arms, it follows that axial temperature gradients
over the arm's length (a few cm) must be smaller than
are common
and can be used for manufacturing the arms, it follows that axial temperature gradients
over the arm's length (a few cm) must be smaller than ![]() , which is not a stringent requirement. Were it needed, one could
make the arms of a material with
, which is not a stringent requirement. Were it needed, one could
make the arms of a material with ![]() ,
thus allowing for gradients of
,
thus allowing for gradients of ![]() .
.
The average temperature of the spacecraft changes because of it going
in and out of the Earth shadow, i.e. the relevant frequency is the orbital one. In order
to keep the temperature stable with time we must reduce the incoming heat. Since the
cylindrical surface of the spacecraft must be covered with solar cells (in order to
generate the necessary electric power) the external surface will absorb most of the heat
and reach, more or less, equilibrium with the solar radiation. Hence, we need - on the
internal side of the spacecraft - an insulating shell in order to reduce the amount of
heat that will reach the interior of the satellite. The timescale ![]() of thermal inertia provided by an insulating
shell of thickness w is:
of thermal inertia provided by an insulating
shell of thickness w is:
![]()
with ![]() ,
, ![]() and
and ![]() the density, specific heat
and thermal conductivity of the insulating material. Then, the time variation of the
temperature at the internal surface of the insulating shell is:
the density, specific heat
and thermal conductivity of the insulating material. Then, the time variation of the
temperature at the internal surface of the insulating shell is:
![]()
(![]() and
and ![]() as defined above). Let us
consider one half satellite orbit in sunlight. At the end of half period in sunlight the
temperature of the internal surface of the insulating shell will be:
as defined above). Let us
consider one half satellite orbit in sunlight. At the end of half period in sunlight the
temperature of the internal surface of the insulating shell will be:
![]()
where ![]() is the
equilibrium temperature in sunlight. Using
is the
equilibrium temperature in sunlight. Using ![]() and the properties of materials like Kapton and Mylar we have
and the properties of materials like Kapton and Mylar we have ![]() , while
, while ![]() . The corresponding temperature variation (after
half period in sunlight) is:
. The corresponding temperature variation (after
half period in sunlight) is:
![]()
Similarly, the temperature variation after half period in the shadow of the Earth
(darkness) is:
![]()
where ![]() is the
equilibrium temperature of the satellite when in the dark. Let us consider a large
difference of
is the
equilibrium temperature of the satellite when in the dark. Let us consider a large
difference of ![]() between equilibrium
temperatures in sunlight and in darkness (when the satellite is exposed only to the
infrared radiation form the Earth), and a satellite initial temperature halfway between
the two. Then, the temperature variation on the internal side of the insulating shell
after half orbit period will be (in absolute value)
between equilibrium
temperatures in sunlight and in darkness (when the satellite is exposed only to the
infrared radiation form the Earth), and a satellite initial temperature halfway between
the two. Then, the temperature variation on the internal side of the insulating shell
after half orbit period will be (in absolute value) ![]() Obviously the two temperature variations (increase
when in sunlight and decrease when in darkness) will not cancel out. Let us take half of
each. This means that, after one full orbital period of the satellite around the Earth the
temperature on the internal side of the insulating shell is changed by:
Obviously the two temperature variations (increase
when in sunlight and decrease when in darkness) will not cancel out. Let us take half of
each. This means that, after one full orbital period of the satellite around the Earth the
temperature on the internal side of the insulating shell is changed by:
![]()
This is too much for our requirements. We now exploit the important fact of having good
vacuum inside the spacecraft, because it ensures that there is only radiative transfer of
heat (apart for the thin hair-like suspension springs of the PGB laboratory). Indeed, the
mean free path of gas molecules at room temperature and ![]() is about
is about ![]() ,
while we have about
,
while we have about ![]() (having
allowed a factor
(having
allowed a factor ![]() for outgassing).
We can also coat the external surface of the PGB with Kapton. Then, the amount of energy
transferred from the insulating shell to the Kapton coated external surface of the PGB
after 1 orbital period is:
for outgassing).
We can also coat the external surface of the PGB with Kapton. Then, the amount of energy
transferred from the insulating shell to the Kapton coated external surface of the PGB
after 1 orbital period is:
![]()
where ![]() is the Stefan-Boltzmann
constant,
is the Stefan-Boltzmann
constant, ![]() is the
emissivity of kapton and A the area of the surface involved (
is the
emissivity of kapton and A the area of the surface involved (![]() ). The corresponding temperature variation
of the PGB laboratory (made of Copper) is:
). The corresponding temperature variation
of the PGB laboratory (made of Copper) is:
![]()
where ![]() is the
specific heat of Copper and
is the
specific heat of Copper and ![]() is the mass of the PGB laboratory. We get
is the mass of the PGB laboratory. We get ![]() . After 5 days, i.e. about 76 orbits of the
satellite we shall have:
. After 5 days, i.e. about 76 orbits of the
satellite we shall have:
![]()
Multilayers of insulating material are usually used in cryogenic experiments (Haselden, 1971), because, if properly separated in
order to reduce heat conduction, they are known to provide a reduction of the transferred
power proportional to the number of layers employed. For instance, this technique is
successfully used to reduce the amount of input power on the very large cryostats which
enclose resonant bars (![]() ) for low
temperature detection of gravitational waves (the EXPLORER antenna at CERN, in Geneva, and
the NAUTILUS antenna in Frascati, Rome). Our problem is easier because of both the smaller
size of the device and the very tiny connection between the spacecraft and PGB. In any
case, from Eq. 41 it follows that a number of about 30 Kapton layers
(such as those commercially available from DUPONT, of
) for low
temperature detection of gravitational waves (the EXPLORER antenna at CERN, in Geneva, and
the NAUTILUS antenna in Frascati, Rome). Our problem is easier because of both the smaller
size of the device and the very tiny connection between the spacecraft and PGB. In any
case, from Eq. 41 it follows that a number of about 30 Kapton layers
(such as those commercially available from DUPONT, of ![]() thickness each) can provide the required level of
thermal stability.
thickness each) can provide the required level of
thermal stability.
As far as internal power sources are concerned, we recall that they will be rotating together with the entire system, so all resulting effects will be DC. We shall also take care to use low dissipation components. In addition, only the preamplifiers will be positioned on the supporting rod inside the hollow cylinder test bodies; all the remaining power sources will be placed on the internal surface of the spacecraft shell. The required number of wires can be accommodated either as independent helicoidal springs or by grouping them on a plastic support without any serious problem of degrading the reduction of vibrational noise since a low Q is required for the PGB suspensions. Most of the wires will go to the inch-worms, to the active dampers, to the locking-unlocking mechanisms and to the preamplifiers of the capacitance read out while only 4 wires go through the gimbals to the piezoceramics on the balancing arms (see Fig. 2 ). For the passage through the multilayer insulation on the outer side of the PGB laboratory we can use, if needed, a technique known as thermal sink, whereby the wire does not go straight inside but rather makes many turns so as to largely reduce the temperature gradient that it will bring in. This technique is currently employed in the EXPLORER and NAUTILUS cryogenic resonant bar antennas mentioned above.
LISA (Laser Interferometer Space Antenna) (Bender et al., 1994), a proposed space mission
for the detection of gravity waves, is another example of a noncryogenic space experiment
where a very good thermal stability is needed, to be achieved passively. For LISA the
requirement is of ![]() around
around ![]() . LISA has the advantage,
over GG, to be subject to a much smaller variation of the solar flux due to its
heliocentric orbit. However, GG has the advantage, over LISA, of spinning fast (while LISA
is space stabilized). In the ground torsion balance Eöt-Wash experiment (Su et al., 1994) (also noncryogenic) they use two
active temperature stabilization systems based on several temperature sensors in order to
achieve a stability of
. LISA has the advantage,
over GG, to be subject to a much smaller variation of the solar flux due to its
heliocentric orbit. However, GG has the advantage, over LISA, of spinning fast (while LISA
is space stabilized). In the ground torsion balance Eöt-Wash experiment (Su et al., 1994) (also noncryogenic) they use two
active temperature stabilization systems based on several temperature sensors in order to
achieve a stability of ![]() across the
experimental chamber. We recall that their balance rotates very slowly, with a period
of
across the
experimental chamber. We recall that their balance rotates very slowly, with a period
of ![]() , while the spin period of GG is
only
, while the spin period of GG is
only ![]() .
.
Residual gas particles inside the spacecraft accelerated by a
temperature gradient between two sides of a test body would result in an acceleration
necessarily different for the two bodies: ![]() with
with ![]() the density of the test mass. This is the radiometer effect that the STEP
experiment is concerned about. The reason why this is so is that in STEP the signal is
along the symmetry axis of the test cylinders; for a given residual gas pressure any
temperature gradient between the two bases of each cylinder will result in an acceleration
along its symmetry axis, and it would inevitably be a differential acceleration; if
temperature variations are modulated at orbital frequency this would mimic an EP
violation. In STEP this problem is solved by having an extremely low residual gas pressure
(as low as
the density of the test mass. This is the radiometer effect that the STEP
experiment is concerned about. The reason why this is so is that in STEP the signal is
along the symmetry axis of the test cylinders; for a given residual gas pressure any
temperature gradient between the two bases of each cylinder will result in an acceleration
along its symmetry axis, and it would inevitably be a differential acceleration; if
temperature variations are modulated at orbital frequency this would mimic an EP
violation. In STEP this problem is solved by having an extremely low residual gas pressure
(as low as ![]() , made possible by very
low temperature) and a requirement for temperature gradients across each test body not to
exceed
, made possible by very
low temperature) and a requirement for temperature gradients across each test body not to
exceed ![]() . In the GG design this
effect is of no concern because the signal is normal to the symmetry axis of each
cylinder, hence if its inner and outer surface are at different temperatures, the net
force by thermally accelerated residual gas would be zero for symmetry reasons. Only if
temperature dos not have azimuthal symmetry there can be a radiometer effect; which is not
the case because of fast spin.
. In the GG design this
effect is of no concern because the signal is normal to the symmetry axis of each
cylinder, hence if its inner and outer surface are at different temperatures, the net
force by thermally accelerated residual gas would be zero for symmetry reasons. Only if
temperature dos not have azimuthal symmetry there can be a radiometer effect; which is not
the case because of fast spin.
The effect of viscous drag due to the residual gas on the centre of mass of the sensing bodies is well below the signal even under conservative assumptions. The effect is estimated according to Milani et al. (1987), Ch. 6, taking into account that the thermal velocity of the gas molecules is much higher than the velocity of the test bodies.
We must not forget that solar cells will necessarily cover the outer
surface of the spinning spacecraft whose temperature gradient can be as large as ![]() of a degree. It is only after
an appropriate insulating shell that this gradient is significantly reduced. Therefore we
must expect that the outermost layer of the spacecraft (essentially the solar cells) will
be subject to nonuniform thermal expansion at the spinning frequency. However, since the
part of the spacecraft involved in this oscillation is only the external one (because
temperature gradients are negligible inside) the result is a forced term acting on the
suspension at frequency
of a degree. It is only after
an appropriate insulating shell that this gradient is significantly reduced. Therefore we
must expect that the outermost layer of the spacecraft (essentially the solar cells) will
be subject to nonuniform thermal expansion at the spinning frequency. However, since the
part of the spacecraft involved in this oscillation is only the external one (because
temperature gradients are negligible inside) the result is a forced term acting on the
suspension at frequency ![]() , which will
be reduced according to the transfer function of Fig. 3 , and the
effect can be neglected. We must also expect that the outermost layer of the spacecraft
will be subject to nonuniform thermal expansion at the orbit frequency, resulting in a
common mode oscillation of the test masses at that frequency similar to the effect
produced by the along track component of air drag. With a typical expansion
coefficient
, which will
be reduced according to the transfer function of Fig. 3 , and the
effect can be neglected. We must also expect that the outermost layer of the spacecraft
will be subject to nonuniform thermal expansion at the orbit frequency, resulting in a
common mode oscillation of the test masses at that frequency similar to the effect
produced by the along track component of air drag. With a typical expansion
coefficient ![]() and a temperature
gradient which, thanks to the rapid spin, is not larger than about
and a temperature
gradient which, thanks to the rapid spin, is not larger than about ![]() , the oscillation amplitude of
the outer shell will be of a few
, the oscillation amplitude of
the outer shell will be of a few ![]() .
A common mode rejection of
.
A common mode rejection of ![]() is
enough to make this effect smaller than the signal (Section
5.2 ). As for the corresponding gravitational effects, they are found to be
negligible. The expansion/contraction of the outer shell of the spacecraft (due to it
entering and exiting the shadow of the Earth), the resulting changes in moment of inertia
and spin rate, and how to compensate for them are discussed in GALILEO GALILEI (1996) (Ch. 2.1).
is
enough to make this effect smaller than the signal (Section
5.2 ). As for the corresponding gravitational effects, they are found to be
negligible. The expansion/contraction of the outer shell of the spacecraft (due to it
entering and exiting the shadow of the Earth), the resulting changes in moment of inertia
and spin rate, and how to compensate for them are discussed in GALILEO GALILEI (1996) (Ch. 2.1).
We now investigate the effects of thermal expansion of the test
bodies. Let us first consider the simpler case in which the test bodies expand uniformly.
They will have expansion coefficients of the order of ![]() , because their composition is selected on the basis of EP
violation considerations and obviously not with the purpose of minimizing their thermal
expansion. Furthermore, their expansion coefficients will not be the same, and indeed we
shall assume that they differ by its entire value, namely that there is a difference in
their expansions by
, because their composition is selected on the basis of EP
violation considerations and obviously not with the purpose of minimizing their thermal
expansion. Furthermore, their expansion coefficients will not be the same, and indeed we
shall assume that they differ by its entire value, namely that there is a difference in
their expansions by ![]() too. However,
as long as they expand uniformly, there is no relative displacement of their
centres of mass and therefore no differential effect on the read out capacitors.
too. However,
as long as they expand uniformly, there is no relative displacement of their
centres of mass and therefore no differential effect on the read out capacitors.
But test bodies will not be perfect, and in correspondence of
inhomogeneities in their mass distribution there might be a different response to
temperature variations. However, the direction of non uniform expansion being fixed with
the test body it is also fixed with respect to the sensors, which means that its effect is
DC and does not compete with an EP violation signal. Furthermore, it is also small because
of it being proportional to inhomogeneities of the test bodies. With a not too stringent
requirement on the mass density such as ![]() , and in the conservative assumption that mass inhomogeneities do
necessarily imply a nonuniform thermal expansion of the same level (i.e. with a
proportionality factor of 1), we get a relative motion of the centres of mass by
about
, and in the conservative assumption that mass inhomogeneities do
necessarily imply a nonuniform thermal expansion of the same level (i.e. with a
proportionality factor of 1), we get a relative motion of the centres of mass by
about ![]() , which means (for linear
dimensions of about
, which means (for linear
dimensions of about ![]() ) differential
displacements in the direction of the mass inhomogeneity by
) differential
displacements in the direction of the mass inhomogeneity by ![]() , which is perfectly satisfactory for a DC
signal.
, which is perfectly satisfactory for a DC
signal.
We must also consider the fact that a uniform (but different)
expansion of the test bodies will change the distances a and b of the
capacitors from the outer and inner surfaces - respectively - of the test bodies (Section 7 ). We shall see in Section
7 that in order to be sensitive to an EP violation of ![]() the read out capacitance plates must be centered
between the test masses to within
the read out capacitance plates must be centered
between the test masses to within ![]() Ĺ which, in relative terms means
Ĺ which, in relative terms means ![]() .
Active balancing to this level is done with inch-worm actuators (see Section 7 ) and can be repeated if necessary. A difference
in the expansion coefficients by
.
Active balancing to this level is done with inch-worm actuators (see Section 7 ) and can be repeated if necessary. A difference
in the expansion coefficients by ![]() and a thermal stability of
and a thermal stability of ![]() allow
us to maintain this level of balancing. However, were it necessary, there is a possibility
to reduce the differential displacement of the surfaces of the test bodies with respect to
the capacitance plates in between. We can build the frame which supports the capacitors
(see Fig. 2 ) using an appropriate alloy whose expansion coefficient
must be such to compensate for the differential expansion of the test bodies. Once the
material choice for the EP experiment has been made and the test bodies have been built
their radii and thermal expansion coefficients can be accurately measured, thus uniquely
determining the required value for the expansion coefficient of the frame. In this way it
is possible to reduce the differential expansion by about a factor of 10, thus reducing
the relative displacement.
allow
us to maintain this level of balancing. However, were it necessary, there is a possibility
to reduce the differential displacement of the surfaces of the test bodies with respect to
the capacitance plates in between. We can build the frame which supports the capacitors
(see Fig. 2 ) using an appropriate alloy whose expansion coefficient
must be such to compensate for the differential expansion of the test bodies. Once the
material choice for the EP experiment has been made and the test bodies have been built
their radii and thermal expansion coefficients can be accurately measured, thus uniquely
determining the required value for the expansion coefficient of the frame. In this way it
is possible to reduce the differential expansion by about a factor of 10, thus reducing
the relative displacement.
Finally, temperature variations will affect the stiffness of the
suspension springs and therefore change the value of the transversal elongation ![]() in response to the inertial force caused by
air drag acting on the spacecraft:
in response to the inertial force caused by
air drag acting on the spacecraft:
![]()
since ![]() is the required level of
CMR. With a maximum temperature change of
is the required level of
CMR. With a maximum temperature change of ![]() and
and ![]() as obtained in gravimeter springs (see Section 3.2 )
the effect is 10 times smaller than it is needed, thus allowing for a less good thermal
stability of the springs.
as obtained in gravimeter springs (see Section 3.2 )
the effect is 10 times smaller than it is needed, thus allowing for a less good thermal
stability of the springs.
All the above analysis of the perturbing effects to be expected in performing the experiment at room temperature is based on simple physical principles; a more detailed thermal analysis has been conducted in GALILEO GALILEI (1996) taking advantage of space industry experience on the subject.
Test masses will have their own mechanical thermal noise, resulting in a perturbing
thermal acceleration on the test mass ![]() that must be smaller than the signal acceleration
that must be smaller than the signal acceleration ![]() . At room temperature
. At room temperature ![]() we have:
we have:

where ![]() is the
Boltzmann constant,
is the
Boltzmann constant, ![]() is the mass of each test body,
is the mass of each test body, ![]() their natural frequency for differential oscillations, Q the
mechanical quality factor and
their natural frequency for differential oscillations, Q the
mechanical quality factor and ![]() the integration time.
the integration time.
If we take the ![]() value, as used in the numerical simulation of Section 3.2 , we get
value, as used in the numerical simulation of Section 3.2 , we get ![]() , which means that an integration time of
about
, which means that an integration time of
about ![]() is necessary
in order to reach a signal-to-noise ratio of 2. However, we have now manufactured
helicoidal springs similar to the ones to be used in the space experiment to suspend the
test masses GG (GALILEO GALILEI, 1996). By
setting the spring in horizontal oscillation (for the oscillations not to be affected by
local gravity) with vacuum, temperature and clamping similar to those expected in the
space experiment, and at the same frequency at which it will spin - hence undergo
deformations - in space, we could measure the mechanical quality factor getting a value
of
is necessary
in order to reach a signal-to-noise ratio of 2. However, we have now manufactured
helicoidal springs similar to the ones to be used in the space experiment to suspend the
test masses GG (GALILEO GALILEI, 1996). By
setting the spring in horizontal oscillation (for the oscillations not to be affected by
local gravity) with vacuum, temperature and clamping similar to those expected in the
space experiment, and at the same frequency at which it will spin - hence undergo
deformations - in space, we could measure the mechanical quality factor getting a value
of ![]() . Since losses due to the
electrostatic dampers are much smaller (Section 3.2 )
and all other parts are rigid with no expected dissipation, this result gives a realistic
value for the total mechanical losses (further improvement may be possible). Using
. Since losses due to the
electrostatic dampers are much smaller (Section 3.2 )
and all other parts are rigid with no expected dissipation, this result gives a realistic
value for the total mechanical losses (further improvement may be possible). Using ![]() in Eq. 45 we
get
in Eq. 45 we
get ![]() and an
integration time of about 2.6 hours for a signal-to-noise ratio of 2 as before.
and an
integration time of about 2.6 hours for a signal-to-noise ratio of 2 as before.
Note that in Eq. 44 , Eq. 45 we
have the natural frequency of oscillation of one test body with respect to the other
instead of the (higher) natural frequency of oscillations in common mode (![]() ). This is correct because,
since the two frequencies are not close (they differ by about a factor of 2) and Q
is high, the bandwidth of noise is so small that there is no significant contribution from
the thermal noise in common mode to the thermal noise in differential motion where the
effect of an EP violation would appear. It is also worth noticing that the perturbing
effect of thermal noise is proportional to
). This is correct because,
since the two frequencies are not close (they differ by about a factor of 2) and Q
is high, the bandwidth of noise is so small that there is no significant contribution from
the thermal noise in common mode to the thermal noise in differential motion where the
effect of an EP violation would appear. It is also worth noticing that the perturbing
effect of thermal noise is proportional to ![]() , which explains why - working at room temperature - it is
important to have test bodies of relatively large mass. In comparison with STEP we work at
100 times higher temperature and therefore use test bodies about 100 times more massive.
As for the thermal noise perturbation due to the PGB laboratory, i.e. the common mode
thermal noise of the platform, it is given by formulas similar to Eq. 44 ,
Eq. 45 with the natural frequency, mass and quality factor of the PGB
laboratory (higher mass, lower Q). Being a small common mode effect it is easily
rejected.
, which explains why - working at room temperature - it is
important to have test bodies of relatively large mass. In comparison with STEP we work at
100 times higher temperature and therefore use test bodies about 100 times more massive.
As for the thermal noise perturbation due to the PGB laboratory, i.e. the common mode
thermal noise of the platform, it is given by formulas similar to Eq. 44 ,
Eq. 45 with the natural frequency, mass and quality factor of the PGB
laboratory (higher mass, lower Q). Being a small common mode effect it is easily
rejected.
The displacements of the test masses are detected with a pair of capacitors in a circuit which is essentially an LC bridge, formed by two resonant coupled oscillators, as shown in Fig. 14 . The plates of the capacitors are sections of cylinders concentric to the test bodies (Fig. 15 ) and are supported by the frame shown in Fig. 2 .
Fig. 14. Outline of the read-out circuit. The two variable capacitors
and
and the two halves of the inductor L form an LC bridge whose output is proportional to the difference between the two capacitances.
Fig. 15. Each capacitor of the read-out system (see also Fig. 16 ) is formed by two surfaces, one for each of the two grounded masses, and one plate, to which a sinusoidal voltage is applied. Any differential displacement of the test masses with respect to the plates causes a loss of balance of the system and therefore an output signal.
Fig. 16. The surfaces of the capacitors before and after: a) a common mode displacement and b) a differential mode displacement.
A voltage signal ![]() of angular frequency
of angular frequency ![]() is applied to the bridge in order to shift the signal of interest to a frequency band with
a
is applied to the bridge in order to shift the signal of interest to a frequency band with
a ![]() noise as small as
possible. We consider
noise as small as
possible. We consider ![]() . The circuit has the greatest sensitivity when
. The circuit has the greatest sensitivity when ![]() and when also the output
circuit resonates at the same frequency
and when also the output
circuit resonates at the same frequency ![]() . Since
. Since ![]() we must have
we must have ![]() . Since the system has a bad heat dissipation, the amplitude of the signal
should not exceed, say, 1 Volt in order to reduce power dissipation. We set
. Since the system has a bad heat dissipation, the amplitude of the signal
should not exceed, say, 1 Volt in order to reduce power dissipation. We set ![]() with
with ![]() . The two capacitors of the
bridge
. The two capacitors of the
bridge ![]() and
and ![]() are shown in Fig. 15 . The signal is applied to the plates and the test masses are
electrically grounded. Let us call a and b the initial distances from the
plate to the inner and outer mass respectively, with
are shown in Fig. 15 . The signal is applied to the plates and the test masses are
electrically grounded. Let us call a and b the initial distances from the
plate to the inner and outer mass respectively, with ![]() . If a and b are small a simplified analysis can be
carried out assuming zero curvature parallel plates, and the initial values of the
capacity are then
. If a and b are small a simplified analysis can be
carried out assuming zero curvature parallel plates, and the initial values of the
capacity are then ![]() (where
(where ![]() is the
dielectric constant of vacuum). In the cylindrical geometry the algebra is somewhat more
complicated but with no relevant changes in the results. Any displacement of the test
masses will change
is the
dielectric constant of vacuum). In the cylindrical geometry the algebra is somewhat more
complicated but with no relevant changes in the results. Any displacement of the test
masses will change ![]() into
into ![]() for
for ![]() and
and ![]() for
for ![]() . Such a displacement is the
combination of a common mode and a differential mode displacement
. Such a displacement is the
combination of a common mode and a differential mode displacement ![]() ,
, ![]() (Fig. 16 ).
Because of
(Fig. 16 ).
Because of ![]() the
values of the capacity change into
the
values of the capacity change into
![]()
and therefore ![]() .
Similarly for
.
Similarly for ![]() we
have:
we
have:
![]()
hence, ![]() . For the
general displacement the total change of capacitance will be given by:
. For the
general displacement the total change of capacitance will be given by:
![]()
which at resonance determines the output signal through the relation:
![]()
where ![]() is the
electrical quality factor of the output circuit. For instance, if
is the
electrical quality factor of the output circuit. For instance, if ![]() ,
, ![]() ,
, ![]() and
and ![]() we get
we get ![]() and
and ![]() , given the
requirement to be sensitive to an EP displacement with
, given the
requirement to be sensitive to an EP displacement with ![]() (Section 2.1 )
to a
(Section 2.1 )
to a ![]() confidence level, i.e.
confidence level, i.e. ![]() . As for the thermal noise, laboratory tests
have yielded:
. As for the thermal noise, laboratory tests
have yielded:
![]()
and therefore, since ![]() , the differential displacement
, the differential displacement ![]() due to thermal noise is:
due to thermal noise is:
![]()
This means that the measurement accuracy required by the experiment can be achieved with
an integration time of about ![]() .
Thus, it is ruled out for the GG experiment be limited by the performances of the
capacitance read out. Care should be taken in keeping parasitic capacitances small.
However, since they depend on the geometry of the system, the resulting perturbation will
be DC. It is therefore enough to make sure that their effect does not exceed the
sensitivity by several orders of magnitude. It must be stressed that the required accuracy
of
.
Thus, it is ruled out for the GG experiment be limited by the performances of the
capacitance read out. Care should be taken in keeping parasitic capacitances small.
However, since they depend on the geometry of the system, the resulting perturbation will
be DC. It is therefore enough to make sure that their effect does not exceed the
sensitivity by several orders of magnitude. It must be stressed that the required accuracy
of ![]() refers to relative
displacements - at the spin frequency - of the centres of mass of the test bodies, not to
their surface irregularities. The latter will only give DC effects.
refers to relative
displacements - at the spin frequency - of the centres of mass of the test bodies, not to
their surface irregularities. The latter will only give DC effects.
It is apparent from Eq. 48 that for the read out
to be sensitive to the displacement caused by a possible EP violation of ![]() the corresponding
(differential) signal must be larger than the signal due to the largest possible
displacement in common mode. Namely:
the corresponding
(differential) signal must be larger than the signal due to the largest possible
displacement in common mode. Namely:
![]()
where ![]() and the
maximum common mode displacement is due to air drag and amounts to
and the
maximum common mode displacement is due to air drag and amounts to ![]() . Hence, the system must be balanced
to
. Hence, the system must be balanced
to ![]() , which
means
, which
means ![]() Ĺ. This level of balancing
can be achieved actively by means of inch-worm piezoelectric actuators (Fig.
17 ) acting on the mechanical support of each capacitance plate to make their distance
from the test masses as equal as possible. Inch-worm actuators are made of a combination
of piezoceramics (no magnets) and can achieve relatively large displacements by a
succession of very fine steps. Two inch-worms are needed for each plate, as shown in Fig. 2 . The driving signal for this active balancing is a constant
voltage obtained by a proper analysis of the
Ĺ. This level of balancing
can be achieved actively by means of inch-worm piezoelectric actuators (Fig.
17 ) acting on the mechanical support of each capacitance plate to make their distance
from the test masses as equal as possible. Inch-worm actuators are made of a combination
of piezoceramics (no magnets) and can achieve relatively large displacements by a
succession of very fine steps. Two inch-worms are needed for each plate, as shown in Fig. 2 . The driving signal for this active balancing is a constant
voltage obtained by a proper analysis of the ![]() signal. There is no danger to cancel an EP violation signal by actually
making a and b different because the largest common mode effect - which is
due to air drag - is variable in time. In any case, a phase check is able to tell whether
the signal is due to air drag or EP violation. Inch-worms with 1 Ĺ stepsize are
commercially available.
signal. There is no danger to cancel an EP violation signal by actually
making a and b different because the largest common mode effect - which is
due to air drag - is variable in time. In any case, a phase check is able to tell whether
the signal is due to air drag or EP violation. Inch-worms with 1 Ĺ stepsize are
commercially available.
Fig. 17. Scheme of the inch-worm. Lateral piezoelectric actuators alternately fasten and release the extremities of the inch-worm to the sides of its container while the inner part is made to expand and contract by means of the other piezoelectrics. In this way the inch-worm can move on a relatively long path in successive very small steps.
We now consider the electrostatic force which affects each test mass.
Let's take the inner test mass in the concentric initial configuration of Fig. 15 . As the mass moves by an amount x it is subject to an
average force ![]() given
by:
given
by:
![]()
This means that the electric forces simulate a spring with a negative constant ![]()
![]()
which could in principle be used to increase the displacement produced by the signal and
to reduce the natural frequency of the test masses, which would in turn reduce the
integration time because of the smaller thermal noise effect (Section 6.2 ). However, since the coupled suspension of
the test masses with gimbals appears to give a rather low natural frequency this
possibility needs not to be exploited.
Although a more detailed analysis is needed we conclude that a
capacitance read out system can reach the required precision of ![]() (corresponding to a
(corresponding to a ![]() confidence level in the displacement due to
an EP violation with
confidence level in the displacement due to
an EP violation with ![]() )
in a very short time and is therefore by far adequate to the task. It is also worth
stressing that ground tests of the capacitance read out system are possible, not only for
the sensitivity of the circuit, but also for the balancing and corresponding reduction of
the common mode displacements. We are working on a laboratory experiment with concentric,
cylindrical test masses in high speed supercritical rotation and a capacitance read out
like the one envisaged for GG. It would be a ground test of the main components of the
space experiment as well as, possibly, a valuable EP experiment in its own right.
)
in a very short time and is therefore by far adequate to the task. It is also worth
stressing that ground tests of the capacitance read out system are possible, not only for
the sensitivity of the circuit, but also for the balancing and corresponding reduction of
the common mode displacements. We are working on a laboratory experiment with concentric,
cylindrical test masses in high speed supercritical rotation and a capacitance read out
like the one envisaged for GG. It would be a ground test of the main components of the
space experiment as well as, possibly, a valuable EP experiment in its own right.
Test bodies are neither point like nor spherical. Therefore any source mass (e.g. the
Earth and the spacecraft body) will interact with their mass moments (higher than the
monopole) giving rise to differential effects between test masses. In the case of the
Earth, because of the ![]() rotation of
the test masses and the sensors, the effect will have this frequency, just like an EP
violation. On the contrary, when the source is an unbalanced spacecraft mass the effect is
DC because both the source and the test mass spin at the same rate. Let us compute the
quadrupole acceleration due to the Earth (regarded as a point mass) on a test body in the
shape of hollow cylinder with inner radius a, outer radius b, height L,
a fractional difference
rotation of
the test masses and the sensors, the effect will have this frequency, just like an EP
violation. On the contrary, when the source is an unbalanced spacecraft mass the effect is
DC because both the source and the test mass spin at the same rate. Let us compute the
quadrupole acceleration due to the Earth (regarded as a point mass) on a test body in the
shape of hollow cylinder with inner radius a, outer radius b, height L,
a fractional difference ![]() between its principal moments of inertia and the symmetry axis at an
angle
between its principal moments of inertia and the symmetry axis at an
angle ![]() with respect to the normal to
the orbit plane (
with respect to the normal to
the orbit plane (![]() at most a few degrees).
We get:
at most a few degrees).
We get:
![]()
in the plane of symmetry of the cylinder (the effect along the symmetry axis is from 10 to
100 times smaller). The function ![]() is about 1 for small
is about 1 for small ![]() .
For two concentric test cylinders of equal mass, the dimensions and
.
For two concentric test cylinders of equal mass, the dimensions and ![]() will be in general different,
thus giving rise to a differential effect in competition with an EP violation signal. We
have checked that in the 3-chamber setup of Fig. 1 which was used for
the finite element numerical stability analysis presented in Section
3 (equal composition bodies in the central chamber, different composition bodies in
the others) the resulting value of the quadrupole acceleration given by Eq.
55 is for all bodies at least one order of magnitude smaller than the expected
signal
will be in general different,
thus giving rise to a differential effect in competition with an EP violation signal. We
have checked that in the 3-chamber setup of Fig. 1 which was used for
the finite element numerical stability analysis presented in Section
3 (equal composition bodies in the central chamber, different composition bodies in
the others) the resulting value of the quadrupole acceleration given by Eq.
55 is for all bodies at least one order of magnitude smaller than the expected
signal ![]() . Evidently,
their differences in each chamber will also be below the signal. We therefore did not
devote any effort to making the numerical value of the quantity
. Evidently,
their differences in each chamber will also be below the signal. We therefore did not
devote any effort to making the numerical value of the quantity ![]() equal for the two masses. It
is worth noticing that the values of
equal for the two masses. It
is worth noticing that the values of ![]() (see Table 1 ) are not too small (from a few
percents to
(see Table 1 ) are not too small (from a few
percents to ![]() ) in order to avoid
additional instabilities.
) in order to avoid
additional instabilities.
As for the interaction of an unbalanced mass of the spacecraft with the quadrupole moment of a test body, we note that despite a much smaller source mass this effect is in fact larger because of its dependence on the fourth inverse power of the distance. However, it is constant because of the spinning of both the spacecraft and the test masses at the same frequency.
In any small force gravitational experiment electric charges on the test bodies must be
absolutely avoided since they can easily produce forces far much bigger than the
gravitational signal. The GG spacecraft does not contain free floating masses, and
therefore no electrostatic charges will be able to build up inside it. Potential
differences between the test masses can be avoided by coating them with a thin layer of
the same conductive material. The PGB laboratory can be made of ![]() , or another highly conductive material, so
as to work as a Faraday cage, shielding the experiment from external electric fields. Any
small residual charge inside the spacecraft will only produce a constant effect on the
output signal and can therefore be neglected. It is worth stressing that this is a very
important advantage of GG as compared to STEP, where the test bodies are suspended by
means of magnetic bearings and the problem of discharging them without producing unwanted
perturbations is a serious one. The problem is even worse if the spacecraft orbit goes, as
in the case of STEP, through the Van Allen belts and is subject to the bombardment of
charged particles in the so-called South Atlantic Anomaly. The orbit of GG is equatorial
and at a low enough altitude to avoid the South Atlantic Anomaly.
, or another highly conductive material, so
as to work as a Faraday cage, shielding the experiment from external electric fields. Any
small residual charge inside the spacecraft will only produce a constant effect on the
output signal and can therefore be neglected. It is worth stressing that this is a very
important advantage of GG as compared to STEP, where the test bodies are suspended by
means of magnetic bearings and the problem of discharging them without producing unwanted
perturbations is a serious one. The problem is even worse if the spacecraft orbit goes, as
in the case of STEP, through the Van Allen belts and is subject to the bombardment of
charged particles in the so-called South Atlantic Anomaly. The orbit of GG is equatorial
and at a low enough altitude to avoid the South Atlantic Anomaly.
Fig. 18. In an equatorial orbit the direction of the Earth's magnetic field is not more than about
away from the perpendicular to the orbit. Therefore its effects in the plane of the orbit will be reduced to about
times those of the full field. These effects are distinguishable from a violation of the equivalence principle because they change sign every half orbit.
Magnetic disturbances can be of two types: interactions of magnetized
or magnetizable materials between themselves and interactions between these materials and
the Earth's magnetic field. All magnetic and especially ferromagnetic materials inside the
spacecraft should be avoided, i.e. magnets, electromagnets and electric motors. All
electric currents should flow in shielded cables. For small controlled displacements we
shall use piezoelectric actuators and active damping will be realized with electrostatic
actuators. Any residual constant magnetization inside the spacecraft, as for the case of
electrostatic charges, would produce only a DC effect (unless there is a relative motion
at the spinning frequency). If the GG satellite is essentially non magnetic, its attitude
is almost unaffected by the Earth's magnetic field ![]() because on average over one orbit
because on average over one orbit ![]() is almost parallel to the spin axis. Along the satellite orbit the
instantaneous orientation of
is almost parallel to the spin axis. Along the satellite orbit the
instantaneous orientation of ![]() is no
more than about
is no
more than about ![]() away from the spin
axis of the satellite (Fig. 18 ). Thus, the component of
away from the spin
axis of the satellite (Fig. 18 ). Thus, the component of ![]() in the orbit plane can only produces a
signal whose amplitude is reduced by a factor
in the orbit plane can only produces a
signal whose amplitude is reduced by a factor ![]() . If the interaction is between the proper test
mass magnetization and the Earth's magnetic field, the frequency of this signal is
. If the interaction is between the proper test
mass magnetization and the Earth's magnetic field, the frequency of this signal is ![]() , because the shape of the
magnetic field rotates with the Earth. The signal also changes sign every half orbit of
the satellite. When the interaction is between induced magnetization on the test mass and
the Earth's magnetic field, the frequency is
, because the shape of the
magnetic field rotates with the Earth. The signal also changes sign every half orbit of
the satellite. When the interaction is between induced magnetization on the test mass and
the Earth's magnetic field, the frequency is ![]() because it depends on
because it depends on ![]() . We can argue in the same way for the
component of
. We can argue in the same way for the
component of ![]() parallel to the spin
axis. The interaction between magnetized test masses gives an
parallel to the spin
axis. The interaction between magnetized test masses gives an ![]() signal only if the
interaction is between an induced magnetized test mass and a test mass with its own
magnetization. A signal at this frequency could also arise if the test masses have their
own magnetization and are subject to deformations (e.g. due to nonuniform thermal
expansion) at the
signal only if the
interaction is between an induced magnetized test mass and a test mass with its own
magnetization. A signal at this frequency could also arise if the test masses have their
own magnetization and are subject to deformations (e.g. due to nonuniform thermal
expansion) at the ![]() frequency.
frequency.
Let us now estimate the intensity of these perturbations. The most
dangerous ones are those which act at (or close to) the spin/signal frequency. The largest
among them is due to the interaction between the magnetic moment ![]() (due to ferromagnetic
impurities) of one test body and the magnetization induced on the other (with
susceptibility
(due to ferromagnetic
impurities) of one test body and the magnetization induced on the other (with
susceptibility ![]() ) by
the magnetic field of the Earth. In the worst case hypotheses the resulting perturbing
force which competes with the signal is (in MKS):
) by
the magnetic field of the Earth. In the worst case hypotheses the resulting perturbing
force which competes with the signal is (in MKS):
![]()
with ![]() (
(![]() the permeability of
vacuum),
the permeability of
vacuum), ![]() ,
, ![]() the mutual distance and
the mutual distance and ![]() the volume of body 1. For it
to be smaller than the signal
the volume of body 1. For it
to be smaller than the signal ![]() it must be:
it must be:
![]()
Since reasonable values for the susceptibility are ![]() , we need
, we need ![]() . From experimental data reported in textbooks we find that the
magnetic moment of a cube of magnet of
. From experimental data reported in textbooks we find that the
magnetic moment of a cube of magnet of ![]() size is about
size is about ![]() . Since
this is in fact quite a large impurity, it appears that the inequality (Eq.
59 ) can be satisfied by the test bodies thus ruling out any need of reducing the
magnetic field of the Earth inside the satellite. Another magnetic perturbation which acts
at the spin/signal frequency is due to the interaction of the magnetic moment of one test
body with the magnetic field of the Earth. Worst case hypotheses give:
. Since
this is in fact quite a large impurity, it appears that the inequality (Eq.
59 ) can be satisfied by the test bodies thus ruling out any need of reducing the
magnetic field of the Earth inside the satellite. Another magnetic perturbation which acts
at the spin/signal frequency is due to the interaction of the magnetic moment of one test
body with the magnetic field of the Earth. Worst case hypotheses give:
![]()
hence we need ![]() ,
which can be easily satisfied. A DC magnetic perturbation comes from the interaction of
the magnetic moments of two test bodies with one another:
,
which can be easily satisfied. A DC magnetic perturbation comes from the interaction of
the magnetic moments of two test bodies with one another:
![]()
For it to be smaller than the signal it must be ![]() , which, from the previous discussion, is a
reasonable requirement for a DC effect. We complete the analysis by estimating the
magnetic perturbations which contain
, which, from the previous discussion, is a
reasonable requirement for a DC effect. We complete the analysis by estimating the
magnetic perturbations which contain ![]() and therefore appear at a frequency close to twice the spin/signal frequency.
One of these effects is due to the interaction of the magnetic moments induced on the test
bodies with one another:
and therefore appear at a frequency close to twice the spin/signal frequency.
One of these effects is due to the interaction of the magnetic moments induced on the test
bodies with one another:
![]()
which requires ![]() and
is satisfied because
and
is satisfied because ![]() .
Another
.
Another ![]() effect comes from the
interaction between B and the magnetization induced on a test body by B
itself. The resulting perturbation force is:
effect comes from the
interaction between B and the magnetization induced on a test body by B
itself. The resulting perturbation force is:
![]()
and it is smaller than the signal provided that ![]() , which is surely the case.
, which is surely the case.
In conclusion, as far as magnetic perturbations in the GG experiment
are considered, we have demonstrated that the only one which sets a somewhat demanding
requirement is due to the coupling of the magnetic field of the Earth with the magnetic
moment of either test body due to residual ferromagnetic impurities. For this effect to be
neglected we need the magnetic moment of the test bodies not to exceed a few ![]() , which appears to be feasible. On the
contrary, in the torsion balance of the Eöt-Wash experiment (Su, 1992; Su et al.,
1994) the magnetic field of the Earth near the balance was reduced by a total factor
of
, which appears to be feasible. On the
contrary, in the torsion balance of the Eöt-Wash experiment (Su, 1992; Su et al.,
1994) the magnetic field of the Earth near the balance was reduced by a total factor
of ![]() (partly with
(partly with ![]() -metal shielding, partly with
Helmotz coils). This seems to contradict our previous conclusion, especially if one
considers that they have reached a sensitivity
-metal shielding, partly with
Helmotz coils). This seems to contradict our previous conclusion, especially if one
considers that they have reached a sensitivity ![]() while the GG target is
while the GG target is ![]() . Indeed, it is not so and we
are going to show why. The first important fact to bear in mind is that, despite its
higher target sensitivity the GG expected force signal is
. Indeed, it is not so and we
are going to show why. The first important fact to bear in mind is that, despite its
higher target sensitivity the GG expected force signal is ![]() times larger than it is in Eöt-Wash, because of the bigger EP
signal in space and the larger mass of the test bodies. In GG there are two test bodies
of
times larger than it is in Eöt-Wash, because of the bigger EP
signal in space and the larger mass of the test bodies. In GG there are two test bodies
of ![]() each while in
the Eöt-Wash torsion balance there are 4 masses of
each while in
the Eöt-Wash torsion balance there are 4 masses of ![]() each; the force signals are
each; the force signals are ![]() and
and ![]() respectively. Note that the force, not the acceleration, is
relevant when dealing with nongravitational perturbations. Secondly, since the Eöt-Wash
experiment is a torsion balance experiment it is sensitive to torques, hence also to the
magnetic torque generated by the interaction of the magnetic field of the Earth with
magnetic moments of the test bodies (due to residual ferromagnetic impurities). Indeed, it
turns out that the magnetic moment of the tray on which the test bodies are positioned
gives an even larger perturbation than the test masses themselves. For this torque to be
smaller than that due to an EP violation it must be:
respectively. Note that the force, not the acceleration, is
relevant when dealing with nongravitational perturbations. Secondly, since the Eöt-Wash
experiment is a torsion balance experiment it is sensitive to torques, hence also to the
magnetic torque generated by the interaction of the magnetic field of the Earth with
magnetic moments of the test bodies (due to residual ferromagnetic impurities). Indeed, it
turns out that the magnetic moment of the tray on which the test bodies are positioned
gives an even larger perturbation than the test masses themselves. For this torque to be
smaller than that due to an EP violation it must be:
![]()
where ![]() is the length of the arm. It
must therefore be
is the length of the arm. It
must therefore be ![]() (having used
(having used ![]() as above, although
the value used by Su et al. (1994) is
actually
as above, although
the value used by Su et al. (1994) is
actually ![]() ). From measurement of
the torsion angle in absence of any shielding or coils the Eöt-Wash group finds that the
residual magnetic moment of the tray (made of Al) is
). From measurement of
the torsion angle in absence of any shielding or coils the Eöt-Wash group finds that the
residual magnetic moment of the tray (made of Al) is ![]() (Su, 1992; Su et al., 1994), thus making a reduction of B
by
(Su, 1992; Su et al., 1994), thus making a reduction of B
by ![]() crucial for the success of the
experiment. This is achieved by means of a 3-layer
crucial for the success of the
experiment. This is achieved by means of a 3-layer ![]() -metal shielding for a factor
-metal shielding for a factor ![]() and of Helmotz coils for a factor 28. As for
the Eöt-Wash test masses, the measured value of the residual magnetic moment is
and of Helmotz coils for a factor 28. As for
the Eöt-Wash test masses, the measured value of the residual magnetic moment is ![]() while the requirement imposed by the
magnetic torque is about
while the requirement imposed by the
magnetic torque is about ![]() ; with a
factor
; with a
factor ![]() of reduction of the
magnetic field of the Earth made necessary by the tray, this effect is no problem. The
magnetic dampers, used to kill the swing and wobble modes so that the motor can provide a
smooth rotation, will also benefit of the reduction of the magnetic field. In GG we have
symmetric and concentric masses and the signal is a force, not a torque, thus we have
nothing like the torque (Eq. 62 ); we do not have any motor or
magnetic dampers either.
of reduction of the
magnetic field of the Earth made necessary by the tray, this effect is no problem. The
magnetic dampers, used to kill the swing and wobble modes so that the motor can provide a
smooth rotation, will also benefit of the reduction of the magnetic field. In GG we have
symmetric and concentric masses and the signal is a force, not a torque, thus we have
nothing like the torque (Eq. 62 ); we do not have any motor or
magnetic dampers either.
All space experiments which involve freely falling or softly suspended bodies require
them to be locked during launch, and properly unlocked once in orbit to start the
experiment. First of all we find it important to avoid any danger of the payload hitting
the spacecraft walls. This is done simply by having each suspended mass and the PGB
laboratory constrained to only slight movements by means of mechanical stops. Gaps of a
few millimetres in size make the very soft mechanical suspension dominate during the
experimental phase but at the same time constrain the body to within a small range of
movements in case anything unpredictable should happen. As for the launch phase, when the
system is subject to strong accelerations, we envisage having a static mechanical locking
for each body, typically made of 3 lockers ![]() apart on each suspension side. As for the forces acting on the springs
themselves during launch, we recall that their mass is very small; it is also possible to
use mechanical stops in order to avoid large displacements. Estimates show that there is
no danger for the elasticity regime to be exceeded during launch, even though some time
for relaxation should probably be allowed at the beginning of the mission. Once the
spacecraft has been injected in its orbit and given the required attitude and spin rate
the static mechanical lockers can be released and never used again. A symmetrical locking
consisting of 4 inch-worms placed at
apart on each suspension side. As for the forces acting on the springs
themselves during launch, we recall that their mass is very small; it is also possible to
use mechanical stops in order to avoid large displacements. Estimates show that there is
no danger for the elasticity regime to be exceeded during launch, even though some time
for relaxation should probably be allowed at the beginning of the mission. Once the
spacecraft has been injected in its orbit and given the required attitude and spin rate
the static mechanical lockers can be released and never used again. A symmetrical locking
consisting of 4 inch-worms placed at ![]() from one another as shown in Fig. 19 is provided, each
inch-worm being equipped with a force sensor sensitive to
from one another as shown in Fig. 19 is provided, each
inch-worm being equipped with a force sensor sensitive to ![]() . It gives a measure of the centrifugal force in
that direction, and therefore provides the driving signal to the inch-worms for reducing
the distance offset from the rotation axis. Once this has been reduced to
. It gives a measure of the centrifugal force in
that direction, and therefore provides the driving signal to the inch-worms for reducing
the distance offset from the rotation axis. Once this has been reduced to ![]() , which means a centrifugal force of
, which means a centrifugal force of ![]() for the suspended test
masses, active centering with inch-worms can be stopped; the electrostatic dampers will
then stabilize whirling and precessional motions around the equilibrium position of
supercritical rotation as shown in Section 3 . While the
static lockers are meant not to be reused, the inch-worms can. Together with the
mechanical stops they make the system in principle safe from unexpected occurrences.
for the suspended test
masses, active centering with inch-worms can be stopped; the electrostatic dampers will
then stabilize whirling and precessional motions around the equilibrium position of
supercritical rotation as shown in Section 3 . While the
static lockers are meant not to be reused, the inch-worms can. Together with the
mechanical stops they make the system in principle safe from unexpected occurrences.
Fig. 19. Top view of a set of four inch-worms actuators for locking and unlocking the suspended masses. Each mass needs two such sets placed at its two axial ends (see also Fig. 2 ). Between the inch-worms are the electrostatic plates used for active damping. The rod, hence the suspended masses, is locked during launch and until the spacecraft has reached the final spin angular velocity
. Then the inch-worms equipped with pressure sensors sensitive to
are used for initial centering until the centrifugal forces detected by the pressure sensors become smaller than the forces that can be generated by the electrostatic plates. At this point the inch-worm will be retracted and the electrostatic system will complete the centering and will keep it stable.
General Relativity and all metric theories of gravity rely on the principle of
equivalence between inertial and gravitational mass. Its fundamental character and far
reaching implications make it necessary for it to be tested as accurately as possible by
testing the Universality of Free Fall. If the test bodies orbit around the Earth
the signal is about 3 orders of magnitude bigger than at its surface, and this is what
makes space experiments to test the equivalence principle so attractive despite their
inevitable difficulties. We have presented here a nondrag-free version of the Galileo
Galilei (GG) mission proposal, arguing that it could detect any deviation from the Universality
of Free Fall - hence from the equivalence between inertial and gravitational mass - to
the level of 1 part in ![]() , four
orders of magnitude better than the most recent ground tests (Adelberger et al., 1990; Su et al., 1994). The main features of this concept
are to be nondrag-free and non cryogenic, to make the test bodies spin at a relatively
high frequency chosen by the experimentalist (e.g.
, four
orders of magnitude better than the most recent ground tests (Adelberger et al., 1990; Su et al., 1994). The main features of this concept
are to be nondrag-free and non cryogenic, to make the test bodies spin at a relatively
high frequency chosen by the experimentalist (e.g. ![]() ) and to exploit the zero-g space environment in order to
naturally obtain self-centering of the test bodies and a very low level of vibrational
noise. The spacecraft is small, compact and essentially passive so as to minimize
disturbances on the test masses; no active control, neither of the orbit nor of the
attitude is needed. The signal from a violation of equivalence would be modulated at the
spin frequency of the test bodies (and the spacecraft) while the common rotation of the
entire apparatus makes many internal perturbing effects DC. The read out system is
capacitive. In the perturbation analysis we have tried to keep all directly competing
effects well below the target signal unless otherwise distinguishable. Thermal
perturbations can be sufficiently reduced by passive insulation thanks to fast spin and
vacuum. It is concluded that a violation of equivalence to the level of 1 part in
) and to exploit the zero-g space environment in order to
naturally obtain self-centering of the test bodies and a very low level of vibrational
noise. The spacecraft is small, compact and essentially passive so as to minimize
disturbances on the test masses; no active control, neither of the orbit nor of the
attitude is needed. The signal from a violation of equivalence would be modulated at the
spin frequency of the test bodies (and the spacecraft) while the common rotation of the
entire apparatus makes many internal perturbing effects DC. The read out system is
capacitive. In the perturbation analysis we have tried to keep all directly competing
effects well below the target signal unless otherwise distinguishable. Thermal
perturbations can be sufficiently reduced by passive insulation thanks to fast spin and
vacuum. It is concluded that a violation of equivalence to the level of 1 part in ![]() can be detected with an integration time of
a few hours. A partial compensation of air drag would help reduce the intensity of
inertial forces on test bodies and - correspondingly - the required level of common mode
rejection. However, drag-free control is advantageous only if the thrusters are
proportional rather than impulsive and the propellant to be carried on board does not
itself give rise to perturbations. An interesting possibility would be to use FEEP (Field
Emission Electric Propulsion) thrusters, which need a negligible amount of Cesium and are
meant to be highly proportional. A drag-free GG mission with FEEP thrusters (Nobili et al., 1995; GALILEO GALILEI, 1996) can indeed aim at a 1
order of magnitude better sensitivity, i.e. at an EP test to 1 part in
can be detected with an integration time of
a few hours. A partial compensation of air drag would help reduce the intensity of
inertial forces on test bodies and - correspondingly - the required level of common mode
rejection. However, drag-free control is advantageous only if the thrusters are
proportional rather than impulsive and the propellant to be carried on board does not
itself give rise to perturbations. An interesting possibility would be to use FEEP (Field
Emission Electric Propulsion) thrusters, which need a negligible amount of Cesium and are
meant to be highly proportional. A drag-free GG mission with FEEP thrusters (Nobili et al., 1995; GALILEO GALILEI, 1996) can indeed aim at a 1
order of magnitude better sensitivity, i.e. at an EP test to 1 part in ![]() . As for the possibility to run the
experiment at low temperature, the advantages must be weighed against the disturbances due
to the cryogenic system itself. Taking also into account that a room temperature
capacitive read out is adequate to the task, we have preferred to consider a non cryogenic
experiment. The choice for a space mission completely devoted to one single scientific
objective (indeed the entire spacecraft, its orbit and attitude control are driven by this
objective) was done on purpose, to reduce the complexity, cost and realization time were
any space agency interested in the experiment. To this end it is worth stressing that the
major components of the space experiment can be tested in the ground laboratory, and even
though the entire apparatus is designed for zero g a modified, less accurate (due
to the weaker signal), 1-g version of it is possible and is underway.
. As for the possibility to run the
experiment at low temperature, the advantages must be weighed against the disturbances due
to the cryogenic system itself. Taking also into account that a room temperature
capacitive read out is adequate to the task, we have preferred to consider a non cryogenic
experiment. The choice for a space mission completely devoted to one single scientific
objective (indeed the entire spacecraft, its orbit and attitude control are driven by this
objective) was done on purpose, to reduce the complexity, cost and realization time were
any space agency interested in the experiment. To this end it is worth stressing that the
major components of the space experiment can be tested in the ground laboratory, and even
though the entire apparatus is designed for zero g a modified, less accurate (due
to the weaker signal), 1-g version of it is possible and is underway.
Copyright © 1998 Elsevier Science B.V., Amsterdam. All Rights Reserved.
![]()
![]()
![]()
(Anna Nobili- nobili@dm.unipi.it)
Last edited May 14, 1998