![]()
Let now the two bodies of the oscillator be concentric cylinders rotating with angular
velocity ![]() . Assume that they are mechanically coupled by a spring with a stiffness k
so small that the natural frequency of relative oscillation
. Assume that they are mechanically coupled by a spring with a stiffness k
so small that the natural frequency of relative oscillation ![]() is much smaller than
is much smaller than ![]() . It
is known that in this case each body rotates around its own symmetry axis and there is a
position of relative equilibrium (fixed in the rotating frame) very close to the spin
axis. Assume for the time being perfect centring (i.e. the equilibrium position lies
exactly on the spin axis).
. It
is known that in this case each body rotates around its own symmetry axis and there is a
position of relative equilibrium (fixed in the rotating frame) very close to the spin
axis. Assume for the time being perfect centring (i.e. the equilibrium position lies
exactly on the spin axis).
If there is friction inside rotating parts of the system (e.g. the springs) this
amounts to a non-zero rotating damping which has to be taken into account in the
equations of motion. Rotating damping has a destabilizing effect because it produces a
spin down of the system and a corresponding (forward) whirling motion of the rotating
bodies around their common centre of mass, with an exponentially increasing amplitude. The
angular frequency of whirl ![]() depends on the kind of rotating damping
present in the system. Let Q represent the total dissipation of the system due to
friction inside its rotating parts. We can distinguish between structural damping and
viscous damping. Structural damping (also known as hysteresis damping) is due to the
relative motions of different parts in the material when subject to deformations (the
springs); the particles maintain essentially their relative positions and the motions are
due to the deformations. Instead, viscous damping occurs between particles sliding the
ones with respect to the others.
depends on the kind of rotating damping
present in the system. Let Q represent the total dissipation of the system due to
friction inside its rotating parts. We can distinguish between structural damping and
viscous damping. Structural damping (also known as hysteresis damping) is due to the
relative motions of different parts in the material when subject to deformations (the
springs); the particles maintain essentially their relative positions and the motions are
due to the deformations. Instead, viscous damping occurs between particles sliding the
ones with respect to the others.
The frequency of whirl is computed by solving the equations of motion with rotating friction in the system being of structural nature and of viscous nature (see Appendix).
In the case of rotating structural friction we find (using ![]() ) a whirling angular
frequency:
) a whirling angular
frequency:

yielding, for ![]() ,
,
![]()
That is, the frequency of the destabilizing (forward) whirling motion is essentially
the natural frequency of the system. In the case of rotating viscous friction, expressed
by a quality factor ![]() of the system, we consider, for a rotor
with a given ratio
of the system, we consider, for a rotor
with a given ratio ![]() , three subcases: of very small,
intermediate and very large viscous damping, namely:
, three subcases: of very small,
intermediate and very large viscous damping, namely: ![]() ;
; ![]() ;
; ![]() ;.
The resulting whirling frequencies are:
;.
The resulting whirling frequencies are:
![]()
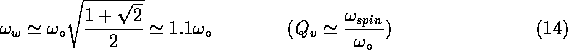
![]()
It is therefore apparent that, unless the system has a very large coefficient of
rotating damping due to viscous friction (with a viscous quality factor much smaller than
the ratio spin-to-natural frequency) the frequency of the whirling (destabilizing), motion
is close to the natural frequency of the system (Eqs. (13) and (14)). A small amount of
viscous damping does not change the frequency of whirl in any significant way with respect
to the case in which only structural damping is present, while in the presence of a very
large viscous damping it would be ![]() . In the GG experiment we can certainly
exclude the presence of very large viscous friction (see Appendix), and therefore it is
. In the GG experiment we can certainly
exclude the presence of very large viscous friction (see Appendix), and therefore it is ![]() .
.
We can now compute the quality factor ![]() of the whirling motion, which is defined by
the equation:
of the whirling motion, which is defined by
the equation:
![]()
where now
![]()
because ![]() increases with time as the whirling motion gains angular momentum,
necessarily from the spin angular momentum of the rotor. Consider a system of two
concentric hollow cylindrical rotors, each of mass m (section across the spin
axis), coupled by weak springs and rotating at
increases with time as the whirling motion gains angular momentum,
necessarily from the spin angular momentum of the rotor. Consider a system of two
concentric hollow cylindrical rotors, each of mass m (section across the spin
axis), coupled by weak springs and rotating at ![]() (Fig. 1). They develop a forward whirling
motion of radius
(Fig. 1). They develop a forward whirling
motion of radius ![]() around the common centre of mass O and at angular frequency
around the common centre of mass O and at angular frequency ![]() (
( ![]() except in the presence of very large viscous friction in which case it is
except in the presence of very large viscous friction in which case it is ![]() ). For our
calculations the elastic properties of the system can be represented by a spring
subdivided into 4 springs at
). For our
calculations the elastic properties of the system can be represented by a spring
subdivided into 4 springs at ![]() from one another, each with longitudinal
stiffness k/4. This system of springs is equivalent to two springs with stiffness k/2
coupling the two masses in both the x and y directions.
from one another, each with longitudinal
stiffness k/4. This system of springs is equivalent to two springs with stiffness k/2
coupling the two masses in both the x and y directions.
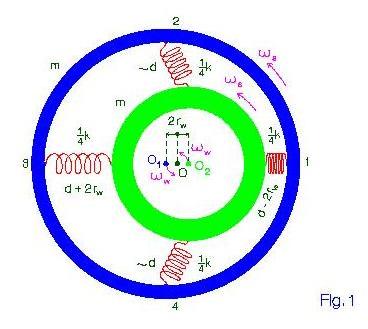
Figure 1: Section across the spin axis of the system of two hollow
cylindrical masses coupled by weak springs. Both masses are spinning at the same angular
velocity ![]() around their respective centres of mass
around their respective centres of mass ![]() and
and ![]() . In their turn
. In their turn ![]() and
and ![]() are
"whirling" around the centre of mass O of the whole system, at a distance
are
"whirling" around the centre of mass O of the whole system, at a distance
![]() and
at the angular velocity
and
at the angular velocity ![]() .
.
The time variation of the spin angular velocity of the system can be computed from the conservation of the total angular momentum, namely the angular momentum of spin:
![]()
(R is the linear dimension of the rotor) plus the angular momentum of the whirling motion:
![]()
It must be:
![]()
Hence:
![]()
From (16) the rate of growth ![]() is:
is:
![]()
and the corresponding despin rate of the rotor is:
![]()
which gives the time variation of the spin angular velocity of the rotor in terms of the ``negative'' dissipation of the whirling motion.
Let us now consider the energy of the system. Since the springs are very weak and their
masses are negligible compared to the mass of the rotor (see Fig. 1), they will be obliged
to follow the motion of the attachement points which rotate at ![]() around the centre of mass of
the respective test mass. The centres of mass of the springs will rotate around O
at
around the centre of mass of
the respective test mass. The centres of mass of the springs will rotate around O
at ![]() . When the springs are going from position 1 to position 3 (see Fig. 1) they will be
forced to expand by
. When the springs are going from position 1 to position 3 (see Fig. 1) they will be
forced to expand by ![]() , and when going from position 3 to 1 to
contract by the same amount. In the figure the four position numbers represent the phase
of the whirling motion, in
, and when going from position 3 to 1 to
contract by the same amount. In the figure the four position numbers represent the phase
of the whirling motion, in ![]() steps, with position 1 always in the
direction
steps, with position 1 always in the
direction ![]() . They rotate around O with angular frequency
. They rotate around O with angular frequency ![]() . After the
spring, starting from position 1, has completed one turn in the time
. After the
spring, starting from position 1, has completed one turn in the time ![]() , the whirling
motion will have displaced position 1 by an angle
, the whirling
motion will have displaced position 1 by an angle ![]() (The + sign refers to the
forward whirling and the - to the backward one). Therefore, in order to reach again the
position 1 of maximum contraction, the spring takes a time
(The + sign refers to the
forward whirling and the - to the backward one). Therefore, in order to reach again the
position 1 of maximum contraction, the spring takes a time ![]() , slightly different from
, slightly different from ![]() . We
have
. We
have ![]() . This means that each spring is forced to oscillate with amplitude
. This means that each spring is forced to oscillate with amplitude ![]() at
the frequency
at
the frequency ![]() (The - sign is for the forward whirling and the + for the backward one).
We see that these are the only frequencies at which the springs are forced to oscillate
and that no deformations whatsoever take place in the spring's material at the whirling
frequency. This is rather counterintuitive, since it is just the opposite of what happens
in the more familiar case with
(The - sign is for the forward whirling and the + for the backward one).
We see that these are the only frequencies at which the springs are forced to oscillate
and that no deformations whatsoever take place in the spring's material at the whirling
frequency. This is rather counterintuitive, since it is just the opposite of what happens
in the more familiar case with ![]() , and since the two centers of mass
, and since the two centers of mass ![]() ,
, ![]() of
the two masses are seen (in the inertial reference frame) to rotate at
of
the two masses are seen (in the inertial reference frame) to rotate at ![]() one with respect
to the other. It would also be wrong to say that a deformation of the spring's material
with frequency
one with respect
to the other. It would also be wrong to say that a deformation of the spring's material
with frequency ![]() is superimposed to the one at
is superimposed to the one at ![]() : the only effect of
: the only effect of ![]() is to slightly
correct
is to slightly
correct ![]() into
into ![]() . In the general case of an elliptical
whirling motion (see Eqs. (1), (2), (3)) we have the superposition of the two dissipations
at two angular frequencies
. In the general case of an elliptical
whirling motion (see Eqs. (1), (2), (3)) we have the superposition of the two dissipations
at two angular frequencies ![]() and
and ![]() but still no dissipation at
but still no dissipation at ![]() .
These mechanical deformations are exactly the same as those of the one dimensional elastic
oscillator of Fig. 2 if this oscillator has an identical spring (with stiffness k/4)
and two small masses
.
These mechanical deformations are exactly the same as those of the one dimensional elastic
oscillator of Fig. 2 if this oscillator has an identical spring (with stiffness k/4)
and two small masses ![]() attached to its ends, with
attached to its ends, with ![]() so that its
frequency of oscillation has the same value
so that its
frequency of oscillation has the same value ![]() as in the rotor of Fig. 1, and if it is
made to oscillate with the same amplitude
as in the rotor of Fig. 1, and if it is
made to oscillate with the same amplitude ![]() . The energy of the oscillator will
decrease in time according to the law:
. The energy of the oscillator will
decrease in time according to the law:
![]()
which defines its quality factor ![]() and also defines the way by which
and also defines the way by which ![]() should be measured experimentally;
should be measured experimentally; ![]() accounts for all losses in the oscillator
at the frequency
accounts for all losses in the oscillator
at the frequency ![]() .
.
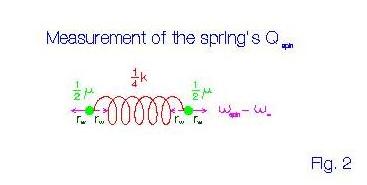
Figure 2: Measurement of the spring's quality factor ![]() at the frequency
at the frequency ![]() .
.
The time derivative of (24) yields:
![]()
where ![]() is the energy of the oscillator in Fig. 2. Hence:
is the energy of the oscillator in Fig. 2. Hence:
![]()
Since this oscillator has the same frequency and amplitude as each one of the 4 rotor's springs of Fig. 1, the total energy dissipated (as heat) inside the 4 rotor's springs is simply 4 times the energy dissipated by the oscillator of Fig. 2, that is:
![]()
which is nothing but the energy dissipated by the rotor because of rotatingdamping, i.e. because of friction between different parts of the rotor.
The conservation of energy requires that:
![]()
where:
![]()
is the spin energy of the rotor and:
![]()
the energy (kinetic + elastic) of the whirling motion of the system. Eq. (28) says that the energy dissipated inside the rotor's springs cannot result only in a spin down of the rotor (i.e. the spin energy of the rotor cannot decrease by exactly the same amount as the energy dissipated inside the springs) because the conservation of angular momentum requires the development of a whirling motion which will gain angular momentum as well as energy, while the springs do not enter in the balance of angular momentum. From (29), using (21), and from (30), we have:
![]()
that is:
![]()
which means that only the small fraction ![]() of the energy lost by the rotor is gained
by the whirling motion, all the rest being dissipated as heat in the springs (
of the energy lost by the rotor is gained
by the whirling motion, all the rest being dissipated as heat in the springs ( ![]() ).
From (28), using (27) for
).
From (28), using (27) for ![]() and (22) for
and (22) for ![]() (needed to compute the time
derivatives of (31)) we get:
(needed to compute the time
derivatives of (31)) we get:
![]()
By substituting Eq. (23) into Eq. (33) we obtain:
![]()
Clearly, the destabilizing (tangent) force along the whirling circle is (see (8) to (10)):
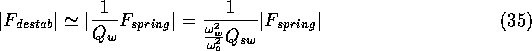
Apart for the case of very large viscous damping, Eq. (34) yields:
![]()
because ![]() ,
, ![]() (
( ![]() accounts for all dissipation
at the spin frequency). That is, the negative dissipation of the whirling (destabilizing)
motion is equal and opposite to the dissipation of the rotor's springs when forced to
oscillate at the spinning minus whirling frequency, which is essentially the spinning
frequency. And Eq. (35), with (36), becomes:
accounts for all dissipation
at the spin frequency). That is, the negative dissipation of the whirling (destabilizing)
motion is equal and opposite to the dissipation of the rotor's springs when forced to
oscillate at the spinning minus whirling frequency, which is essentially the spinning
frequency. And Eq. (35), with (36), becomes:
![]()
( ![]() and
and ![]() are at about
are at about ![]() ). Hence,
). Hence,
![]()
This result applies to the GG experiment where the presence of a very large viscous
damping ( ![]() ) can certainly be ruled out. Indeed, with a planned spinning frequency
of
) can certainly be ruled out. Indeed, with a planned spinning frequency
of ![]() , the quality factor
, the quality factor ![]() of the springs (which accounts for all
losses at the spin frequency) is certainly much larger than 1, and therefore the
destabilizing forces are much smaller (by far) than the spring forces. An active damping
force (servo force), opposite to
of the springs (which accounts for all
losses at the spin frequency) is certainly much larger than 1, and therefore the
destabilizing forces are much smaller (by far) than the spring forces. An active damping
force (servo force), opposite to ![]() and slightly larger will clearly stabilize
the system.
and slightly larger will clearly stabilize
the system.
In a rotating system dominated by a very large viscous damping it would be:

with ![]() ,
, ![]() and
and ![]() : even in this case the
destabilizing force generated by a very large amount of viscous friction is only a
fraction of the spring force. It is therefore not true that: ``A minimal level of
viscous damping has a serious effect on the performance estimate. The servo forces will
dominate the passive spring forces'', as stated by the FPAG reviewing panel of ESA
(resolution FPAG(96)4 of 9 October 1996, Point no. 2).
: even in this case the
destabilizing force generated by a very large amount of viscous friction is only a
fraction of the spring force. It is therefore not true that: ``A minimal level of
viscous damping has a serious effect on the performance estimate. The servo forces will
dominate the passive spring forces'', as stated by the FPAG reviewing panel of ESA
(resolution FPAG(96)4 of 9 October 1996, Point no. 2).
![]()
(Anna Nobili- nobili@dm.unipi.it)