2.2 Perturbation Analysis, Requirements and Error Budget
Chapter 2.2 Ready to Download and Print (0.2 MB): chapter2_2.pdf
2.2.1 Requirements on Drag Compensation and Balancing
The force due to atmospheric drag on low Earth spacecraft in near circular orbit depends on the solar cycle (it is maximum when solar activity is maximum) and oscillates every orbit between a minimum and a maximum because the iso-density surfaces of the atmosphere are not spherically symmetric around the Earth (there is an atmospheric bulge). For a GG mission starting at the beginning of 2002 (close to solar maximum) in its nominal near circular, near equatorial orbit at 520 km altitude and the spin axis close to the orbit normal, the maximum value at each orbit of the atmospheric drag force on the GG spacecraft, as evaluated according to the ESABASE software model (at
2s level) amounts to 65.18 m N. The corresponding (maximum) acceleration, which is transferred to the suspended bodies inside the spacecraft as shown in Sec. 2.1.4, amounts to![]() (2.36)
(2.36)
The drag force is the largest force that the spacecraft is subject to. Forces due to solar radiation, Earth albedo (the fraction of sunlight re-emitted by the Earth and hitting the spacecraft) and Earth infrared radiation, are all smaller (by at least a factor of
2). The value given above for the (maximum) air drag acceleration on GG close to solar maximum is a very small fraction (@ 2.7× 10-8) of the acceleration of gravity on the surface of the Earth, but it is also much larger (by a factor @ 2.5× 109) than the expected acceleration aEP @ 8.38× 10-17 m/sec2 caused by a violation of the Equivalence Principle at the level of 1 part in 1017 (as from Eq. (1.2)). This explains in simple terms why it must be easy to weakly couple and balance the GG test bodies in space; however, it also makes it apparent that the effect of drag is huge for the required sensitivity of the EP experiment and must therefore be dealt with very carefully, the only favorable features being (i) that the resulting effect of drag on the test bodies in inherently common mode (while the expected EP signal is differential); (ii) that its largest component is at about 90° from the signal (see Sec. 2.1.4);Our strategy for dealing with drag is twofold: to partially compensate the effect of air drag (by drag free control, with FEEP thrusters) and partially reject it (by balancing the coupled suspension of the GG test bodies).
For drag compensation the requirements are:
![]() (2.37)
(2.37)
in the
x,y transverse plane and along the z spin/symmetry axis of the spacecraft respectively. Mini FEEP thrusters are capable to provide the required maximum thrust of about 65.18 m N with this resolution. FEEP thrusters and their control electronics for GG are presented in Sec. 4.2; the proposed thruster configuration is given in Sec. 5.5 and the drag-free controller is presented in Sec. 6.1.15 with results from numerical simulations. Compensation is required at the orbital frequency (the frequency of the signal vector before modulation), and since the thrusters spin with the spacecraft, they must act at their spin frequency (relative to the center of the Earth). A notch filter is therefore used (see Sec. 6.1.15) which appears to work very well; it shows no difficulty in controlling non gravitational effects also at higher frequencies (i.e. twice the orbital frequency or the natural differential frequency of the test bodies). It is apparent that the control compensates for any non gravitational forces acting on the surface of the spacecraft at the frequencies of the notch filter. Note that, because of firing at the spin frequency (or close to it) and of being fixed on the spacecraft outer surface, thruster firing will induce undesired vibration noise (at the modulation frequency of the signal); however, such noise is very effectively attenuated by the mechanical suspensions of the PGB, as shown by the transfer function in Fig. 2.6.The requirement on drag compensation along the z axis (by a factor 1/150) is dictated by the necessity of reducing non gravitational effects along the spin/symmetry axis, which would displace the centers of mass of the bodies, hence giving rise to tidal perturbations from the Earth; these effects are presented in the next Section where the above requirement is also derived.
As for balancing the test bodies (see Sec. 2.1.4) in order to reject common mode forces and leave only a much smaller residual differential effect competing with the signal, the requirement is:
![]() (2.38)
(2.38)
With the GGG payload prototype we have achieved so far a balancing level better than this requirement by a factor of 2 (see Chap. 3). Given that the largest force to be balanced in space is @ 2.7× 10-8 of the local gravity acceleration to be balanced on Earth, this requirement can be regarded as well doable. Indeed, a more stringent one can be posed, either to improve the sensitivity or in the case that it would become necessary to release the requirement (2.37) on drag compensation. Although at some point the experiment will become limited by thermal noise (see Sec. 2.2.7), it is very important to have good margins on the balancing requirement while using FEEP technology, which is innovative and is subject to further testing. Even more important is the fact of being able to test the balancing on the ground instead of relying on calculations only.
There will be air drag disturbances at the natural frequencies of the test bodies (particularly the one for differential oscillations w dm) due to air density variations (known air granularities) over distance scales of about a thousand km. The corresponding density is smaller than average atmospheric density, typically by at least a factor of 10. For these disturbances to resonate with the natural frequencies of the system, they must act at a frequency whose distance from the resonant frequency is within the width of the gaussian, namely w dm/Q . With Q @ 20000 for the test bodies of the GG experiment (Q measurements reported in Sec. 2.1.5) there is no way that air granularities over a thousand km can act on the spacecraft so precisely close to the natural differential frequency of the test bodies.
The amplitude of the displacements caused on the GG suspended bodies by the air drag (maximum) acceleration (2.36) can be easily computed once the natural frequencies of oscillation are known. With the current GG set-up the values of the relevant natural frequencies - and periods- (checked with the numerical simulations reported in Sec. 6.1.10) are:
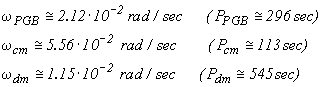 (2.39)
(2.39)
for - respectively- the PGB, the test bodies in common mode and the test bodies in differential mode. The PGB is displaced because of drag (relative to the spacecraft) by:

This is the amplitude of the largest displacement that the PGB will ever be subject to; it is therefore apparent that, in spite of weighing several tens of kg (with the test bodies, capacitors etc… inside), the PGB can very well be suspended by means of very weak springs like the one shown in Fig. 2.5.
Once at the level of the test bodies, air drag effect has been reduced by the drag free control, hence, the amplitude of the largest displacement of the test bodies (in common mode) is:
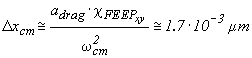 (2.40)
(2.40)
involving the helical springs and flat gimbals shown in Figs. 2.2. and 2.3. This value allows us to quantify the requirement to be fulfilled in the mechanical balancing of the read-out capacitance bridge. According to inequality (2.15) the capacitance plates of the read out (see Fig. 2.11) must be positioned halfway between the outer surface of the inner test cylinder and the inner surface of the outer one to within:
a-b À 1.86 m m (2.41)
(if the half-width of the gap is
5 mm), i.e. the requirement for balancing of the bridge is:![]() (2.42)
(2.42)
With inch-worms actuators adjusting distances with the resolution of about
1m m is no problem at all.Having partially compensated and partially rejected the drag, the residual differential displacement it causes on the centers of mass of the test bodies one with respect to the other is:
 (2.43)
(2.43)
This competes with the signal given by Eq. (2.2). However, it is at about
90° from the signal (the largest drag component is along track while the signal is radial, as shown in Fig. 1.1), and we have verified in the numerical simulation that this very important information is not lost by the controller during drag compensation (see Sec. 6.15). Thus, after demodulation of the signal the EP vector and the drag perturbation vector will be as shown in Fig. 2.21, which allows us to distinguish the residual drag even if it is a factor of 2 larger than the signal. A gain of a factor 2 in distinguishing signals well separated in phase is commonly accepted by experimentalists, and this is taken into account in the GG error budget given in Tables 2.1 and 2.2.2.2.2 Earth Tidal Perturbations
The GG mission goal is to detect, or to place a stricter upper limit on, a very small differential displacement between test bodies of different composition which cannot be accounted for by
classical, known laws of physics. However, tides are a well known classical phenomenon producing differential displacements between bodies orbiting around the Earth whose centers of mass do not perfectly coincide, because the gravitational field of the Earth is not uniform.Let us first consider tides in the transverse
x,y plane. We know that once rotating the GG test bodies will self-center to within about 1 Angstrom (see Sec. 2.1.5). More importantly, it has been stressed that the relative position vectorThe center of mass of the GG test bodies will not be exactly centered on one another along the spin/symmetry z axis either. And if the centers of mass of the test bodies are not at the same height along the spin axis (z axis) there is a tidal relative acceleration in the transverse plane (plane of signal) due to the Earth unless the spin axis is exactly perpendicular to the orbit plane. Since the spin axis (along which a displacement gives rise to a tidal acceleration component in the transverse plane) is fixed in the inertial space, the tidal effect is detected by the sensors at their spinning angular frequency w s; the amplitude of the signal goes from maximum, to zero, to a negative maximum, in half orbit period of the satellite around the Earth. With its spin axis at a non-zero angle h n from the orbit normal, the GG spacecraft has "seasons" like the Earth around the Sun. This tidal effect is maximum at the "solstices" and zero at the "equinoxes" of the GG satellite; the "summer" solstice and the "winter" solstice differ in that the tidal signal changes sign between the two (i.e., the signal changes sign at twice the orbital frequency) (see Fig. 2.22). However, with the sensors spinning much faster, the two effects differ from one another by a fraction of about 1/10000 and it is therefore better that this particular tidal effect be below the expected EP signal.
The offset h n of the GG spin axis from the orbit normal is expected not to exceed 1° (see Sec. 5.1). The corresponding Earth tidal acceleration in the x,y at an orbiting altitude h is given by:
![]() (2.44)
(2.44)
This tidal signal is detected by the capacitance read-out and it is used in the initial calibration phase to drive the piezo actuators (as described in Fig. 2.14) in order to reduce the axial miscentering D z: once the tidal acceleration signal has become too small to be detected it will also be too small to perturb the EP experiment. The idea of using the tidal signal to drive an active control of the centers of mass of the test bodies was initially put forward by P. Worden for STEP. However, there is a component of solar radiation pressure along the z axis which will cause a corresponding inertial acceleration of the test bodies along z (similarly to what happens in the transverse plane). This effect is in principle common mode, but we make the conservative assumption that 1/100 of it will remain as a residual differential effect . It means that solar radiation will keep displacing the center of mass of the test bodies along z. The effect is close to zero near the equinoxes of the Earth's orbit around the Sun and close to its maximum near the solstices of the Earth. If we now require that FEEP drag free control be operational also along the z axis (by only a factor 1/150), the amplitude of the largest D z displacement that solar radiation can give rise to, turns out to be of about 2 Angstrom. With this value the tidal perturbing acceleration (2.44) is well below the signal and no active vertical centering of the centers of mass of the test bodies is necessary to be driven by the tidal signal. In fact, a vertical miscentring up to 5 Angstrom would still be acceptable to avoid recentering.
Figure 2.22 Simple scheme of Earth tidal forces on two test bodies which rotate around the same axis but whose centers of mass are displaced along it. The figure shows how the component of the tidal force towards the Earth changes phase by 180° every half orbital period of the satellite around the Earth. Only this component does produce a differential displacement of the centers of mass which can be recorded by the spinning capacitors. It is apparent that a differential force due to a violation of the Equivalence Principle would not change sign every 1/2 orbit and would also not go to zero with the separation distance D z.
2.2.3 Radiometer Effects and Thermal RequirementsThe radiometer effect is well known in gravitational experiments as a dangerous "experiment killer". It is caused by the differential pressure of the residual gas on the cylindrical test bodies, and therefore one way of reducing it is by reducing the residual pressure. This choice has led scientists to lower the temperature to very low values, until almost all gases freeze out and only an extremely low pressure is left. In GG, since the signal of interest is not along the symmetry axis of the test bodies, but in the perpendicular plane, the major contribution by the radiometer effect is zero for symmetry reasons even at room temperature. We have examined all contributions caused by this effect in GG, and concluded that they do not affect the EP experiment at the current target sensitivity of 1 part in 1017, as it is summarized below (see Comandi et al., 1998 for details)
The perturbing acceleration known under the name of "radiometer effect" is:
![]() (2.45)
(2.45)
with p, r and T the pressure, density and temperature of the body with a gradient along the x direction. This happens in conditions such as the space ones in which the mean free path of the gas molecules is much larger than the linear dimension of the vessel. Consider the concentric hollow test cylinders of the GG experiment, with the symmetry axes in the z direction and the expected EP violation signal in the transverse x,y plane. A radiometer acceleration in the x,y plane would compete directly with the signal. Consider one of the hollow cylinders with its inner and outer surfaces at temperatures differing by D T, perfect azimuthal symmetry and zero temperature gradient along z. For pure symmetry reasons there is no radiometer acceleration normal to the axis of the cylinder. If the two cylinders are placed one inside the other and their axes are perfectly aligned there is no differential force between the two in the x,y plane due to the radiometer effect. An imperfect centering of the cylinders would break this symmetry, but we have checked that it would require a very large temperature difference between the test cylinders to become relevant. We take T=300 K and p=1.1× 10-7 N/m2
(corresponding to a residual density of 2× 10-16 g/cm3 ; maximum value close to solar maximum). Due to the fast spin and with well known insulation techniques azimuth temperature asymmetries of the test bodies are negligible; the resulting radiometer effect (due to the resulting break of symmetry) is also negligible.The only relevant requirement comes from the radiometer effect along the spin/symmetry axes of the test cylinders. Although the signal is in the transverse plane, we have just seen in the previous Section that the vertical misalignment D z between the centers of mass of the test bodies should not exceed a few Angstrom in order not to give rise to a tidal effect competing with the signal and requiring recentering. If we compute the radiometer effect along the z axis we get the following inequality:
![]() (2.46)
(2.46)
which must be fulfilled by temperature gradients along z, So and Si being the cross sections, in the x,y transverse plane of the outer and inner cylinder respectively, and kz the elastic constant of the suspensions along z. Temperature gradients along z (over the height of the test bodies) must not exceed a few degrees.
The radiation pressure effect along z leads to a similar requirement on D Tz : if the two faces of a test cylinder have different temperatures they will emit differently, and this will result in a net force along the symmetry axis of the cylinder. This effect will be different for the two bodies, hence resulting in a differential acceleration (and a differential displacement) along the z direction. The inequality to be fulfilled by the axial temperature gradients because of this effect is:
![]() (2.47)
(2.47)
(c the speed of light, s the Boltzmann constant, e the emissivity - about 0.03 for gold coating- S the cross section of the body in the x,y transverse plane). It is more stringent for the outer body, due to the larger S, and leads again to a few degrees.
Yet another requirement on temperature gradients along z , this time along the coupling arms of the test bodies (see Fig. 2.1), is due to the fact that temperature gradients change the length of the arms, whereby impairing the balancing of the test bodies. It is enough to choose the material for manufacturing the arms with a coefficient of thermal expansion of 10-5 /K ; then, if temperature gradients along each arm do not exceed 1 K the balancing is not perturbed.
In this low equatorial orbit the GG satellite spends about 1/3 of its time in the shadow of the Earth and the rest in sunlight, thermal equilibrium temperatures in the two cases differing by several tens of degree. While azimuth temperature variations are inexistent because of the fast spin, temperature gradients between the illuminated and the dark side of the satellite when exposed to radiation can in principle be very large. These gradients can be essentially eliminated inside a rapidly spinning spacecraft if it is properly insulated. Insulation and vacuum serve also the purpose of reducing the rate of temperature variation with time. For the temperature stability in time inside the PGB laboratory at the level of the test bodies we require that:
![]() (2.48)
(2.48)
which, from thermal model simulations, turns out to be feasible by passive control only (see Sec. 4.4).
The temperature drift affects the stiffness of the suspensions, hence the balancing of the test bodies because the springs will not respond exactly the same to the same temperature changes. We require that the relative change in stiffness with temperature be of 1/4000 per degree of temperature; experience with gravimeter springs for the measurement of Earth tides has shown that it can be done much better (Melchior et al. 1979). If 1/100 of the stiffness variation is differential (which is reasonable because the test bodies springs are manufactured to high precision, and can be tested in the laboratory), then there is a time interval of 20 days before exceeding the required common mode rejection level (given by 2.38) whereby the test bodies need to be rebalanced.
If the test bodies expand uniformly (in azimuth), the relative position of their centers of mass does not change; hence the signal will not change as long as the capacitance bridge remains balanced. However, the capacitance sensors will change their relative position in between the test bodies to such an extent that the bridge may no longer be balanced. If this happens, a common mode signal may become dominant over the expected differential signal. With the requirement (2.42) on bridge balancing this will take about 15 days. However, once the materials for the test bodies have been selected (Be and Cu in the current baseline) and the bodies have been manufactured, thermal tests can be done so that the mounting arms of the capacitance can be manufactured using a material whose coefficient of thermal expansion partially compensates for the bridge unbalance caused by the thermal expansion of the test bodies. In this way the allowed time-span before mechanical rebalancing of the bridge would become longer than 2 weeks. Non uniform thermal expansion of the test bodies is small and gives a DC effect.
In summary, current temperature requirements (0.2 K/day stability in time at test masses level; 1 K axial gradient over the test bodies and the coupling arms) appear to be doable with passive thermal insulation techniques (see Secs. 4.3 and 5.4); they allow 20 days of data taking before rebalancing of the test bodies and at least 15 days (more if some more care is taken in the manufacture of the sensor plates arms) before rebalancing the read-out capacitance bridge.
2.2.4 Electrostatic and Magnetic Effects
Electrostatic effects are known to be a major challenge in all gravitational experiments due the @ 1040 ratio in strength between the two interactions. The GG orbit (low and equatorial) is below the Van Allen belts and minimizes charged particles impact. However, the major advantage of the GG experiment is that, with conductive mechanical suspensions there are no free floating masses and therefore no electrostatic charges will be able to build up inside the spacecraft. Care will be taken that all currents flow in shielded cables. Potential differences between the test masses can be avoided by coating them with a thin layer of the same conductive material. Small residual potential differences (known as patch effects) may be present with slow time variations. In GG they would give essentially DC effects. Such potential differences can only be detected from their mechanical effects. This can be done with the GGG ground prototype; if a known potential V is applied to a capacitance plate facing the test body the resulting force is proportional to V2. Therefore, by changing sign to the voltage any deviation from a parabolic dependence (hence any bias A V) can be measured.
A comparison with STEP makes it apparent how serious charging problems can be. In STEP as studied by ESA at Phase A level for the M3 competition (with a target in EP testing of 1 part in 1017 like GG), a 2-cm thick tungsten shield (weighing @ 130 kg) was considered as baseline in order to have a time span of a few days available before discharging was needed again (Blaser et al., 1996 Mission Summary and Sec. 3.6.1). In the previous Phase A Study of STEP carried out by ESA for the M2 competition in collaboration with NASA (same target in EP testing) the problem had already been recognized as a serious one, although the baseline solution was a different one: it was decided to add a radiation sensor on board so as to be able to discard the contaminated data (Blaset et al., 1993 Sec. 3.4.4). In addition, it must be noted that in STEP charged particles affect the EP experiment also by asymmetrical momentum transfer along the sensitive axis of the test bodies, especially because their masses are small (a few hundred grams) (Blaser et al., 1993, Sec. 3.4.3). It is therefore a very good feature of GG to be essentially unaffected by Van Allen belt effects and electrostatic charging.
Magnetic disturbances are of two types: interactions of magnetized or magnetizable materials between themselves and interactions between these materials and the Earth's magnetic field. The effects appear at g s-g ã (g ã p 7.29Ñ 10-5rad/s the rotation angular velocity of the Earth, g ã ¸ g s), at 2(g s-g ã ), hence essentially at the spin frequency and twice it, and as DC. All these effects have been estimated in worst case assumptions (see Nobili et al., 1998a for details on all various terms).
The most dangerous perturbation is due to the interaction between the magnetic moment (due to residual ferromagnetic impurities) of one test body and the magnetization induced on the other by the magnetic field of the Earth. The resulting perturbing force, at frequency w s and therefore competing with the signal is:
![]() (2.49)
(2.49)
with Bã the magnetic field of the Earth, h mp 118 the angle between north geographic and north magnetic pole, x 1 and V1 the magnetic susceptibility and volume of test mass 1, m 2 the magnetic moment of test mass 2, r the mutual distance. The requirement on the magnetic moment of the Be test mass is to be smaller than about 7.5× 10-8 Am2 . From experimental data reported in textbooks we find that the magnetic moment of a cube of magnet of 0.1 mm size (which would be a large magnetic impurity) is about 5× 10-7 Am2 , so with care in avoiding large magnetic impurities our requirement can be met.
At the spin/signal frequency there is also the perturbation due to the interaction of the magnetic moment of one test body with the magnetic field of the Earth:
![]() (2.50)
(2.50)
but the constraints it poses on residual magnetic moments are much easier to fulfill. Magnetic effects close to twice the spin frequency, and those DC have been evaluated and found out not to be a matter of concern.
Taking into account that these are worst case estimates, it can be safely concluded that the GG experiment does not need magnetic shielding. In STEP magnetic shielding is needed because of the use of SQUID sensors and its is provided by superconducting lead shields (Blaser et al., 1993 Sec.3.4.6).
By comparison, it is worth considering the problem of magnetic perturbations in the Eö t-Wash EP torsion balance experiment (Su et al., 1994), where the magnetic field of the Earth near the balance was reduced by a total factor of 105 (partly with W -metal shielding, partly with Helmholtz coils). This seems to contradict our previous conclusion, especially if one considers that they have reached a sensitivity R = 10-12 while the GG target is R = 10-17. Indeed, it is not so and we can easily understand why. The first important fact to bear in mind is that, despite its higher target sensitivity the GG expected force signal is p 2.5 times larger than it is in Eö t-Wash, because of the bigger EP signal in space and the larger mass of the test bodies. In GG there are two test bodies of 10 kg each while in the Eö t-Wash torsion balance there are 4 masses of 10 grams each; the force signals are p 8.4. 10-16 N and p 3.4. 10-16 N respectively. Note that the force, not the acceleration, is relevant when dealing with non gravitational perturbations. Secondly, since the Eö t-Wash experiment is a torsion balance experiment it is sensitive to torques, hence also to the magnetic torque generated by the interaction of the magnetic field of the Earth with magnetic moments of the test bodies (due to residual ferromagnetic impurities). Indeed, it turns out that the magnetic moment of the tray on which the test bodies are positioned gives an even larger perturbation than the test masses themselves. For this torque to be smaller than that due to an EP violation it must be:
![]() (2.51)
(2.51)
where p 0.03 m is the length of the arm. It must therefore be W tray < 2· 10-13Am2 (having used Bã = 5· 10-5 T). From measurement of the torsion angle in absence of any shielding or coils the Eö t-Wash group finds that the residual magnetic moment of the tray (made of Al) is about 2.4· 10-8 Am2 (Su et al., 1994; Su 1992), thus making a reduction of Bã by 105 crucial for the success of the experiment. This is achieved by means of a 3-layer W -metal shielding for a factor 3,600 and of Helmholtz coils for a factor 28. As for the Eö t-Wash test masses, the measured value of the residual magnetic moment is p 4· 10-10 Am2 while the requirement imposed by the magnetic torque is about 7· 10-9 Am2; with a factor 105 of reduction of the magnetic field of the Earth made necessary by the tray, this effect is no problem. The magnetic dampers, used to kill the swing and wobble modes so that the motor can provide a smooth rotation, will also benefit of the reduction of the magnetic field. In GG we have symmetric and concentric masses and the signal is a force, not a torque, thus we have nothing like the magnetic torque (2.51); we do not have any motor or magnetic dampers either.
2.2.5 Coupling to Higher Mass Moments of the Test Bodies
The GG test bodies have non zero quadrupole and higher mass moments. These are different for the two bodies and will therefore interact differently with the monopole moment of the Earth. The result is a (classical, i.e. Newtonian) differential acceleration which experimentally is absolutely undistinguishable from an EP violation signal: the source mass is the same, the mass moment which produces the effect is the same (the monopole), so the resulting frequency and phase are also the same. For this reason, this is the single most dangerous perturbation whose value has to be absolutely below the expected signal to make EP test unambiguous. The perturbing acceleration caused by the Earth mass interacting with the quadrupole moment of a test body orbiting at an altitude h is:
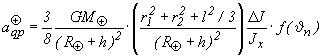 (2.52)
(2.52)
with r1, r2 and l the inner radius, outer radius and height of the body, h the altitude of the satellite, D J/Jx5 (Jz2 Jx)/Jx5 b the fractional difference in the principal moments of inertia and q n<18 the angle between the spin axis and the orbit normal (f(q n) p 1 for small h n). In the GG current design (taking into account that coupling to a given monopole source with the quadrupole moments of the test bodies is in phase, and therefore the relative effect is the difference of the two, the resulting effect is given in the error budget Tables 2.1 and 2.2 and it is below the signal by two orders of magnitude. Coupling to mass moments higher than the quadrupole gives much smaller disturbances because the Earth is far away (large value of Rã +h).
Nearby mass anomalies A m in the mass distribution of the satellite will also produce a similar coupling. But the big difference is that these effects are DC; an advantage of the entire laboratory spinning with the test bodies which unfortunately is not there in the GGG ground test. So values larger than the signal are acceptable, and we can avoid putting tight constraints on symmetry of the mass distribution (by construction), which might be expensive requirements to meet. We find that 100 grams unbalance on the outer shell where such anomalies are more likely to be (at about 40 cm distance), gives a quadrupole effect at most 30 times larger than the signal, which is not a problem because it is a constant DC effect . We have been worried about the expansion and contraction of the outer shell (and compensation masses) induced by eclipses (Sec. 2.1.2). Even though the signature of an eclipse induced signal can in principle be recognized (the frequency is the orbital one, but eclipse lasts only about on third of the orbital period) eclipse induced effects would still be a concern. In fact the gravitational effect of such an oscillation turns out to be negligible because the test bodies are well centered on the symmetry axis of the cylinder where the effect of a pulsating cylindrical surface would be exactly zero. Hence, the dominant effect remains the one of a mass anomaly by construction estimated above.
2.2.6 Requirements and Disturbances from Whirl Control
The stabilization of whirl motions as outlined in Sec. 2.1.5 and numerically simulated in Chap. 6 gives a requirement on the measurement of the spin rate of the spacecraft:
![]() (2.53)
(2.53)
to be met by the Earth Elevation Sensors of the spacecraft (see Sec. 5.5). Currently available sensors, e.g. from Officine Galileo, are usually mounted on higher altitude spinning spacecraft. They would therefore need to be modified for the lower orbit of GG (the angle between the two small infrared telescopes needs to be increased) but the requirement is not a challenging one. Note that, although the spin rate needs to be measured to this level, it does not matter how much it is precisely. Also the precise direction of the spin axis in space does not matter because the active dampers act, by geometrical construction, in the plane perpendicular to the spin axis; where precisely this axis is in space is not needed. This comes from the fact that the EP differential signal would be measured, by construction, in the same plane perpendicular to the spin axis. However, the analysis of the output data of the Earth sensors will provide also the direction of the spin axis.
The whirl control needs the small capacitance sensors to be able to detect relative displacements of 0.01 m m , particularly for the test masses. This is the sensitivity which, after applying filters at the spin frequency and at the whirl/natural frequency, allows us reducing the whirl radii to values of a few Angstrom. The sensitivity required for these small capacitance sensors has been demonstrated in the laboratory during the development of the GGG prototype (see Chap. 3).
Disturbances induced by the active control of the test masses themselves need not to be taken into account because the growth times of their whirl motions are so slow (due to the high mechanical quality of the suspensions; Q=19000 measured) that a convenient strategy is to first damp the whirls with forces much larger than the minimum required (so as to damp them quicker) and then start data taking. The planned integration time of about 1 week can be carried without controlling the whirls of the test bodies. The whirl motion of the PGB needs to be damped all the time because its suspensions have a lower mechanical quality (smaller Q). There are perturbations on the relative position due to the controlling forces if they are not perfectly opposite to the whirl velocity but have also a radial component, because of a phase error. However, perturbations on the PGB are common mode for the test bodies, hence only their residual differential fraction (after common mode rejection) gives a differential effect and competes with the signal: with c CMR = 1/100000 disturbances from the control forces of the PGB are totally negligible even with a very large phase error.
2.2.7 Thermal Noise and Error Budget
Test masses will have their own mechanical thermal noise, resulting in a perturbing acceleration on each test mass:
 (2.54)
(2.54)
where KB is the Boltzmann constant, m =10 kg is the mass of each test body, w dm the natural oscillation frequency of the test bodies in differential mode, Q the quality factor of the mechanically suspended bodies and tint the integration time.
It is a well known fact that in supercritical rotation suspensions are deformed (and dissipate energy) at their spinning frequency, not at their natural frequency. This applies to GG as well (Crandall and Nobili, 1997). In this case the relevant Q is that of the suspension springs of the test masses at 2 Hz, for which our best measured value is 19000 (see Sec. 2.1.5). Having the natural frequency w dm rather than the one in common mode in (2.54) is correct: the two values are not close (see 2.39) and Q is high, hence the bandwidth of noise is so small that there is no significant contribution from thermal noise in common mode to the thermal noise in differential mode where the effect of an EP violation would appear. It is also worth noticing the dependence of thermal noise acceleration on (T/m)1/2 , which shows how bigger masses can compensate for the higher temperature in a room temperature rather than cryogenic experiment as it is GG at present.
Table 2.1 gives the GG error budget listing the major disturbances with the signature of their effects (frequency and phase), since this is very important in establishing how they contribute to the total budget. This Table assumes launch at the beginning of 2002 and mission operation for 7 months after launch, the first month being devoted to initial set-up and calibration phase. Being close to the solar maximum air drag is the main disturbance; moreover, the maximum value of drag along the orbit is used for a conservative evaluation. It is partially compensated and partially rejected; the common mode rejection factor of 1/100000 assumed here is a very realistic one, since it has already been tested on the GGG prototype (see Chap. 3). Also the Q value, which is relevant for thermal noise, derives from experimental measurements (see Sec 2.1.5). The signal is about a factor of 2 above the total error.
In Table 2.2 the error budget refers to operating the mission close to solar minimum, in the fall of 2004; however, the maximum value of drag along the orbit is used. Drag is clearly less relevant, also because we have assumed an improvement in common mode rejection by a factor of 5, which experience with the ground prototype shows it can be reached. Thermal noise has become the limitation; we have also assumed to be able to improve the Q by a factor 50, to a value 100000. Such a possibility can be tested in the laboratory; the target value appears to be reachable but it is not as easy as improving the common mode rejection. The signal is now about a factor 5 larger than the error.
In conclusion, EP testing with the GG experiment - at room temperature and with an almost passive satellite- to 1 part in 1017 is feasible. Doing better than this requires to substantially lower the temperature flying a cryogenic version of GG. In this case the GG rapid axial rotation gives two important advantages: (i) the very high centrifugal force at the periphery of the spacecraft dominates the motion of the refrigerating (movable) material and largely reduces, by symmetry, its well known disturbances on the experiment; (ii) the spin/symmetry axis provides an ideal symmetrical direction along which evaporation can take place without disturbing the experiment. None of these advantageous features holds for the current, cryogenic STEP experiment.
Table 2.1 GG Error Budget for EP testing to 10-17 (SI Units): close to solar maximum (launch beginning of 2002); maximum drag value along the orbit assumed; Q as measured; c CMR tested in GGG.
Acceleration (transverse plane) DUE TO: |
Formula |
Frequency (inertial frame) (Hz) |
Frequency (detected by spinning sensors) (Hz) |
Phase |
Differential acceleration(m/sec2 ) |
Differential displacement(m) |
| EP SIGNAL |
|
w.r.t. Earth |
Test body to center of Earth |
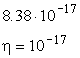 h=520 Km |
|
|
Air Drag |
|
|
|
~ along track |
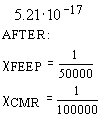 |
|
Solar radiation pressure |
|
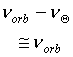 |
|
test body to center of Earth component |
same
|
|
Infrared radiation from Earth |
|
|
|
test body to center of Earth |
same
|
|
Earth coupling to test bodies quadrupole moments |
|
|
|
test body to center of Earth |
|
|
Mechanical thermal noise |
|
|
|
Random |
|
|
Total Error Budget |
|
Table 2.2 GG Error Budget for EP Testing to 10-17 (SI Units): close to solar minimum (launch 2004); maximum drag value along the orbit assumed; improvement in Q and c CMR required.
Acceleration (transverse plane) DUE TO: |
Formula |
Frequency (inertial frame) (Hz) |
Frequency (detected by spinning sensors) (Hz) |
Phase |
Differential acceleration(m/sec2) |
Differential displacement(m) |
| EP SIGNAL |
|
w.r.t. Earth |
Test body to center of Earth |
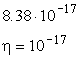 h=520 Km |
|
|
Air Drag |
|
|
|
~ along track |
|
|
Solar radiation pressure |
|
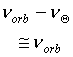 |
|
test body to center of Earth component |
same
|
|
Infrared radiation from Earth |
|
|
|
test body to center of Earth |
same
|
|
Earth coupling to test bodies quadrupole moments |
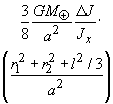 |
|
|
test body to center of Earth |
|
|
Mechanical thermal noise |
|
|
|
Random |
|
|
Total Error Budget |
|