Various adjustments can be performed for the rotating differential accelerometer to operate as it is designed to. An inclination of the (rotating) coupling arm, about its midpoint, by a non-zero (constant) angle from the vertical, gives rise to a constant relative displacement of the test cylinders fixed in the rotating frame. It is therefore detected by the (rotating) read-out as a constant offset from zero (in X and Y), which provides the driving signal for this adjustment. In order to reduce this offset the position of the top suspension (the one of the outer test cylinder; see Fig. 2) can be adjusted so as to be as much as possible in line with the other two suspensions at the center and the bottom. This is the coarsest adjustment. Then, on the coupling arm, close to (just below) the central suspension, are mounted two small masses (5 g each) that can be displaced across the arm's axis in the X and Y directions in order to reduce the corresponding offsets, and therefore the inclination of the arm. For yet a finer adjustment there are two additional smaller masses (0.5 g each), also movable in X and Y.

However, a constant offset in the X and Y measurements of the relative displacements between the centers of mass of the test cylinders as performed by the rotating capacitance bridges may also be due to the bridge capacitances being out of balance at zero mechanical displacement; which would require the variable capacitances in each bridge to be adjusted, and no change in the inclination of the coupling arm. In order to separate the two effects, and operate the right adjustment, we perform these measurements by spinning the rotor at a frequency first below and then above the natural one for differential oscillations of the test cylinders. If the offsets are due to the inclination of the coupling arm, i.e. to the test cylinders not being suspended along the same axis, it is known that that they should decrease when spinning above the natural frequency (see e.g. Den Hartog, 1985; Crandall, 1995; Genta, 1993). Once a non-zero inclination of the coupling arm has been ruled out, we can proceed to reduce the offsets of the measurements by adjusting the variable capacitances. A few iterations of this procedure may be necessary.

Around the lower half of the coupling arm is mounted a small solid ring (see section in Fig. 2), movable in the vertical direction. A change in its vertical position, by changing the mass distribution of the beam balance, will change the natural period of the differential oscillations (see discussion on Eq. (1)). Being symmetrical around the arm, the position of the ring does not affect its inclination. From an operational viewpoint, this is the easiest way to change and adjust the differential period of the test cylinders.

In the conceptual design of the differential accelerometer it is very important that the suspension shaft (the tube enclosing the coupling arm, held by a shaft turning inside ball bearings, to which rotation from the motor is transmitted by means of O-rings on pulleys; see Fig. 2) be aligned with the local vertical. In the case of a non-zero inclination of the suspension tube from the local verticaldue to the shaft not being mounted perfectly vertical in the laboratory reference framethere will be a non-zero lateral deformation of the central suspension which suspends the beam balance (see Fig. 2), and a consequent relative displacement of the test cylinders. The displacement is fixed in the laboratory (non-rotating) frame along the direction identified by the misalignment of the shaft and is modulated by the rotating capacitance bridges at their spin frequency. The X and Y bridge measurements are transformed into the X_nr and Y_nr relative displacements in the non-rotating frame (see Section 4) where the coordinates of the fixed displacement indicate the direction of the deflection of the suspension shaft. They provide the driving signal for this adjustment, which is performed by means of three vertical micrometric screws (at 120° from one another) which control the inclination of the top plane of the frame around the shaft (see Fig. 3), hence also its verticality. The micrometric screws are differential and allow both coarse and fine adjustments. A still finer adjustment of the verticality of the suspension shaft is performed by means of three (vertical) piezoelectric actuators (PTZs, also at 120° from one another) perpendicular to the horizontal plane at the top of the rotor, on which it rests. They allow finer adjustments of the verticality of the shaft than micrometric screws can do, and moreover they can be remotely controlled from outside the vacuum chamber. In addition, if the central suspension which carries the weight of the whole system is not centered on the rotation axis, the centrifugal force will compress the same PZTs at the frequency of spin. Their three signals are acquired by means of a National Instruments card and allow us to adjust the position of the central suspension on the rotation axis by means of three micrometric screws mounted horizontally around it, so as to reduce the PZTs signals as much as possible.

As the systems spins the suspensions are deformed at the spin frequency and the relevant loss factors (inverse of quality factor Q) are those of the mechanical suspensions at the spin frequency. The effects of such dissipation are unstable forward whirl motions whose frequencies are close to the natural frequencies of the system. The destabilizing forces which generate the whirl motions are equal to the passive spring forces divided by the Q. The magnitude of the forces is the same in the stationary and in the rotating frame; only their frequencies change. The forces required to achieve neutral equilibrium are equal and opposite to the destabilizing forces. They never exceed the passive spring forces as long as Q is larger than 1. For large Qs the destabilizing forces, as well as the active ones required for stabilization, are much smaller than the passive spring forces. This also means that the instabilities to be damped grow very slowly. The negative Q which determines the growth of the whirl motions is equal (with the opposite sign) to the Q of the suspensions at the frequency of spin (Genta, 1993; Crandall and Nobili, 1997; Nobili et al., 1999).

In the rotating accelerometer of Fig. 2 whirl motions can be stabilized either passively (by providing sufficient non-rotating damping) or actively, by means of small capacitance sensors/actuators which must be controlled to counteract the destabilizing forces which generate the whirl motions. In the GG space experiment, where there are no non-rotating parts (no motor is needed once the spacecraft is set in rotation at the nominal spin rate) whirl motions can only be actively controlled (Nobili et al., 1999; "GALILEO GALILEI" (GG), Phase A Report, 1998, Chapter 6). In the differential accelerometer of Fig. 2 a passive, non-rotating damper, made of a very light disk with little radial blades immersed in oil for vacuum, is mounted on the inner test cylinder, below its suspension from the coupling arm (it is shown in yellow and gray in Fig. 2, but only its base is visible in Fig. 3). It stabilizes the whirl motion at the natural differential frequency of the test cylinders, as measurements show (see Section 5). The passive damper is also equipped with a mechanism mounted in the vacuum chamber outside the accelerometer itself (it is clearly visible in Fig. 3 in front of the accelerometer) that can be activated from outside the chamber in order to run the system with or without damping of whirl motion and to measure (when off) the whirl growth rate, which provides the Q of the system at the spin frequency (Section 5). We can also use this on/off mechanism during testing of the active damper. The active damper (not shown in Figs. 2 and 3) is made by eight small capacitance plates facing the outer test cylinder (one layer of four sensors and one of four actuators, the two pairs of sensors forming the two halves of two capacitance bridges in the two coordinates of the horizontal plane). The electronics of these bridges is essentially the same as that of the bridges of the main sensors (Section 4, Fig. 9) except for the fact that here smaller capacitances and less good sensitivity are needed. The signals from these two bridges drive the four (high) voltages for the four actuators.

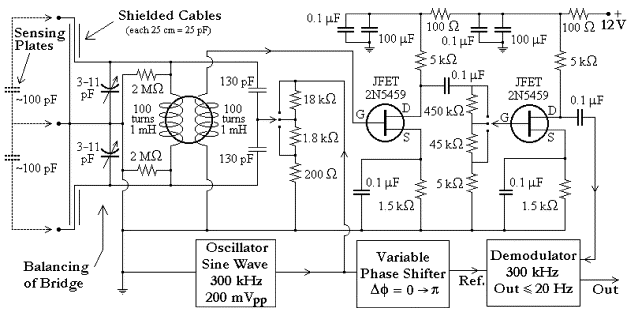
Fig. 9. The capacitance bridge sensor circuits used in the accelerometer of Figs. 2 and 3 for the read-out of the relative displacements of the test cylinders.