An experiment which aims at testing the equivalence principle must be capable to detect
tiny relative displacements of the test masses with respect to one another. However,
spurious relative motions would appear, because of gravity gradients, were the centres of
mass of the test bodies not accurately centred on one another. This is why the test masses
must be concentric, as they are in STEP. In GG their cylindrical shape is not only a
construction advantage; it is clearly dictated by the symmetry of the one axis rotation.
The crucial question is: how, and to what accuracy, is mass centering obtained? The answer
comes from a careful exploitation of weightlessness, which makes the mechanical system
(spacecraft, PGB and test masses) a rotor in supercritical rotation with the spin
frequency ![]() much larger than the
natural oscillation frequency
much larger than the
natural oscillation frequency ![]() of the suspended test masses (and the PGB laboratory as well). Since the end
of last century such rotors are known to have an equilibrium position very close to the
rotation axis, which is pivotal in reducing the otherwise destructive effects of
centrifugal forces in high-speed machines such as turbines, centrifuges and ultra-vacuum
pumps (see Whitley (1984) for a review). In
simple terms, the rotor tends to spin around its centre of mass, i.e. it behaves more like
a free rotor rather than a constrained one. If the centre of mass of the suspended body is
located, by construction, at a distance
of the suspended test masses (and the PGB laboratory as well). Since the end
of last century such rotors are known to have an equilibrium position very close to the
rotation axis, which is pivotal in reducing the otherwise destructive effects of
centrifugal forces in high-speed machines such as turbines, centrifuges and ultra-vacuum
pumps (see Whitley (1984) for a review). In
simple terms, the rotor tends to spin around its centre of mass, i.e. it behaves more like
a free rotor rather than a constrained one. If the centre of mass of the suspended body is
located, by construction, at a distance ![]() from the rotation axis, equilibrium is established on the opposite side
of
from the rotation axis, equilibrium is established on the opposite side
of ![]() with respect to the rotation
axis, where the centrifugal force due to rotation and the restoring elastic force of the
suspension equal each other. It can be shown that this happens at a distance from the spin
axis smaller than the original unbalance
with respect to the rotation
axis, where the centrifugal force due to rotation and the restoring elastic force of the
suspension equal each other. It can be shown that this happens at a distance from the spin
axis smaller than the original unbalance ![]() by a factor
by a factor ![]() (see, e.g., Ch. 6 of Den Hartog, 1985).
Thus, at equilibrium, the distance
(see, e.g., Ch. 6 of Den Hartog, 1985).
Thus, at equilibrium, the distance ![]() of each suspended test mass inside the GG satellite from the spin
axis - and therefore from one another - is:
of each suspended test mass inside the GG satellite from the spin
axis - and therefore from one another - is:
![]()
Since the pioneer work of Gustaf De Laval about a century ago this relationship has been
widely demonstrated in both theoretical and experimental work on high speed rotors. It
shows that space offers an important advantage, because in absence of weight the natural
frequencies of suspended bodies can be very low, about ![]() smaller that the spin frequency in this case. For an original
unbalance
smaller that the spin frequency in this case. For an original
unbalance ![]() this means that the
equilibrium position is only
this means that the
equilibrium position is only ![]() away
from the spin axis. It is important to stress that this equilibrium position slightly
displaced from the rotation axis is fixed in the rotating frame of the spacecraft while
the signal is modulated at the frequency of spin. Possible imperfections on the surfaces
of the bodies would also give a DC effect. The actual direction of the miscentering in the
rotating system depends only upon the location of the unbalance and is of no importance
for the experiment. Perturbations such as air drag and solar radiation pressure acting on
the external surface of the spacecraft produce a nongravitational acceleration of its
centre of mass. In the reference frame of the spacecraft the bodies will therefore be
subject to inertial forces in the opposite direction, which will move the masses to new
displaced positions of equilibrium (along the direction of the perturbation) where the
perturbation is balanced by the restoring force of the spring. It is worth noticing that,
because of the supercritical state of rotation, the displaced body will always spin around
its own axis, which means that no centrifugal force due to the spin will result because of
this displacement. The only centrifugal forces due to the spin come from the
away
from the spin axis. It is important to stress that this equilibrium position slightly
displaced from the rotation axis is fixed in the rotating frame of the spacecraft while
the signal is modulated at the frequency of spin. Possible imperfections on the surfaces
of the bodies would also give a DC effect. The actual direction of the miscentering in the
rotating system depends only upon the location of the unbalance and is of no importance
for the experiment. Perturbations such as air drag and solar radiation pressure acting on
the external surface of the spacecraft produce a nongravitational acceleration of its
centre of mass. In the reference frame of the spacecraft the bodies will therefore be
subject to inertial forces in the opposite direction, which will move the masses to new
displaced positions of equilibrium (along the direction of the perturbation) where the
perturbation is balanced by the restoring force of the spring. It is worth noticing that,
because of the supercritical state of rotation, the displaced body will always spin around
its own axis, which means that no centrifugal force due to the spin will result because of
this displacement. The only centrifugal forces due to the spin come from the ![]() miscentering given by Eq. 3 and are balanced by the restoring force of the
suspension springs.
miscentering given by Eq. 3 and are balanced by the restoring force of the
suspension springs.
It is however well known that any rotating system operating in the supercritical regime is unstable - owing to its internal damping - unless an adequate "non-rotating damping" is applied to it, that is damping caused by friction of the non rotating - or slowly rotating - parts of the bearings (on which the spinning shaft is mounted) against their supports. See Bramanti et al. (1996), Nobili et al. (1996) for an analysis of the various types of friction. Since the spacecraft as a whole is rotating, there is no way of obtaining the required non-rotating damping except by increasing the complexity of the system with the introduction of a fixed or slowly rotating portion of it. A simpler solution is to place in between the various masses active elements able to simulate the behaviour of a non-rotating damper. In the language of automotive active suspension technology the device can be defined as a "skyhook damper" since it acts as a damper which in a way follows an inertial reference frame. In Section 3.1 we show the main properties of supercritical rotation and the rôle of internal and non-rotating damping in a simplified mathematical model of two masses connected with springs; then report the results of a finite element numerical simulation of the system in the 3-chamber setup of Fig. 1 , giving all the unstable whirling modes of the system and showing how they are damped (Section 3.2 ). The electrostatic damper is discussed in Section 3.3 .
Unlike GG, the STEP experiment has been based on the fact that its
attitude be actively maintained fixed with respect to inertial space as well as drag-free
(in angle) to a level compatible with the requirement on orbital drag-free, which turns
out to be a very demanding requirement. In this way, with a considerable effort in
accurate active control, an EP violation signal from the Earth would appear at the
satellite orbital frequency (![]() ).
However, since the signal frequency is the frequency of orbital motion around the Earth it
is bound to be also the frequency of a number of dangerous perturbing effects (e.g from
the South Atlantic Anomaly and from the on board Helium used to make the experiment
cryogenic). More recently it has been proposed that the STEP spacecraft be spinning too,
but only slightly faster than its orbital revolution around the Earth. The benefits of
fast satellite spin could not be incorporated either in the first proposed rotating
experiment (Chapman & Hanson, 1970). In
that experiment centrifugal forces remain a major limitation because the test bodies are
constrained to move along one diameter of the rotating platform, and it is well known that
any such rotating system is always strongly unstable above the critical speed (Ch. 6, p.
228 of Den Hartog, 1985).
).
However, since the signal frequency is the frequency of orbital motion around the Earth it
is bound to be also the frequency of a number of dangerous perturbing effects (e.g from
the South Atlantic Anomaly and from the on board Helium used to make the experiment
cryogenic). More recently it has been proposed that the STEP spacecraft be spinning too,
but only slightly faster than its orbital revolution around the Earth. The benefits of
fast satellite spin could not be incorporated either in the first proposed rotating
experiment (Chapman & Hanson, 1970). In
that experiment centrifugal forces remain a major limitation because the test bodies are
constrained to move along one diameter of the rotating platform, and it is well known that
any such rotating system is always strongly unstable above the critical speed (Ch. 6, p.
228 of Den Hartog, 1985).
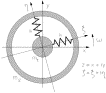
Fig. 5. A mathematical model of two axially symmetric bodies of masses
and
coupled by springs of stiffness k.
and
are the inertial and the rotating plane respectively. z and
are the complex variables in the two planes.
Let us first study the system in the simplified model of two
axisymmetrical rigid bodies of masses ![]() and
and ![]() , length
, length ![]() , moments of
inertia
, moments of
inertia ![]() and
and ![]() with respect to their
symmetry (polar) axis and
with respect to their
symmetry (polar) axis and ![]() ,
, ![]() with
respect to any transversal axis x, y. The bodies are coupled by two
identical springs, each of radial stiffness k as shown in Fig. 5 . By introducing the complex coordinates
with
respect to any transversal axis x, y. The bodies are coupled by two
identical springs, each of radial stiffness k as shown in Fig. 5 . By introducing the complex coordinates ![]() and
and ![]() , where
, where ![]() and
and ![]() are the rotation angles
around the y and x axes (the minus sign allows to simplify the metrical form
of the equations), the equation of motion for the lateral dynamics of the system is
(Section 4.6 of Genta, 1993):
are the rotation angles
around the y and x axes (the minus sign allows to simplify the metrical form
of the equations), the equation of motion for the lateral dynamics of the system is
(Section 4.6 of Genta, 1993):
![]()
where
![]()
is the vector of the generalized coordinates of the system (subscripts 1 and 2 distinguish
the two bodies) and ![]() ,
, ![]() ,
, ![]() are known as the mass,
gyroscopic and stiffness matrices:
are known as the mass,
gyroscopic and stiffness matrices:
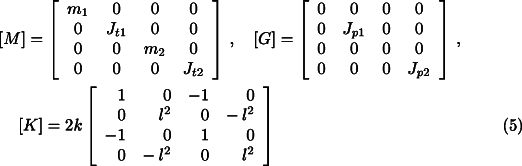
Because of possible construction errors each body will have the centre of gravity located
a distance ![]() away from its rotation
axis, and the symmetry axis tilted by an angle
away from its rotation
axis, and the symmetry axis tilted by an angle ![]() with respect to its rotation axis. These unbalances
will result in the forcing terms at the right hand side of the equation of motion (Eq. 4 ) which contain the vector
with respect to its rotation axis. These unbalances
will result in the forcing terms at the right hand side of the equation of motion (Eq. 4 ) which contain the vector ![]()
![]()
where ![]() defines the direction of the
vector
defines the direction of the
vector ![]() in the rotating frame
and
in the rotating frame
and ![]() is the phase
angle of the couple due to the unbalance. In the general case of the Jeffcott rotor (Jeffcott, 1919) the system is subject to
nonconservative forces (damping forces) which can be of two kinds: either of fixed
direction in the inertial frame (non-rotating damping) or of fixed direction in the
rotating frame (rotating damping). The latter occurs in the parts of the system which spin
at speed
is the phase
angle of the couple due to the unbalance. In the general case of the Jeffcott rotor (Jeffcott, 1919) the system is subject to
nonconservative forces (damping forces) which can be of two kinds: either of fixed
direction in the inertial frame (non-rotating damping) or of fixed direction in the
rotating frame (rotating damping). The latter occurs in the parts of the system which spin
at speed ![]() (e.g. the springs), while
the former is linked with the nonrotating parts of the machine. They are usually expressed
as matrices
(e.g. the springs), while
the former is linked with the nonrotating parts of the machine. They are usually expressed
as matrices ![]() and
and ![]() respectively,
with
respectively,
with ![]() the total
damping matrix of the system. In the case of GG the entire system is spinning and
therefore there is no non-rotating damping, i.e.
the total
damping matrix of the system. In the case of GG the entire system is spinning and
therefore there is no non-rotating damping, i.e. ![]() and
and ![]() . The matrix
. The matrix ![]() is given by:
is given by:
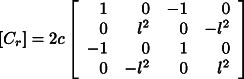
where c is the damping coefficient. For internal hysteretic damping the value of c,
for the translational modes, can be approximated as ![]() , with Q the quality factor and
, with Q the quality factor and ![]() .
.
Because of symmetry Eq. 4 can be split into two different sets of uncoupled equations, one for the translational modes
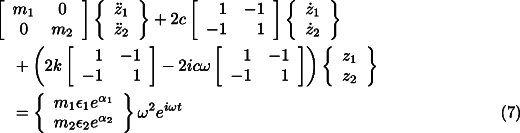
and one for the rotational modes
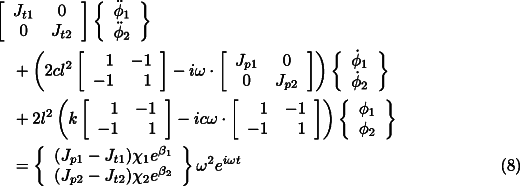
Let us consider the equation for the translational dynamics of the system (Eq. 7 ). Assuming a solution of the type ![]() for the free whirling, the
characteristic equation of the homogeneous system is
for the free whirling, the
characteristic equation of the homogeneous system is
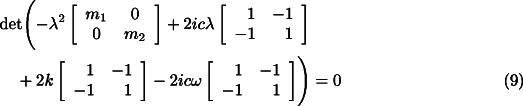
whose solutions (i.e. the complex frequencies of the system) are 0 and the solutions of
the equation:
![]()
which is the characteristic equation of a Jeffcott rotor with mass ![]() in the absence of
non-rotating damping. It is well known that this device is unstable at all speeds
exceeding the critical speed (see, e.g., 4.8.3 of Genta,
1993)
in the absence of
non-rotating damping. It is well known that this device is unstable at all speeds
exceeding the critical speed (see, e.g., 4.8.3 of Genta,
1993)

Thus, without non-rotating damping operation in supercritical regime (i.e. above the
critical speed) is not possible because the rotor is necessarily unstable. From a more
physical point of view, the springs - because of their internal dissipation - will
necessarily transfer the spin angular momentum of each body to their rotational motion
around one another, giving rise, in the inertial reference frame, to a circular forward
motion of increasing amplitude of each axial end of the rotation axis of each body around
the equilibrium position. There is a cylindrical whirl if the two ends move in phase and a
conical (also called precessional) one if they move ![]() out of phase. The natural position of equilibrium with the two
axes very accurately aligned still exists but whirling motions around it necessarily grow
in time, inevitably bringing the system to instability. It is worth stressing that if the
suspension springs are very tiny, with very low stiffness k and relatively high Q
values, the timescales of these instabilities are large, as numerical simulations confirm
(Section 3.2 ). This is very important in devising an
efficient active damper.
out of phase. The natural position of equilibrium with the two
axes very accurately aligned still exists but whirling motions around it necessarily grow
in time, inevitably bringing the system to instability. It is worth stressing that if the
suspension springs are very tiny, with very low stiffness k and relatively high Q
values, the timescales of these instabilities are large, as numerical simulations confirm
(Section 3.2 ). This is very important in devising an
efficient active damper.
Non-rotating damping can be simulated by an active device which exerts
on the mass ![]() a force
a force
![]()
where ![]() is the
overall gain of the device and
is the
overall gain of the device and ![]() is the complex displacement measured in the rotating reference frame
is the complex displacement measured in the rotating reference frame ![]()
![]() as shown in Fig. 5 . The device exerts a force of the same intensity
and direction but opposite sign on the mass
as shown in Fig. 5 . The device exerts a force of the same intensity
and direction but opposite sign on the mass ![]() . In the inertial reference frame
. In the inertial reference frame ![]() the equation of motion of the system is now given
by Eq. 4 by adding the term
the equation of motion of the system is now given
by Eq. 4 by adding the term
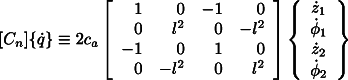
to its left hand side. Assuming again a solution of the type ![]() for the free whirling, the
characteristic equation of the homogeneous system for translational motions is
for the free whirling, the
characteristic equation of the homogeneous system for translational motions is
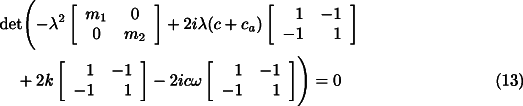
whose solutions are 0 and the solutions of the equation:
![]()
which is the characteristic equation of a Jeffcott rotor with mass ![]() , non-rotating damping
, non-rotating damping ![]() and rotating damping c.
It is well known that this device is stable at all speeds below the maximum value
and rotating damping c.
It is well known that this device is stable at all speeds below the maximum value ![]()
![]()
It follows that rotation at supercritical speed ![]() which were to ensure very good centering (i.e.
which were to ensure very good centering (i.e. ![]() ) as well as stability necessarily requires
) as well as stability necessarily requires ![]() . The case of the test masses
in the GG satellite is a very favourable one because the tiny suspension springs have very
low internal damping c due to the very low stiffness k and relatively high Q.
Hence a small amount of active damping
. The case of the test masses
in the GG satellite is a very favourable one because the tiny suspension springs have very
low internal damping c due to the very low stiffness k and relatively high Q.
Hence a small amount of active damping ![]() is sufficient to guarantee stability even at a spin
frequency
is sufficient to guarantee stability even at a spin
frequency ![]() much larger than the
critical frequency
much larger than the
critical frequency ![]() .
Thus, the active dampers are neither required to provide large forces nor to operate with
small response times, since the unstable modes of the rotor are characterized by low
frequencies (see Section 3.2 ). The nice fact about
supercritical rotation is that the equilibrium position, with the axes closely aligned, is
a physical property of the system and unstable rotational motions around this equilibrium
position take place very slowly. This makes relatively easy centering to the position of
equilibrium by means of active damping, clearly much easier than it would be in absence of
such a naturally provided position of equilibrium. In Section
3.3 we present an electrostatic damper that appears to be suitable for our purposes.
Here we wish to stress that in the rotating reference frame (to which the electrostatic
plates of the damper are attached as shown in Fig. 2 )
it must supply a force with components:
.
Thus, the active dampers are neither required to provide large forces nor to operate with
small response times, since the unstable modes of the rotor are characterized by low
frequencies (see Section 3.2 ). The nice fact about
supercritical rotation is that the equilibrium position, with the axes closely aligned, is
a physical property of the system and unstable rotational motions around this equilibrium
position take place very slowly. This makes relatively easy centering to the position of
equilibrium by means of active damping, clearly much easier than it would be in absence of
such a naturally provided position of equilibrium. In Section
3.3 we present an electrostatic damper that appears to be suitable for our purposes.
Here we wish to stress that in the rotating reference frame (to which the electrostatic
plates of the damper are attached as shown in Fig. 2 )
it must supply a force with components:
![]()
Thus, since the effect produced by the damper must be at the frequency of the whirling
motions, the unstable ones being at the (slow) natural frequency of oscillation, the
damper must actuate at the spin frequency minus the natural one, which is different from
the frequency of an EP violation. For the electrostatic plates to be able to recover and
damp the slow velocity of whirl while spinning much faster, the control software must be
able to subtract away their own velocity of spin, and this requires that either star
trackers or Earth elevation sensors provide a reference signal synchronized with the spin.
(For a detailed discussion on unstable whirl motions and active rotating damping in space
see Bramanti et al., 1996; GALILEO GALILEI, 1997; Nobili et al., 1996).

Fig. 6. Sketch of the FEM (Finite Element Method) model of GG. The figure shows the final FEM model used to analyse the rotordynamics of the active controlled system with DYNROT. The beam elements have been drawn on the left side of the picture: the white parts correspond to zero mass beams with structural stiffness. The nodes are shown on the right side of the sketch, each node corresponding to two translational and two rotational degrees of freedom which describe the lateral dynamics. In order to provide an understandable overview each node has been located on the corresponding beam element, instead of on the rotation axis of the satellite, as it actually is. Since each active damper has been connected to the central rod there are shorter beam elements near the gimbals and two nodes very close to each other.
Fig. 7. Schematic representation of the various components of one experimental chamber placed next to one another in order to show the different kind of connections between them (springs, gimbals and electrostatic dampers). The outer and the inner test mass are respectively connected by spring elements (continuous line) to the pair of movable supports. Gimbals join the movable supports to the central rod, while the electrostatic dampers act between the test masses and the central rod (dotted line).
A more realistic model was built using the finite element
rotordynamics code DYNROT, developed over the years at the Department of Mechanics of
"Politecnico di Torino". The model, which includes the satellite body, the PGB
laboratory and three pairs of test masses, is shown in Fig.
1 where the numbers 1-8 distinguish the various components of the system for later
reference. The test masses are connected to the PGB by very low stiffness springs and
movable supports with elastic gimbals at their midpoints as shown in Fig. 2 . We first compute the whirling modes of the system
assuming that no active dampers are present. The model consists of 36 beam elements and 20
spring elements (see Fig. 6 , Fig. 7 ). A number of beam elements which is larger than
the minimum necessary to model the 8 cylindrical bodies and the central rod with movable
supports has been used in order to allow us to define the location of the attachment
points of the springs. The stiffness of the beam elements is orders of magnitude larger
than that of the springs, so that they behave as rigid bodies in the whole frequency range
of interest. Beam elements have been chosen instead of concentrated mass elements in order
to use the ability of the code to compute directly the inertial properties from the
geometrical parameters. Once the model was built, the number of degrees of freedom was
reduced from 98 complex degrees of freedom, related to the displacements and rotations of
all 49 nodes, to 16 through Guyan reduction (see, e.g., Section 2.8 of Genta, 1993). The minimum number of degrees of freedom
necessary to define rigid-body motion was chosen, thus ensuring that no deflection of the
beam elements can occur. The inertial properties of the rigid bodies are listed in Table 1 , where the numbers 1-8 refer to the various parts
of the system as shown in Fig. 1 . The ratio ![]() is also listed. The masses of
the central rod and of the movable supports have been neglected. The code was run using
the same stiffness of
is also listed. The masses of
the central rod and of the movable supports have been neglected. The code was run using
the same stiffness of ![]() , both longitudinal and transversal, for all the springs (2 for each body) and
the same torsional constant
, both longitudinal and transversal, for all the springs (2 for each body) and
the same torsional constant ![]() , for all the elastic gimbals (2 for each pair of test masses). This value can
be obtained if the diameter of the wires in the gimbals is about
, for all the elastic gimbals (2 for each pair of test masses). This value can
be obtained if the diameter of the wires in the gimbals is about ![]() and their length from
and their length from ![]() to
to ![]() . The stiffness of the springs is relevant in response to forces in
common mode while the gimbals enter into play when a pair of coupled test masses is
subject to a differential force, resulting in an equivalent transverse stiffness
. The stiffness of the springs is relevant in response to forces in
common mode while the gimbals enter into play when a pair of coupled test masses is
subject to a differential force, resulting in an equivalent transverse stiffness ![]() (l is the length of
the rod from the gimbal to the spring, that is the arm; l is between
(l is the length of
the rod from the gimbal to the spring, that is the arm; l is between ![]() and
and ![]() in the 3-chamber model of Fig. 1 ).
The resulting equivalent transverse stiffness are therefore not exactly the same, but they
are all smaller than the
in the 3-chamber model of Fig. 1 ).
The resulting equivalent transverse stiffness are therefore not exactly the same, but they
are all smaller than the ![]() stiffness of the springs. In the code the system is simplified in that either
the springs or the gimbals respond, depending on whether the motion is in common mode
(both masses together) or in differential mode (one mass with respect to the other)
respectively. While it is true that the gimbals do not affect common mode motions, the
springs play a rôle also in differential motions. However, they respond to differential
deformations with a lower elastic constant (the bending constant) than they do in the case
of transversal common mode deformations. How much smaller is computed by Den Hartog
(Appendix, p. 429 of Den Hartog, 1985), for a
beam, and the numerical factor is 4. In laboratory tests with helicoidal springs we have
measured a factor 3. Each pair of suspended test bodies will therefore have a lower
natural frequency for oscillations in differential mode and a higher one for those in
common mode:
stiffness of the springs. In the code the system is simplified in that either
the springs or the gimbals respond, depending on whether the motion is in common mode
(both masses together) or in differential mode (one mass with respect to the other)
respectively. While it is true that the gimbals do not affect common mode motions, the
springs play a rôle also in differential motions. However, they respond to differential
deformations with a lower elastic constant (the bending constant) than they do in the case
of transversal common mode deformations. How much smaller is computed by Den Hartog
(Appendix, p. 429 of Den Hartog, 1985), for a
beam, and the numerical factor is 4. In laboratory tests with helicoidal springs we have
measured a factor 3. Each pair of suspended test bodies will therefore have a lower
natural frequency for oscillations in differential mode and a higher one for those in
common mode: ![]() and
and ![]() (where
(where ![]() is the equivalent transverse
stiffness and k the stiffness of each spring;
is the equivalent transverse
stiffness and k the stiffness of each spring; ![]() because there are two springs for each mass and m because
the reduced mass between the test mass m and the rest of the spacecraft is
essentially m). A factor about 2 between these frequencies is reasonable to obtain,
and this is the situation simulated with the DYNROT code.
because there are two springs for each mass and m because
the reduced mass between the test mass m and the rest of the spacecraft is
essentially m). A factor about 2 between these frequencies is reasonable to obtain,
and this is the situation simulated with the DYNROT code.
Table 1. Inertial properties of the rigid bodies (as numbered in Fig. 1) which constitute the FEM model
Fig. 8. Mode shapes of GG satellite. The mode shapes found by the DYNROT FEM code can be divided into three types: the first includes 7 cylindrical modes forward and backward, the second 7 backward mainly conical modes and the third 8 conical forward modes. A sample of each set including the
and
forward modes and the
backward mode is shown by giving the position of the axis of rotation (continuous line) and the location of the nodes (the "
" symbols). The x-
is a coordinate along the spacecraft axis (in cm); the y-
is an adimensional normalized coordinate (the mode automatically scales all the modes to the maximum value).
The frequencies of free whirling are computed for the spacecraft spin
rate ![]() . Apart from the zero
frequency modes, we find (in
. Apart from the zero
frequency modes, we find (in ![]() ): a
set of 7 backward mainly conical whirling modes of frequencies
): a
set of 7 backward mainly conical whirling modes of frequencies ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ; a set of 7 cylindrical modes, forward and
backward of frequencies
; a set of 7 cylindrical modes, forward and
backward of frequencies ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ; a set of 8
conical forward whirling modes of frequencies
; a set of 8
conical forward whirling modes of frequencies ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() close to the spin
frequency. A graphical representation for some of the computed modes is given in Fig. 8 . With the introduction of some internal damping of
the springs which suspend the test masses (e.g.
close to the spin
frequency. A graphical representation for some of the computed modes is given in Fig. 8 . With the introduction of some internal damping of
the springs which suspend the test masses (e.g. ![]() it is found that only the forward cylindrical modes
become unstable, and the e-folding times are a few
it is found that only the forward cylindrical modes
become unstable, and the e-folding times are a few ![]() (all other modes are naturally damped). As expected, instabilities
are there but they build up slowly. As for the PGB laboratory the timescales for
instability are shorter because, although the mass is bigger than that of the test bodies,
the quality factor
(all other modes are naturally damped). As expected, instabilities
are there but they build up slowly. As for the PGB laboratory the timescales for
instability are shorter because, although the mass is bigger than that of the test bodies,
the quality factor ![]() of its springs is smaller. Note that all modes with eigenfrequencies close to the
spin/signal frequency are conical (i.e. angular precessions), not cylindrical modes, which
means that they do not affect the centre of mass of the bodies whose relative displacement
is the observable in this experiment. Moreover, it is well known and the simulations
confirm it, that they are naturally damped, i.e they are not unstable. We can conclude
that there is no interference between these modes and the signal. As for the frequencies
of the 7 cylindrical modes listed above (both forward and backward, the forward ones being
those which become unstable in the presence of a nonzero internal damping of the springs)
we note that they are the eigenfrequencies of the suspended bodies (two for each pair of
test masses plus one for the PGB laboratory) as they have been computed in the numerical
simulation of the 3-chamber system. As a matter of fact, since we study the mechanical
system as a whole these are the natural frequencies of the system; however, due to
the weakness of the springs, they can be still recognized as due to the various suspended
masses. In order to avoid mutual mechanical influences between the three pairs of masses
it is sufficient that their frequencies be separated by a few times their bandwidths. In
this simulation in which all the springs have a stiffness of
of its springs is smaller. Note that all modes with eigenfrequencies close to the
spin/signal frequency are conical (i.e. angular precessions), not cylindrical modes, which
means that they do not affect the centre of mass of the bodies whose relative displacement
is the observable in this experiment. Moreover, it is well known and the simulations
confirm it, that they are naturally damped, i.e they are not unstable. We can conclude
that there is no interference between these modes and the signal. As for the frequencies
of the 7 cylindrical modes listed above (both forward and backward, the forward ones being
those which become unstable in the presence of a nonzero internal damping of the springs)
we note that they are the eigenfrequencies of the suspended bodies (two for each pair of
test masses plus one for the PGB laboratory) as they have been computed in the numerical
simulation of the 3-chamber system. As a matter of fact, since we study the mechanical
system as a whole these are the natural frequencies of the system; however, due to
the weakness of the springs, they can be still recognized as due to the various suspended
masses. In order to avoid mutual mechanical influences between the three pairs of masses
it is sufficient that their frequencies be separated by a few times their bandwidths. In
this simulation in which all the springs have a stiffness of ![]() and all the gimbals have a
torsional constant of
and all the gimbals have a
torsional constant of ![]() the DYNROT code provides: a frequency of about
the DYNROT code provides: a frequency of about ![]() to be associated with the oscillations of
the PGB and corresponding to an elastic constant
to be associated with the oscillations of
the PGB and corresponding to an elastic constant ![]() ; three frequencies between
; three frequencies between ![]() and
and ![]() to be associated with the differential modes; three higher
frequencies between
to be associated with the differential modes; three higher
frequencies between ![]() and
and ![]() to be associated with the common modes. From
now on we use
to be associated with the common modes. From
now on we use ![]() for the common mode
and
for the common mode
and ![]() for the differential mode,
noticing that there is enough liberty in the choice of the springs and gimbals to actually
obtain these values. The corresponding elastic constants are:
for the differential mode,
noticing that there is enough liberty in the choice of the springs and gimbals to actually
obtain these values. The corresponding elastic constants are: ![]() , for the response to forces
in differential mode and
, for the response to forces
in differential mode and ![]() for the response of each mass to forces in common mode. The fact of having a
good separation between the eigenfrequencies in common mode and those in differential mode
(the latter being smaller) is very useful because in this way displacements in response to
perturbations in common mode (air drag) are reduced while those in differential mode (EP
violation) are increased.
for the response of each mass to forces in common mode. The fact of having a
good separation between the eigenfrequencies in common mode and those in differential mode
(the latter being smaller) is very useful because in this way displacements in response to
perturbations in common mode (air drag) are reduced while those in differential mode (EP
violation) are increased.
At this point we insert into the model a set of ideal active dampers
providing the force (Eq. 16 ). In doing so we also
refine the model by increasing the number of elements to 82 (48 beam elements, 20 spring
elements and 14 active dampers). The model includes 61 nodes and the number of degrees of
freedom is reduced from 122 complex degrees to 16 through Guyan reduction. We assume a
gain of ![]() for all
the 12 elements damping the test masses. It is found that all unstable modes become stable
and the timescales for damping are of 1 to 10 hours. For details on the physics of
unstable whirl motions and their active control with rotating electrostatic dampers see Bramanti et al. (1996), GALILEO GALILEI (1997), Nobili et al. (1996).
for all
the 12 elements damping the test masses. It is found that all unstable modes become stable
and the timescales for damping are of 1 to 10 hours. For details on the physics of
unstable whirl motions and their active control with rotating electrostatic dampers see Bramanti et al. (1996), GALILEO GALILEI (1997), Nobili et al. (1996).

Fig. 9. Electrostatic damping of whirling motions. The circular instability motions of the rotation axis of the inner shaft, which have the natural (low) frequency of the suspended masses
, can be actively damped by means of the electrostatic force obtained by applying a voltage pulse V of short duration (for example for about one fourth of the spin period, i.e. about
) to each plate rotating at the (rapid) spin frequency
when it is passing through the position
before the point of its nearest approach to the inner shaft. This happens, for each plate, at a frequency which is equal to the spin frequency
minus the natural frequency
.
The force acting between the two elements of the electrostatic damper (Fig. 9 ) for an assumed voltage V is (in MKS):
![]()
with S the surface of the actuator and x the gap between the equipotential
surfaces of the damper. For small displacements and tensions the force can be linearized
around a constant voltage ![]() and reference gap
and reference gap ![]() for a superimposed control voltage
for a superimposed control voltage ![]() yielding
yielding
![]()
The second term on the right hand side describes the behaviour of a spring element with
negative stiffness, and this must be softer than the mechanical springs: those linking PGB
to the spacecraft body and those connecting each test masses to the central rod. The
actuator is driven by a power amplifier modulated by the controller output signal. It
provides the control voltage ![]() to the capacitive load constituted by the pair of electrostatic actuators.
The resulting transfer function between the controller output signal
to the capacitive load constituted by the pair of electrostatic actuators.
The resulting transfer function between the controller output signal ![]() and the control voltage
and the control voltage ![]() is (the variable s
indicates a Laplace transform with respect to time)
is (the variable s
indicates a Laplace transform with respect to time)
![]()
with ![]() the stationary
gain and
the stationary
gain and ![]() the power
amplifier bandwidth. The transfer function between the displacement from the reference
position of the rotor and the sensor output signal
the power
amplifier bandwidth. The transfer function between the displacement from the reference
position of the rotor and the sensor output signal ![]() , including the conditioning circuitry, is
, including the conditioning circuitry, is
![]()
with ![]() the stationary
gain and
the stationary
gain and ![]() the sensor
bandwidth. In order to behave as required by Eq. 16 the
controller must supply the output signals
the sensor
bandwidth. In order to behave as required by Eq. 16 the
controller must supply the output signals ![]() and
and ![]() for the plates acting respectively in
for the plates acting respectively in ![]() and
and ![]() directions in accordance with the sensor outputs
directions in accordance with the sensor outputs ![]() and
and ![]() in the same directions. The
input-output relationships of the controller can be written in the form
in the same directions. The
input-output relationships of the controller can be written in the form
![]()
with ![]() and
and ![]() the stationary gains,
and
the stationary gains,
and ![]() the time
constant of the causal pole of the derivative term. By comparing Eq. 16 , Eq. 21 it
follows that the stationary gains of the controller must satisfy the relationships
the time
constant of the causal pole of the derivative term. By comparing Eq. 16 , Eq. 21 it
follows that the stationary gains of the controller must satisfy the relationships
![]()
It is easy to verify that a gain ![]() can be obtained with
can be obtained with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . The negative stiffness of
the electrostatic damper due to
. The negative stiffness of
the electrostatic damper due to ![]() is
is ![]() ,
lower than the stiffness of the springs.
,
lower than the stiffness of the springs.
We have shown the feasibility of an electrostatic active damper with the characteristics required to ensure stability. The approximations introduced, particularly as far as the simulation of the electric circuit is concerned, are quite rough. Also, the dynamics of the sensors, controllers and power amplifiers has been neglected. However, the results are essentially correct because the frequencies at which the system works are quite low, orders of magnitude smaller than the characteristic frequencies of the electronic subsystems.
As for the thermal noise of the electrostatic active damper we have:
![]()
where ![]() is the
equivalent resistance of the electrostatic damper of capacity
is the
equivalent resistance of the electrostatic damper of capacity ![]() and electric quality
factor
and electric quality
factor ![]() operated at
frequency
operated at
frequency ![]() . Then,
. Then,
![]()
Since the force exerted by the damper is ![]() (
(![]() the potential difference) the perturbing force corresponding to the noise is
the potential difference) the perturbing force corresponding to the noise is ![]()
![]() . Dividing by the mass
. Dividing by the mass ![]() of the test body we get the
perturbing acceleration:
of the test body we get the
perturbing acceleration:
![]()
A comparison with the mechanical thermal noise (Section
6.2 ) shows that with a reasonable value of the electric quality factor ![]() , and
, and ![]() the contribution of each
electrostatic damper to the thermal noise is negligible and it remains so even considering
that the damping of each test body involves 8 capacitance plates. This result could be
guessed from the fact that the force to be provided by each plate is very small. In point
of fact we plan to confirm this result with experimental tests of the electrostatic
damping system in the framework of a ground experimental test of the equivalence principle
based, as GG, on supercritical rotation and mechanical suspension of concentric test
cylinders.
the contribution of each
electrostatic damper to the thermal noise is negligible and it remains so even considering
that the damping of each test body involves 8 capacitance plates. This result could be
guessed from the fact that the force to be provided by each plate is very small. In point
of fact we plan to confirm this result with experimental tests of the electrostatic
damping system in the framework of a ground experimental test of the equivalence principle
based, as GG, on supercritical rotation and mechanical suspension of concentric test
cylinders.
Let us now estimate the amount of shot noise to be expected:
![]()
where ![]() and
and ![]() is the potential difference
due to the quantized current
is the potential difference
due to the quantized current ![]() . With a capacity
. With a capacity ![]() for
each electrostatic damper we get:
for
each electrostatic damper we get:
![]()
If ![]() (but usually is
much smaller) the shot noise is about 5 times bigger than the thermal noise given by Eq. 24 , which we have just seen to be negligible with
respect to the mechanical thermal noise of the test masses.
(but usually is
much smaller) the shot noise is about 5 times bigger than the thermal noise given by Eq. 24 , which we have just seen to be negligible with
respect to the mechanical thermal noise of the test masses.
Copyright © 1998 Elsevier Science B.V., Amsterdam. All Rights Reserved.
![]()
![]()
![]()
(Anna Nobili- nobili@dm.unipi.it)