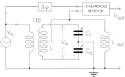
The displacements of the test masses are detected with a pair of capacitors in a circuit which is essentially an LC bridge, formed by two resonant coupled oscillators, as shown in Fig. 14 . The plates of the capacitors are sections of cylinders concentric to the test bodies (Fig. 15 ) and are supported by the frame shown in Fig. 2 .
Fig. 14. Outline of the read-out circuit. The two variable capacitors
and
and the two halves of the inductor L form an LC bridge whose output is proportional to the difference between the two capacitances.
Fig. 15. Each capacitor of the read-out system (see also Fig. 16 ) is formed by two surfaces, one for each of the two grounded masses, and one plate, to which a sinusoidal voltage is applied. Any differential displacement of the test masses with respect to the plates causes a loss of balance of the system and therefore an output signal.
Fig. 16. The surfaces of the capacitors before and after: a) a common mode displacement and b) a differential mode displacement.
A voltage signal 
of angular frequency 
is applied to the bridge in order to shift the signal of interest to a frequency band with
a 
noise as small as
possible. We consider 
. The circuit has the greatest sensitivity when 
and when also the output
circuit resonates at the same frequency 
. Since 
we must have 
. Since the system has a bad heat dissipation, the amplitude of the signal
should not exceed, say, 1 Volt in order to reduce power dissipation. We set 
with 
. The two capacitors of the
bridge and are shown in Fig. 15 . The signal is applied to the plates and the test
masses are electrically grounded. Let us call a and b the initial distances
from the plate to the inner and outer mass respectively, with 
. If a and b are small a
simplified analysis can be carried out assuming zero curvature parallel plates, and the
initial values of the capacity are then 
(where 
is the dielectric constant of vacuum). In the cylindrical geometry the
algebra is somewhat more complicated but with no relevant changes in the results. Any
displacement of the test masses will change 
into 
for
and 
for . Such a displacement is the
combination of a common mode and a differential mode displacement 
, 
(Fig. 16 ). Because of the values of the capacity change into
and therefore 
.
Similarly for we
have:
hence, 
. For the
general displacement the total change of capacitance will be given by:
which at resonance determines the output signal through the relation:
where 
is the
electrical quality factor of the output circuit. For instance, if 
, 
, 
and 
we get 
and 
, given the
requirement to be sensitive to an EP displacement with 
(Section 2.1 )
to a 
confidence level, i.e. 
. As for the thermal noise, laboratory tests
have yielded:
and therefore, since 
, the differential displacement 
due to thermal noise is:
This means that the measurement accuracy required by the experiment can be achieved with
an integration time of about 
.
Thus, it is ruled out for the GG experiment be limited by the performances of the
capacitance read out. Care should be taken in keeping parasitic capacitances small.
However, since they depend on the geometry of the system, the resulting perturbation will
be DC. It is therefore enough to make sure that their effect does not exceed the
sensitivity by several orders of magnitude. It must be stressed that the required accuracy
of 
refers to relative
displacements - at the spin frequency - of the centres of mass of the test bodies, not to
their surface irregularities. The latter will only give DC effects.
It is apparent from Eq. 48 that for
the read out to be sensitive to the displacement caused by a possible EP violation
of the
corresponding (differential) signal must be larger than the signal due to the largest
possible displacement in common mode. Namely:
where 
and the
maximum common mode displacement is due to air drag and amounts to 
. Hence, the system must be balanced
to 
, which
means 
Å. This level of balancing
can be achieved actively by means of inch-worm piezoelectric actuators (Fig. 17 ) acting on the mechanical support of each
capacitance plate to make their distance from the test masses as equal as possible.
Inch-worm actuators are made of a combination of piezoceramics (no magnets) and can
achieve relatively large displacements by a succession of very fine steps. Two inch-worms
are needed for each plate, as shown in Fig. 2 . The
driving signal for this active balancing is a constant voltage obtained by a proper
analysis of the 
signal. There is
no danger to cancel an EP violation signal by actually making a and b
different because the largest common mode effect - which is due to air drag - is variable
in time. In any case, a phase check is able to tell whether the signal is due to air drag
or EP violation. Inch-worms with 1 Å stepsize are commercially available.
Fig. 17. Scheme of the inch-worm. Lateral piezoelectric actuators alternately fasten and release the extremities of the inch-worm to the sides of its container while the inner part is made to expand and contract by means of the other piezoelectrics. In this way the inch-worm can move on a relatively long path in successive very small steps.
We now consider the electrostatic force which affects each test mass.
Let's take the inner test mass in the concentric initial configuration of Fig. 15 . As the mass moves by an amount x it is
subject to an average force 
given by:
This means that the electric forces simulate a spring with a negative constant 
which could in principle be used to increase the displacement produced by the signal and
to reduce the natural frequency of the test masses, which would in turn reduce the
integration time because of the smaller thermal noise effect (Section 6.2 ). However, since the coupled suspension of
the test masses with gimbals appears to give a rather low natural frequency this
possibility needs not to be exploited.
Although a more detailed analysis is needed we conclude that a
capacitance read out system can reach the required precision of 
(corresponding to a confidence level in the displacement due to
an EP violation with )
in a very short time and is therefore by far adequate to the task. It is also worth
stressing that ground tests of the capacitance read out system are possible, not only for
the sensitivity of the circuit, but also for the balancing and corresponding reduction of
the common mode displacements. We are working on a laboratory experiment with concentric,
cylindrical test masses in high speed supercritical rotation and a capacitance read out
like the one envisaged for GG. It would be a ground test of the main components of the
space experiment as well as, possibly, a valuable EP experiment in its own right.
Copyright © 1998 Elsevier Science B.V., Amsterdam. All Rights Reserved.
(Anna Nobili- nobili@dm.unipi.it)
