Consider a 2 dimensional harmonic oscillator made of two equal point masses, each of
mass m, coupled by a spring of stiffness k/2 (which corresponds to the
stiffness k for an equivalent spring connecting each mass to the centre of mass of
the system). The general solution 
(for each mass) is an elliptical orbit with
the centre (not the focus) in the common centre of mass of the bodies:
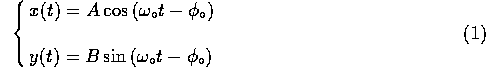
where the x,y coordinate axes are chosen to coincide with the symmetry
axes of the ellipse, 
is the natural frequency of the
oscillation, m/2 is the reduced mass of the system, 
is the phase, A and B
are the amplitudes along the symmetry axes. This general solution can be decomposed in
various ways into the sum of two simple harmonic motions. For instance, it can be written
as the sum of two circular oscillations, one forward and the other backward (for each
mass). They have the same frequency and phase but in general different ammplitudes:
where 
are the amplitudes of the forward and backward circular oscillations
respectively:
(Anna Nobili- nobili@dm.unipi.it)
