Consider a spacecraft of cylindrical symmetry whose symmetry axis is also the axis of
maximum moment of inertia. Inside the spacecraft is the PGB (Pico Gravity Box) laboratory,
also of cylindrical symmetry and with the axis of maximum moment of inertia coinciding
(within manufacture/mounting errors) with the symmetry axis of the spacecrfat. The PGB is
mechanically coupled to the spacecraft (along the sysmmetry axis) by means of mechanical
springs with low stiffness k in all directions. Let the spacecraft and PGB be
rigidly locked to one another during launch and until they have reached the nominal spin
angular velocity 
around the principal axis of inertia of the system. Let the cruise
phase, under the effect of a non-gravitational force 
(e.g. due to the atmospheric
drag), begin at time t=0, once the rigid lockers have been unlocked and the initial
transient phase has been completed. Since we refer here to the GG space experiment we
consider only the motion of the spacecraft/PGB system in the x,y plane
perpendicular to the spin axis, which is the plane of the expected signal; we know that
tilting torques are negligible, that differential rotations in azimuth can be dealt with
and that motions along the z-spin axis are sufficiently small (see ``GG
Pre Phase A Report'', ASI, September 1996)
In an inertial reference frame whose centre of mass coincides, at t=0, with the centre of mass of the spacecraft/PGB system the equations of motion read:
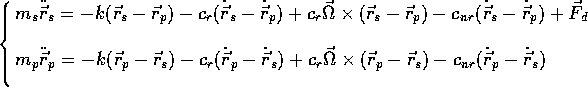
where 
is the mass of the spacecraft, 
the mass of the PGB, 
and 
are
the rotating and non rotating damping coefficients respectively, the
position vectors and velocities lie in the x,y plane and subscripts s
and p refer to the spacecraft and the PGB respectively. is known as rotating
damping coefficient because it is due to friction inside rotating parts of the
system.
is known as non-rotating damping coefficient because it is due to friction
inside non-rotating parts of the system. Note that and refer to two
physically different types of energy dissipation in the rotor and do not depend on the
reference frame (e.g., fixed or rotating) used to describe the problem (see Paper I, §6).
In GG there is no damping due to friction between rotating and non rotating parts
(referred to as friction in the bearings) because there is no motor, there are no
bearings and there are no non-rotating parts. Friction in the bearings is present in
ground based rotating machines and the corresponding torque tends to slow down the machine
(were not for the presence of the motor). Note that in the equations of motion of ground
based rotors the effect of friction in the bearings does not enter either, because the
motor supplies the energy required in order to maintain the spin rate of the system at its
nominal value. Friction in the bearings is therefore not relevant for these calculations,
neither in GG nor in ground machines and should not be confused with friction between
non-rotating parts (expressed by the non-rotating damping coefficient ) which has a
stabilizing effect. As for the coefficient used in the following, it should
be read as automatically multiplied by a safety factor 
slightly larger than 1 ( 
).
By applying the Fourier transform to the equations of the previous system we obtain the following linear system of equations:
The solutions of this system are:
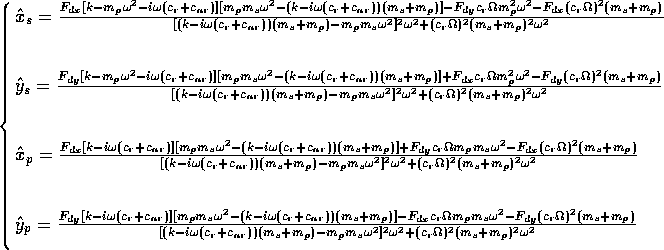
The transfer function for the GG spacecraft-PGB system is defined as:
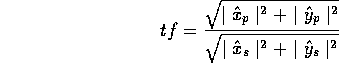
The mechanical coupling between the GG spacecraft and the PGB is 
, with a natural
frequency of oscillation 
. The mass of the spring is neglected. The
total energy dissipation due to rotating friction is expressed by the quality factor Q.
When in supercritical rotation, we use for the coefficient of rotating damping: 
(supercritical rotating damping), which would be incorrect if the system were dominated by
a large amount of rotating viscous damping. We have shown in Paper I (Appendix) that in
such a case the corresponding coefficient of rotating damping in the equations of motion
is given by 
with 
. Since this is certainly not the GG case,
a coefficient of the previous form (i.e. 
) can never be used in combination with a
value for the viscous quality factor ( 
in the GG spacecraft-PGB
case), but only with values 
(in point of fact it is 
for very small
viscous rotating damping and 
for an intermediate amount; see Paper I,
Appendix). To the contrary, the ESTEC Technical Reoport on GG (see its Appendix provided
on October 7 1996 at ESA HQ during the GG presentation) uses with Q=10, thus
implicitly making the assumption that the GG system be dominated by a very large amount of
rotating viscous friction. There is no physical grounds for such an assumption because
rotating damping in the GG system comes essentially from energy dissipated inside the tiny
springs when deformed at the spin frequency of 
and any contribution due to dissipation in
the rotating active dampers is very small because of the very small damping forces that
they are required to provide (see Paper I, Appendix and §3). Among the transfer functions
shown below we have computed also the case with Q=100; 
is the value measured
experimentally for a PGB prototype spring that we have manufactured carrying 3 wires for
signal transmission (see ``GG Pre Phase A Report'', ASI, September 1996).
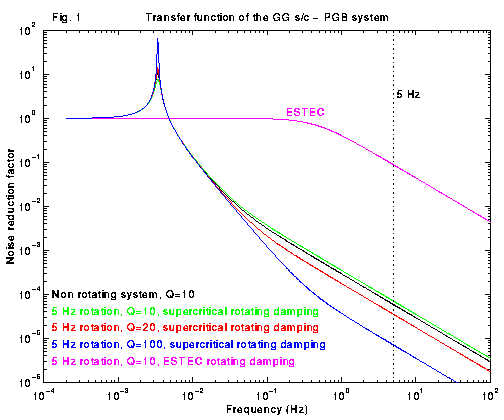
Figure 1: Transfer function of the GG spacecraft-PGB system in the
inertial reference frame for the cases of zero spin rate and supercritical rotation at . At
zero spin rate (black curve) the well known behaviour of passive noise attenuators on the
ground is recovered, where the height of the peak at the natural frequency is about Q.
In supercritical rotation we obtain the green, red and blue curves (for Q=10, 20
and 100 respectively) showing that the system is effective in attenuating vibrations at
the GG spin/signal frequency of (the higher the Q the better the
attenuation, which is peculiar of supercritical rotation). This means attenuation of
disturbances which act at w.r.t. the fixed frame, i.e. which are DC
or 
w.r.t. the rotating frame. The system is obviously transparent to
disturbances at frequencies below the natural one; in particular it is transparent to
effects which are DC w.r.t. the fixed frame (i.e. at w.r.t. the rotating one).
The ``ESTEC'' curve corresponds to a system in supercritical rotation dominated by a very
large amount of rotating viscous friction (see Paper I, Appendix); such a system would be
almost ineffective in attenuating vibrational noise.
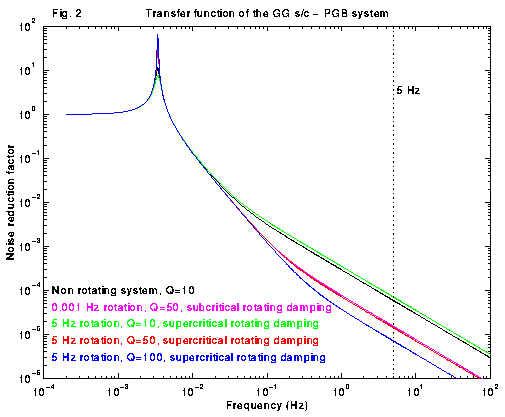
Figure 2: Transfer function of the GG spacecraft-PGB system in the
inertial reference frame at zero spin rate, in supercritical and in subcritical rotation
at and 
respectively. The coefficient of rotating
damping is 
for the supercritical case and 
for the subcritical one,
which is correct for the GG system. The black curve shows the transfer function at zero
spin rate and Q=10. The violet curve shows the transfer function of the system in
slow subcritical rotation with Q=50; the peak at natural frequency has height about
Q. The green, red and blue curves refer to the cases of fast supercritical rotation
with Q=10, 50 and 100 respectively; noise reduction of disturbances acting at
(w.r.t. the fixed frame) is apparent, a higher Q giving a better attenuation.
(Anna Nobili- nobili@dm.unipi.it)
