Let us calculate the transfer function of the GG spacecraft-PGB system which would be
measured by an observer rotating with the system at its angular speed 
. Instead of
re-casting the equations of motion in the body fixed reference system, we can obtain the
spectral coordinates in the rotating system from the inertial coordinates in the following
way:
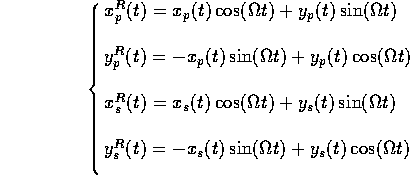
with 
, 
the inertial coordinates (i=p,s)
and 
, 
the body fixed coordinates. The spectral
coordinates are obtained operating the Fourier transform of the , .
Using 
and 
it is easy to find:
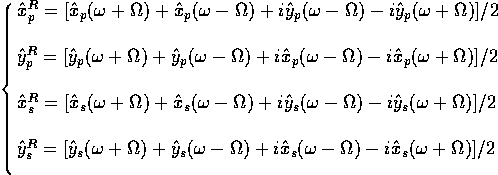
The transfer function is defined as:
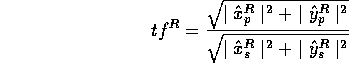
Figure 3: Transfer function of the GG spacecraft-PGB system in the
reference frame corotating with the system at zero spin rate and in supercritical
rotation. At zero spin rate (black curve) the transfer function is obviously the same as
in Fig. 1. In supercritical rotation (with the same coefficient 
as used in the
inertial reference frame) we obtain the green, red and blue curves, respectively for Q=10,
20 and 100. The peak at the spinning frequency shows that the passive noise attenuator
cannot change its properties just because we look at it in the rotating frame. It cannot
reduce vibrations at very low frequency w.r.t. the inertial frame, particularly the DC
ones; the observer corotating with the system sees these DC perturbations as 
, and
finds that the attenuator cannot reduce them, or better that it is transparent to
effects, where 
. Perturbations which are seen at by an inertial observer (and
attenuated), have frequencies 
and 
for the body fixed observer,
and in fact he too finds that they are attenuated. Like in Fig. 1, if we make the ESTEC
assumption that the system be dominated by a very large amount of rotating viscous
damping, we find that it is almost ineffective as noise attenuator.
(Anna Nobili- nobili@dm.unipi.it)
