1.1 Relevance of the
Equivalence Principle
"Galileo Galilei" (GG) is a small satellite
project devoted to testing the Equivalence Principle (EP) to 1 part in 1017, an improvement by 5 orders of magnitude over the best
results obtained so far on Earth. It is the same target of the STEP mission proposal as
evaluated twice by ESA at Phase A level within the competitions for the medium size
missions M2 (Blaser et al., 1993) and M3 (Blaser et al., 1996).
Do bodies of different composition fall
with the same acceleration in a gravitational field? If not, the so called Equivalence
Principle is violated. The Equivalence Principle, expressed by Galileo and later
reformulated by Newton, was assumed by Einstein as the founding Principle of general
relativity, the best theory of gravitation available so far. In fact, it is not a
Principle but a starting hypothesis unique to Gravity: no Equivalence Principle holds for
the other fundamental forces of nature (the electromagnetic, weak and strong interaction)
and almost all theories trying to unify gravity with these forces require the Equivalence
Principle to be violated, thus indicating that general relativity may not be the final
truth on gravitation, just as Newton’s theory of gravitation was proved by
Einstein not to be the final truth at beginning of this century. All tests of
general relativity, except those on the Equivalence Principle, are concerned with specific
predictions of the theory; instead, EP tests probe the basic assumption of general
relativity, and this is why they are a much more powerful instrument of investigation. A
high accuracy, unquestionable, experimental result on the Equivalence Principle - no matter whether it is violated or confirmed-
will be a crucial asset for many decades to come. And this is how it has to be, because
physics is an experimental science in which any theory, in spite of its internal
consistency and beauty, has to confront experiments, and ultimately will stand or fall
depending solely on experimental results.
Galileo questioned Aristotle’s statement that heavier bodies
should fall faster than lighter ones, arguing instead that all bodies fall at equal speeds
regardless of their mass and composition (this is the Universality of Free Fall).
His formulation of the universality of free fall, which lately became known as the
Equivalence Principle, was first published in 1638
:
"…veduto, dico questo, cascai in opinione
che se si levasse totalmente la resistenza del mezzo, tutte le materie descenderebbero con
eguali velocitŕ " ("... having observed this I came to the conclusion that, if
one could totally remove the resistance of the medium, all substances would fall at equal
speeds "). It appeared in his Discorsi e dimostrazioni matematiche intorno a
due nuove scienze attinenti alla meccanica e ai movimenti locali, which was published
outside Italy (in Leiden) few years after completion due to Galileo’s prosecution by
the Church of Rome (Galileo, Le Opere, Vol. VIII, 1968 Edition). Aged 74, Galileo
was blind and under house arrest; but the Discorsi are based on much earlier work, mostly on experiments with the
inclined plane and the pendulum going back almost 40 years to the time when he was a young
lecturer at the University of Pisa or had just moved to Padova. Galileo was well aware
that experiments he made with inclined plane and pendula were much more accurate than just
dropping masses from a tower; but mass dropping experiments allowed him to describe the
universality of free fall in a very straightforward manner, not requiring a deep
understanding of mechanics. This is how Galileo has become known worldwide for his mass
dropping experiments. Indeed, no image of science has captured the imagination of ordinary
people more than that of Galileo dropping masses from the leaning tower of Pisa, a symbol
of the birth of the modern scientific method.
About 80 years after Galileo's first experiments Newton went
further, actually recognizing the proportionality of
mass and weight. Newton regarded this proportionality
as so important that he devoted to it the opening paragraph of the Principia
(Cajori Edition, 1934) where he stated: " This quantity that I mean hereafter under the name of ...
mass ... is known by the weight ... for it is proportional to the weight as I have found
by experiments on pendulums, very accurately made... ''
. At the beginning of the 20th century,
almost 300 years since Galileo's work, Einstein realized that because of the
proportionality between the gravitational (passive) mass mg and the inertial mass mi, the effect of gravitation is locally equivalent to the effect of an
accelerated frame and can be locally cancelled: this is known as the Weak Equivalence
Principle which Einstein introduced in 1907 (Einstein, 1907) as the hypothesis of
complete physical equivalence between a gravitational field and an accelerated
reference frame: in a freely falling system all masses fall equally fast, hence
gravitational acceleration has no local dynamical effects. Einstein then generalized this
principle to the Strong Equivalence Principle, on which he based his theory of general
relativity. The Strong Equivalence Principle states that in an electromagnetically
shielded laboratory, freely falling and non rotating, the laws of physics - including their numerical content- are
independent of the location of the laboratory. In such a laboratory all particles free of
non gravitational forces move with the same acceleration. Therefore, according to
Einstein, the effects of gravity are equivalent to the effects of living in a curved
space-time. In this sense the Equivalence Principle expresses the very essence of General
Relativity and as such it deserves to be tested as accurately as possible. In the last 30
years since the advent of the space age general relativity has been subject to extensive
experimental testing as never before in its first 50 years of existence, and so far it has
come out having no real competitors; the crucial area where experimental gravitation is
likely to play an important role is in the verification of the universality of free fall
as a test of the weak equivalence principle itself, since it is tantamount to testing
whether gravitation can be ascribed to a metric structure of space-time.
The total mass-energy of a body can be expressed as the sum of many
terms corresponding to the energy of all the conceivable interactions and components:
m = S k mk. The adimensional Eötvös parameter h = 2[(mg/mi)A - (mg/mi)B]/[(mg/mi)A
+ (mg/mi)B]
which quantifies the violation of equivalence for two bodies of composition A and B, inertial mass mi and gravitational mass mg, can be generalized into
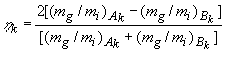 (1.1)
(1.1)
such that a non-zero value of h k
would define the violation of equivalence between the inertial and gravitational
mass-energy of the
k-th
type. For instance, the rest mass would contribute (as a fraction of the total) for @ 1;
the nuclear binding energy for 8× 10-3, the mass difference between neutron and proton for 8× 10-4 (A-Z) (A being the number of protons plus neutrons and Z the number of protons in the nucleus), the electrostatic
energy of repulsion in the nuclei for 6×
10-4 Z2 A-4/3, the
mass of electrons for 5× 10-4 Z, the antiparticles for @ 10-7, the weak interactions
responsible of b decay for @ 10-11. From the point of
view of conventional field theory, the verification of all these separate Equivalence
Principles corresponds to a very peculiar coupling of each field to gravity; whether
and why it should be so in all cases is a mystery. Let us consider the case of
antiparticles. A peculiarity of gravity, strictly related to the Equivalence Principle, is
that there is so far no evidence for antigravity, namely for the possibility that matter
is gravitationally repelled by antimatter. A negative ratio of inertial to gravitational
mass would obviously violate the Equivalence Principle and forbid any metric theory of
gravity. Yet, there are theoretical formulations which would naturally lead to
antigravity. Unfortunately, while experiments concerning the inertial mass of
antiparticles have been highly successful, and these are very accurately known,
gravitational experiments (i.e. involving the gravitational mass of antiparticles) are
extremely difficult because of the far larger electric effects, such as those due to stray
electric fields in the drift tube. In absence of such direct tests, an improvement by
several orders of magnitude of current tests of the weak Equivalence Principle with
ordinary matter would also be an important constraint as far as the relation between
gravity and antimatter is concerned.
Nearly all attempts to extend the present framework of physics predict
the existence of new interactions which are composition dependent and therefore violate
the Equivalence Principle. Equivalence Principle tests are by far the most sensitive low
energy probes of such new physics beyond the present framework. This is because any
deviation from the universality of free fall - expressed as a
fractional differential acceleration D
a/a between falling bodies of different composition-
is proportional to the post-Newtonian deviations from general relativity measured, for
instance, by the adimensional parameter g *ş g -1 (g the Eddington parameter) with a proportionality factor <<1 (from 10-5 to 10-3 depending on scalar or vector models). Therefore, while g *
is constrained by post-Newtonian or pulsar tests below 10-3, the current ground results on the Equivalence Principle giving D a/a Ł 10-12 already constrain g * below 10-7 or 10-9, which clearly shows the superior probing power of Equivalence
Principle tests.
No precise target accuracy at which a violation should occur has been
predicted by these theories; an EP violation is expected, but only below the
10-12 level reached so far,
probably well below it; whether this is really so, only high accuracy experiments can
tell.
1.2 The Advantages of
Space
An EP space experiment in low Earth orbit
offers the crucial advantage of a signal about a factor of a thousand bigger than on Earth
(see Sec. 3.2); the challenge of a fully automated remote controlled experiment can be
traded off against the advantages of weightlessness. An accuracy of
1 part in 1017 in EP testing means five orders of magnitude improvement with
respect to the best ground results. Even with further progress in ground experiments (e.g.
to an accuracy of 1 part
in 1013,
possibly 1014)
a space mission would undoubtedly mean a great leap forward allowing space scientists to
probe a totally unknown, highly promising field of physics like no other ground experiment
can even dream of.
1.3 History of
Equivalence Principle Testing
Aristotle’s statement that heavier bodies should fall
faster than lighter ones was already questioned in the 6th century by Philoponus, who noted that: if two bodies are released
by the same altitude one can observe that the ratio of the times of fall of the bodies
does not depend on the ratio of their weights, and the difference of the times is very
small. Amazingly enough, it was only in 1553 that Benedetti reconsidered the issue,
stating that the velocity of fall does not depend on the weights of the falling bodies.
Galileo questioned Aristotle’s view
and even showed the internal contradiction of Aristotle’s reasoning with a simple
argument which goes as follows: If then we take two bodies whose natural speeds are
different, it is clear that on uniting the two, the more rapid one will partly be retarded
by the slower, and the slower will be somewhat hastened by the swifter….Hence the
heavier body (made by the two tied together) moves with less speed than the lighter
(the former swifter one); an effect which is
contrary to your (by Aristotle) supposition. More importantly, Galileo was well
aware of the need to provide experimental evidence. By dropping bodies of different
composition in media much denser than air Galileo came to the conclusion that all bodies
fall equally fast and that any observed difference is due to the different resistance of
the medium that different bodies are subject to. Galileo was also aware of the difficulty
to prove this fact by dropping masses from a height. As he clearly argues in the Discorsi, from a big height
the accumulated effect of air resistance is too large to allow a reliable conclusion,
while from a small one any difference is too small to appreciate. Most probably Galileo
was not able to calculate precisely the effect of air resistance, but he certainly knew
that it was much smaller if the velocity of the body was small (we know it is proportional
to the velocity squared). He therefore performed experiments with bodies falling on
inclined planes where only a fraction of the gravitational acceleration is relevant, which
reduces the falling velocity - hence also the effect of air
resistance.
Better still than bodies falling on inclined planes are bodies
suspended from a wire and brought to oscillation like a pendulum: if all bodies fall with
the same acceleration in the gravitational field of the Earth, bodies suspended from wires
of the same length which are released at the same time by the same angle must keep in step
regardless of their mass or composition. Besides reducing the velocity -
and air resistance- the periodic repetition of the motion
allows a better measurement and improves the accuracy of the experiment. …e
finalmente ho preso due palle, una di piombo e una di sughero, quella ben piů di cento
volte piů grave di questa, e ciascheduna di loro ho attaccata a due sottili spaghetti
eguali, lunghi quattro o cinque braccia, legati ad alto; allontanata poi l’una e
l’altra palla dallo stato perpendicolare, gli ho dato l’andare nell’istesso
momento, ed esse, scendendo per le circonferenze de’ cerchi descritti da gli spaghi
eguali, lor semidiametri, passate oltre al perpendicolo, son poi per le medesime strade
ritornate indietro e reiterando ben cento volte per lor medesime le andate e le tornate,
hanno sensatamente mostrato, come la grave va talmente sotto il tempo della leggiera, che
né in ben cento vibrazioni, né in mille, anticipa il tempo d’un minuto secondo, ma
camminano con passo egualissimo.
Pendulum experiments have provided the most accurate tests of the
Equivalence Principle till the torsion balance was used for EP testing at the beginning of
1900. Newton is often reported as the first ever to perform pendulum tests of the
Equivalence Experiment; in fact, Galileo’s pendulum experiments as in the above
quotation from the Discorsi had even been reported much earlier than the
publication of the Discorsi, in a letter addressed by Galileo to Guidobaldo dal
Monte in 1602 (Le Opere, Vol. X, 1968 Edition). It is sometimes argued that Galileo
could not perform accurate pendulum tests of the Equivalence Principle because - although he had discovered the physical properties of the pendulum- he did not have an accurate pendulum clock, which was invented by
Christian Huygens after Galileo’s death, in 1657. Huygens clock was obviously
available to Newton. The point is, however, that pendulum tests of the Equivalence
Principle do not require a clock: the oscillating bodies must keep in step, and only
differences between the two matter, not the precise value of the oscillation period.
Newton quotes his pendulum tests of the Equivalence Principle to have an accuracy of
1 part in 103. The pendulum tests described by Galileo have been repeated by
Fuligni and Iafolla (1993). They concluded that even without special care it is easy to
reach an accuracy of 1
part in 103; an
error by 0.1% in the
length of the suspensions is a realistic assumption, yielding a similar accuracy for the
outcome of the experiment, and this is in agreement with Galileo’s observation that
the bodies keep in step for hundred or even thousands swings.
Experiments to test the Equivalence Principle require to measure a differential
effect between the test bodies; a pendulum experiment is better than a mass dropping
experiment because it makes it easier to record differences, but it is not a null
experiment. An apparatus for EP testing should be differential by its own design, i.e.
such that it gives a non-zero signal only in case of violation; otherwise it should give a
null result. The torsion balance is one such differential device: two objects of different
composition are connected by a rod and suspended in a horizontal orientation by a thin
wire. Any suspended body is subject to the gravitational attraction of the Earth and to
the centrifugal force due to the Earth daily rotation about its axis. In the horizontal
plane the two reach equilibrium along the North-South direction. The gravitational
attraction is proportional to the gravitational mass
mg, while the centrifugal force is proportional to the inertial
mass mi. If the
ratio mg/mi is different for the two bodies of the torsion balance there is differential
force in the North-South direction; with the rod of the balance aligned along the
East-West direction the entire differential force gives a torque tending to twist the
torsion balance. The differential force and its torque are constant; by exchanging the
bodies on the balance (or rotating the apparatus by 180° ), the sense of twist
should reverse. If the ratio mg/mi is the same for the two bodies (no violation) the torsion balance
should give no twist (null result).
The first careful tests of the Equivalence Principle with a torsion
balance were performed over many years at the beginning of this century by Roland von
Eötvös and his colleagues in Budapest. Their results were published three years after
Eötvös’ death (Eötvös et al., 1922) and more details on the apparatus and
methods of measurement appeared in Eötvös’ collected works (Eötvös, 1953); the
experiments were later repeated by Renner (1935) using Eötvös’ apparatus. Most
precise experiments are null experiments, and the Eötvös experiment is no exception:
they reported no EP violation to the level of several parts in
109, an accuracy much better than in all previous experiments.
Eötvös results have remained unchallenged until the 60’s, when
an Eötvös-type experiment was performed in Princeton (Roll et al. 1964) with an
essential novelty. On the footsteps of Eötvös outstanding results the Princeton
scientists led by Robert Dicke also used a torsion balance. However, Eötvös original
experiment, despite its high quality, has an essential weakness: the signal is a constant
twist produced by a constant torque (DC effect), hence the experiment lacks a suitable
control, for there is no way of turning off the centrifugal force of the Earth’s
diurnal rotation. Only a
180° rotation of the apparatus by the experimentalists (with the
inevitable consequence of disturbing the delicate balance) gives the signal a signature.
Dicke suggested to look at the acceleration of the apparatus towards the Sun, rather than
the Earth, and compare it with the centrifugal force due to the annual rotation of the
Earth around the Sun. Were the ratio mg/mi different for the weights of the balance, an anomalous torque
would appear; at 6 a.m. and 6 p.m., and for a torsion balance beam in the North-South
direction, an anomalous gravitational pull upon one of the weights at an end of the beam
would produce a turning force. The resulting twist would be periodic with a 24-hr period (the solar day) due to the
diurnal rotation of the Earth. The horizontal component of the acceleration towards the
Sun (as well as of the annual centrifugal acceleration) is - at
most- 3/8 of the diurnal centrifugal acceleration, but it is modulated by the rotation of
the Earth with a 24-hr period and therefore the measurement contains its own zero
check. Thanks to this frequency modulation and in spite of the weaker signal Roll et
al. (1964) improved significantly Eötvös result, finding no EP violation to about 1
part in 1011 for aluminum and gold. Braginsky and Panov (1973) also used the
Sun as a source and the modulation of the Earth’s rotation. They improved the
experiment further using 8 masses (of aluminum and platinum) at the vertices of an
octagon, instead of two. The torsion-balance experiment being a small force experiment,
any spurious gravitational field due to nearby masses can cause significant disturbances.
The geometrical structure realized by Braginsky and Panov is less sensitive to the effects
of such fields, since only a gravitational potential with a non-zero fifth derivative does
affect their balance. The result of their experiment is that the inertial and
gravitational mass (for aluminum and platinum) are the same to about 1 part in 1012.
The advantage of a space experiment (with a much stronger signal) was
recognized soon after the beginning of the space age. While designing a space experiment
scientists also tried to provide a frequency modulation. Chapman and Hanson (1970)
proposed to test the Equivalence Principle in space using a fast rotating platform so as
to modulate the signal at its rotating frequency; however, in their apparatus the test
bodies were constrained to move along one diameter of the rotating platform, and it is
well known that any such rotating system is always strongly unstable above the critical
speed (Den Hartog, 1985). Worden and Everitt (1973) proposed instead that the orbital
motion of the spacecraft enclosing the test bodies would provide the modulation. This
requires the spacecraft (which carries the coaxial test cylinders) to be kept fixed with
respect to inertial space by accurate active control. This is the STEP proposal (Worden
and Everitt, 1973; Worden, 1976; Worden, 1987; Blaser et al., 1993; Blaser et al.
1996). The symmetry axis of the test cylinders is the sensitive axis, and lies in the
orbital plane (the system is very stiff in the plane perpendicularly to the symmetry
axis). If one cylinder is attracted by the Earth more than the other there is a relative
movement of the two one inside the other; the effect is maximum when the symmetry axis is
directed towards the center of the Earth (changing sign as the satellite moves by 180° around the Earth) and it is zero when the symmetry axis is
perpendicular to the satellite-to-Earth direction. Hence, the signal has an intensity
varying at the orbital frequency of the satellite (corresponding to a period, in low Earth
orbit, of about
6,000 sec).
Any higher frequency signature, higher than the orbital frequency, that one would wish to
impress on the signal requires the spacecraft to be spun around its actively controlled
space-fixed attitude. Due to the STEP design these can only be slow rotations and require
a careful active control.
In the meantime scientists have achieved a higher frequency modulation
of the putative EP violation signal in classical torsion balance experiments where the
apparatus is mounted on a turntable that rotates with a period of
1¸ 2 hr. These are the very
careful EP experiments by the "Eöt-Wash" group at the University of Seattle (Su
et al., 1994) whose results are at present the most accurate (to about 1 part in 1012). Their modulation frequency is the highest achieved so far, and
their ongoing attempts to improve the sensitivity by one order of magnitude include a
faster and smoother rotation of the turntable. The only alternative to attempting faster
rotation is pursued by the R. Cowsik group in India, with a much heavier torsion balance
in a very low noise environment (25 m under the ground) and a very good thermal stability (by means of
two, very large, concentric vacuum chambers) (Unnikrishnan, 1994; Cowsik et al.,
1997)
It is apparent how all EP differential experiments based on the direct
measurement of extremely small displacements between two test bodies have been driven, in
Earth-based experiments as well as in space proposals, by the need to provide a modulation
frequency of the expected tiny signal at the highest possible frequency. GG tries to go
much beyond in this trend by modulating the signal at
2 Hz, an increase by more than a factor 104
in comparison to all previous experiments. A modulation
frequency of @ 1 Hz has been proposed also for an Equivalence Principle experiment
inside a capsule in sub-orbital flight with a free falling time of @
30 sec (Lorenzini et
al., 1994; Iafolla et al.,1998).
Surprisingly enough, completely different tests of the Equivalence
Principle (for the Earth and the Moon falling towards the Sun) have achieved an accuracy
close to that of torsion balance experiments, even about one order of magnitude better
(Dickey et al. 1994; Williams et al., 1996). The Earth-
Moon distance is measured by lunar laser ranging (LLR) to the corner cube laser reflectors
left by the astronauts on the surface of the Moon, accurate to better than 1 cm. Were the
Earth and the Moon to be attracted differently by the Sun because of their different
composition (
1/3 iron core
and 2/3 silicate mantle
the Earth; entirely silicate mantle the Moon), a physical model based on conventional
Newtonian gravity with general relativistic corrections would not be able to make
predictions reconcilable with the observed LLR data. This is a test of the Equivalence
Principle for different composition, but also for gravitational self-
energy effects in the Earth (testing gravity's pull on gravitational energy), effects
which are obviously absent in test bodies of laboratory size. According to Einstein, all
forms of matter and energy, including the gravitational binding energy, accelerate at the
same rate in a uniform gravitational field, and the gravitational binding energy of the
earth amounts to 5× 10-10 of its mass and is therefore not negligible to the current achieved
accuracy. However, it should be emphasized that - despite the
high quality of the analysis- LLR tests of the Equivalence
Principle are based on highly complex physical models of many perturbing effects on the
orbit of the Moon (such as tides) whose signature can be the same as that of an EP
violation, and which involve many unknown parameters to be adjusted. To the contrary, EP
experiments with test bodies of laboratory size can always provide a zero check: no
sensitivity can be claimed better than the one which is obtained using in the same
apparatus test bodies of the same composition.
1.4 Novelties and Advantages
of the GG Design
A torsion balance is not well suited for
testing the Equivalence Principle in space, where scientists agree to use coaxial test
cylinders, with a read out system to detect relative displacements between them. The main
novelty of GG is to modulate the expected EP violation signal by spinning the entire
spacecraft (also of cylindrical symmetry, enclosing the test bodies and the read- out sensors) at
2 Hz, which in addition provides 1-axis passive stabilization of the satellite.
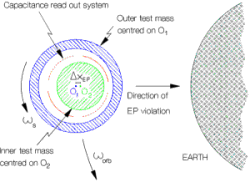
Figure 1.1 (not to scale) Section of the
GG coaxial test cylinders and capacitance sensors in the plane perpendicular to the spin
axis. They spin at angular velocity w
s while orbiting around the Earth at angular velocity w orb. The capacitance plates of the read-out are shown in between
the test bodies, in the case in which the centers of mass of the test bodies are displaced
from one another by a vector  due to an
Equivalence Principle violation in the gravitational field of the Earth (e.g., the inner
test body is attracted by the Earth more than the outer one because of its different
composition). Under the (differential) effect of this new force the test masses, which are
weakly coupled by mechanical suspensions, reach equilibrium at a displaced position where
the new force is balanced by the weak restoring force of the suspension, while the bodies
rotate independently around O1 and O2 respectively. The vector of
this relative displacement has constant amplitude (for zero orbital eccentricity) and
points to the center of the Earth (the source mass of the gravitational field). The signal
is therefore modulated by the capacitors at their spinning frequency with respect to the
center of the Earth.
due to an
Equivalence Principle violation in the gravitational field of the Earth (e.g., the inner
test body is attracted by the Earth more than the outer one because of its different
composition). Under the (differential) effect of this new force the test masses, which are
weakly coupled by mechanical suspensions, reach equilibrium at a displaced position where
the new force is balanced by the weak restoring force of the suspension, while the bodies
rotate independently around O1 and O2 respectively. The vector of
this relative displacement has constant amplitude (for zero orbital eccentricity) and
points to the center of the Earth (the source mass of the gravitational field). The signal
is therefore modulated by the capacitors at their spinning frequency with respect to the
center of the Earth.
The figure above shows, in the plane perpendicular to the spin/symmetry
axis, how the GG coaxial test cylinders (of different composition) would move one with
respect to the other were they attracted differently by the Earth because of an EP
violation. The Figure shows the test cylinders one inside the other and two pairs (for
doubling the output data) of capacitance plates in between them to measure any relative
displacement. If one of the bodies is attracted by the Earth more than the other, the two
centers of mass move away from one another always towards the center of the Earth. In GG
the test cylinders are coupled by very weak mechanical suspensions so that even a tiny
differential force (in the plane perpendicular to the spin/symmetry axis) causes a
mechanical displacement which is detectable once transformed into an electric potential
signal by the capacitance read-out. The weaker the coupling, the longer the natural period
of differential oscillations of the test bodies, the more sensitive the system is to
differential forces such as the one caused by an EP violation. It is apparent from Fig.
1.1 that spinning capacitance plates modulate the amplitude of the electrical signal
caused by an EP violation at their spinning frequency with respect to the Earth (
2 Hz in the current baseline), with a
well defined phase (the vector does always point towards the center of the Earth). In
absence of spin the EP violation force has constant intensity (except for the effect of
orbital eccentricity of the satellite, which is close to zero) and a direction changing at
the orbital frequency of the satellite around the Earth (@ 1.75× 10-4 Hz); so in GG the electric signal is modulated at a frequency about 104 times higher than the
frequency of the EP violation force, the advantage being the reduction of low frequency
noise both mechanical (the suspensions have higher mechanical quality factor Q at higher frequency) and electrical
(lower 1/f electronic
noise). The spinning state of the GG spacecraft is a stable 1-axis rotation and needs no active control.
An important consequence of the fact that in GG the expected EP
violation force lies in the plane normal to the spin/symmetry axis of the test cylinders
is that a major perturbation due to the so called "radiometer effect" is zero
also at room temperature. It is known that, in low pressure conditions where the mean free
path of the gas particles is much larger than the dimensions of the vessel, a cylinder
whose faces are not at the same temperature is subject to an acceleration along its
symmetry axis whose value is exceedingly large unless the residual gas pressure is
extremely low, down to values which can only be obtained at very low temperatures. In STEP
this radiometer effect along the symmetry/sensitive axis of the test cylinders competes
directly with the signal, and is reduced thanks to the extremely low level of residual
pressure, which can be obtained by operation at superfluid
He temperature (about 2 K). Instead, a hollow cylinder whose inner and outer surfaces were
not exactly at the same temperature, would have zero radiometer effect in the plane
perpendicular to its axis, for pure symmetry reasons. In reality, azimuth asymmetries as
well as the radiometer effect along the symmetry axis of the cylinders must be taken into
account in GG, since it is a non cryogenic experiment; however, the requirements they
impose on the amount of acceptable temperature gradients are compatible with a pure
passive thermal control of the GG experimental apparatus (see Sec. 2.2.3). If the
radiometer effect is dealt with at room temperature, one of the main reasons why a high
accuracy EP experiment in space should be operated in cryogenic conditions is no longer
valid.
Low temperature is certainly helpful in reducing thermal noise. Since
the dependence of thermal noise acceleration on the experiment temperature
T and the mass m of the test bodies is µ (T/m)1/2, in GG we use more
massive test bodies: test masses of 10 kg each at 300 K, as we have in GG, result in the same thermal noise as with test
masses of 0.1 kg at a
temperature of 3 K.
However, a future, lower temperature version of the GG experiment can be envisaged for
which the rapid spin gives an important advantage: the very high centrifugal force at the
periphery of the spacecraft would dominate the motion of the refrigerating (movable)
material and largely reduce, by symmetry, its perturbations on the bulk of the experiment;
evaporation can take place along the spin axis for symmetry reasons too. This is unlike
non-spinning or slowly spinning satellite experiments for EP testing in which
perturbations from the nearby refrigerant mass (a few hundred liters of He in STEP) is known to be a serious
source of perturbation.
The weak mechanical coupling of the GG test bodies (e.g. obtained with
a simple and effective use of helical springs and flat gimbals pivoted on thin torsion
wires) is the key feature which allows us to cope with a major dangerous effect: the
effect of residual air drag along the satellite orbit. Air resistance acting on the
spacecraft surface is experienced by the test bodies suspended inside it as a
translational inertial acceleration equal and opposite to the one caused by air drag on
the center of mass of the whole satellite (spin axes are stable due to the extremely high
energy of spin). This acceleration is about 8 orders of magnitude weaker than
1-g on Earth but about as many orders
of magnitude larger than the expected signal; it should be the same on both test
cylinders, but only in the ideal case that their masses and suspensions were exactly the
same. Drag-free control (with FEEP ion thrusters) of the GG spacecraft reduces the
corresponding inertial acceleration on the payload. In order to further reduce its
differential effect on the test cylinders due to small differences in their suspensions,
the test cylinders are coupled similarly to the two weighs of an ordinary balance whose
arms can be adjusted (by means of piezoceramic actuators) so as to eliminate differential
effects. Balancing of weights (under local gravity) is obviously well known on Earth,
where weights can be balanced to 1 part in 108 or better, much more accurately than it is required for the GG test bodies. It
is also well known that small forces are much easier to balance than large ones; hence,
since in the GG spacecraft the largest force (due to air drag) is many orders of magnitude
weaker than local gravity on Earth, balancing the test bodies must be easier than on Earth
by far, where it has been tested on the payload prototype. To be balanced is a property of
the system, not of the particular force acting on it; hence, all other common mode
perturbations beside drag (e.g. solar radiation pressure) are also balanced once the main
drag effect is balanced. Balancing the drag does not eliminate an EP violation signal
because it is a differential and constant signal while drag produces common mode forces,
is variable in time and about 90° out of phase with respect to the EP violation signal. Vibration
noise close to the spin frequency (e.g. from the FEEP thrusters) is attenuated by the
suspensions of the laboratory enclosing the test bodies.
Drag- free control of GG with FEEP thrusters
requires a negligible amount of propellant, amounting to only several grams for the entire
duration of the mission. By contrast, the He thrusters planned for STEP require a few
hundred liters of He on board, whose mass is in itself a disturbing source for the
experiment. FEEP thrusters are electrically tuned; instead, He thrusters are tuned
mechanically. Because of their numerous advantages, particularly the extremely low
propellant mass, FEEP have been proposed also for STEP (Blaser et al., 1994), but
the presence on board of a considerable mass of superfluid He and the consequent need to
eliminate the boiled off He from the dewar in a carefully controlled manner, clearly
require
He thrusters,
which are therefore used also for drag- free control rather
than adding the FEEP. The superiority of FEEP in small force gravitational missions is
beyond question; they are the current baseline choice not only for GG but also for LISA
and OMEGA, two mission proposals for the detection of gravitational waves in space.
The GG bodies all spin at a frequency much higher than their natural
frequencies of oscillation (which are very low because of the very weak suspensions that
can be used in absence of weight). This state of rotation is very close to that of ideal,
unconstrained, rotors and allows the test cylinders to self-center very precisely (the
center of mass of an ideal free rotor would be perfectly centered on the spin axis). This
is how it is possible to reconcile a high frequency of spin (hence a high frequency
modulation of the signal) with the need to measure extremely small relative displacements.
However, suspensions are not perfect, which means that, as they undergo deformations at
the frequency of spin, they also dissipate energy. The higher the mechanical quality of
the suspensions, the smaller the energy losses. Small energy losses are known to produce
slow whirl motions of the suspended bodies one around the other which must be damped
actively, with small capacitance sensors/actuators and appropriate control laws (see Chap.
6). In fact, whirl motions of the
GG test cylinders are so slow that they can be damped at time intervals long enough to
allow data taking in between, when active damping can be switched off.
Unlike STEP, GG has mechanical suspensions and no floating bodies; they
are all connected by mechanical conductive suspensions which once coated with the same
conductive material provide a "Faraday cage" and consequent electrical
discharging of the experimental apparatus. This is a major advantage because the electric
forces caused by even a limited amount of charge (in the Van Allen belts and South
Atlantic Anomaly) are enormous compared to the very small gravitational force to be
detected; apart from the discharging mechanism to be devised, the electric charge acquired
by the test bodies needs to be measured before discharging, which in itself is a source of
perturbation. No such devices are needed in GG.
It is clear that fast rotation and weak mechanical suspensions are the
main features of the GG experiment design, distinguishing it from the STEP design. Other
advantages of fast rotation beside the modulation of the signal are that a large number of
perturbing effects (e.g. due to in-homogeneity of the test bodies, spacecraft mass
anomalies, non-uniform thermal expansion, parasitic capacitances, etc.) appear as DC
because the entire system is spinning.
Last but not the least, the GG payload design can be tested on the
ground (see Chap.
3). An
important novel feature of the GG space experiment is that it is sensitive to differential
forces in the plane perpendicular to the spin/symmetry axis of the test cylinders (as in
the case of an Equivalence Principle violation). If the test masses are suspended on the
surface of the Earth a violation of the Equivalence Principle can be detected as a force
in the horizontal plane along the North/South direction; the GG test cylinders can be
suspended along the vertical/symmetry axis and yet be sensitive to differential forces in
the horizontal plane. The suspensions must necessarily be strong along the vertical, to
sustain the weight of the bodies, but it is possible to couple the cylinders weakly so
that they can respond by a measurable displacement (measurable with a capacitance read- out at room temperature, like in GG) to tiny differential forces
acting between them in the horizontal plane. The result is very important: despite the
weaker EP violation signal (by about 3 orders of magnitude) and the unfavorable 1-g environment, the GG payload design can be tested on the ground to
the same level of measurement sensitivity which is required by the GG mission in space.
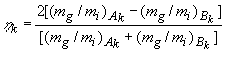 (1.1)
(1.1) (1.2)
(1.2)