


Paper published on New
Astronomy, 10 March 1998; 3(3) 175-218 (PDF file)
Proposed noncryogenic, nondrag-free test of the equivalence principle in space
[a] A.M. Nobili *
[a] D. Bramanti *
[a] G. Catastini *
[b] E. Polacco *
[c] G. Genta *
[c] E. Brusa *
[d] V.P. Mitrofanov *
[e] A. Bernard
[e] P. Touboul *
[f] A.J. Cook
[g] J. Hough *
[h] I.W. Roxburgh *
[h] A. Polnarev *
[i] W. Flury *
[j] F. Barlier *
[e] C. Marchal
[a] Gruppo di Meccanica Spaziale, Dipartimento di Matematica, Universitŕ di Pisa, Via F.
Buonarroti 2, I-56127, Italy
[b] Dipartimento di Fisica, Universitŕ di Pisa, Piazza Torricelli 2, I-56100, Italy
[c] Dipartimento di Meccanica, Politecnico di Torino, Italy
[d] Department of Physics, Moscow State University, Russia
[e] ONERA, Chatillon, France
[f] Selwyn College, Cambridge, UK
[g] Department of Physics and Astronomy, University of Glasgow, UK
[h] Astronomy Unit, Queen Mary and Westfield College, London, UK
[i] ESOC, Darmstadt, Germany
[j] CERGA, Grasse, France
Received 3 April 1997; accepted 9 September 1997
Communicated by Francesco Melchiorri
Abstract
Ever since Galileo scientists have known that all bodies fall with the
same acceleration regardless of their mass and composition. Known as the Universality
of Free Fall, this is the most direct experimental evidence of the Weak Equivalence
Principle, a founding pillar of General Relativity according to which the
gravitational (passive) mass  and the inertial mass
and the inertial mass 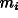 are always in the same positive ratio in all test bodies. A space
experiment offers two main advantages: a signal about a factor of a thousand bigger than
on Earth and the absence of weight. A new space mission named GALILEO GALILEI (GG) has
been proposed (Nobili et al., 1995; GALILEO GALILEI, 1996) aimed at testing the
weak Equivalence Principle (EP) to 1 part in
are always in the same positive ratio in all test bodies. A space
experiment offers two main advantages: a signal about a factor of a thousand bigger than
on Earth and the absence of weight. A new space mission named GALILEO GALILEI (GG) has
been proposed (Nobili et al., 1995; GALILEO GALILEI, 1996) aimed at testing the
weak Equivalence Principle (EP) to 1 part in 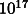 in a rapidly spinning (
in a rapidly spinning (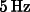 )
drag-free spacecraft at room temperature, the most recent ground experiments having
reached the level of
)
drag-free spacecraft at room temperature, the most recent ground experiments having
reached the level of 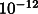 (Adelberger et al., 1990; Su et al., 1994). Here we present a nondrag-free
version of GG which could reach a sensitivity of 1 part in
(Adelberger et al., 1990; Su et al., 1994). Here we present a nondrag-free
version of GG which could reach a sensitivity of 1 part in  . The main feature of GG is that, similarly to the most recent
ground experiments, the expected (low frequency) signal is modulated at higher frequency
by spinning the system, in this case by rotating the test bodies (in the shape of hollow
cylinders) around their symmetry axes, the signal being in the perpendicular plane. They
are mechanically suspended inside the spacecraft and have very low frequencies of natural
oscillation (due to the weakness of the springs that can be used because of
weightlessness) so as to allow self-centering of the axes; vibrational noise around the
spin/signal frequency is attenuated by means of mechanical suspensions. The signal of an
EP violation would appear at the spin frequency as a relative (differential)
displacement of the test masses perpendicularly to the spin axis, and be detected by
capacitance sensors; thermal stability across the test masses and for the required
integration time is obtained passively thanks to both the fast spin and the cylindrical
symmetry. In the nondrag-free version the entire effect of atmospheric drag is retained,
but a very accurate balancing of the test bodies must be ensured (through a coupled
suspension) so as to reach a high level of Common Mode Rejection and reduce the
differential effects of drag below the target sensitivity. In so doing the complexities of
a drag-free spacecraft are avoided by putting more stringent requirements on the
experiment. The spacecraft must have a high area-to-mass ratio in order to reduce the
effects of nongravitational forces; it is therefore a natural choice to have three pairs
of test masses (in three experimental chambers) rather than one as by Nobili et al. (1995) and the (mission called GALILEO GALILEI, 1996). The GG setup is
specifically designed for space; however, a significant EP test on the ground is possible
- because the signal is in the transverse plane - by exploiting the horizontal component
of the gravitational and the centrifugal field of the Earth. This ground test is underway.
. The main feature of GG is that, similarly to the most recent
ground experiments, the expected (low frequency) signal is modulated at higher frequency
by spinning the system, in this case by rotating the test bodies (in the shape of hollow
cylinders) around their symmetry axes, the signal being in the perpendicular plane. They
are mechanically suspended inside the spacecraft and have very low frequencies of natural
oscillation (due to the weakness of the springs that can be used because of
weightlessness) so as to allow self-centering of the axes; vibrational noise around the
spin/signal frequency is attenuated by means of mechanical suspensions. The signal of an
EP violation would appear at the spin frequency as a relative (differential)
displacement of the test masses perpendicularly to the spin axis, and be detected by
capacitance sensors; thermal stability across the test masses and for the required
integration time is obtained passively thanks to both the fast spin and the cylindrical
symmetry. In the nondrag-free version the entire effect of atmospheric drag is retained,
but a very accurate balancing of the test bodies must be ensured (through a coupled
suspension) so as to reach a high level of Common Mode Rejection and reduce the
differential effects of drag below the target sensitivity. In so doing the complexities of
a drag-free spacecraft are avoided by putting more stringent requirements on the
experiment. The spacecraft must have a high area-to-mass ratio in order to reduce the
effects of nongravitational forces; it is therefore a natural choice to have three pairs
of test masses (in three experimental chambers) rather than one as by Nobili et al. (1995) and the (mission called GALILEO GALILEI, 1996). The GG setup is
specifically designed for space; however, a significant EP test on the ground is possible
- because the signal is in the transverse plane - by exploiting the horizontal component
of the gravitational and the centrifugal field of the Earth. This ground test is underway.
Printable version available
(1368251 bytes)
Table of contents
- Introduction
- Experiment setup and orbit choice
- Self-centering in supercritical rotation
- Axial centering and Earth tides
- Inertial forces
- Room temperature effects
- The capacitance read out system
- Coupling to higher mass moments of the test bodies
- Electrostatic and magnetic effects
- Initial unlocking in supercritical rotation
- Conclusions
Body of article in one file
Background data sets
table1.tbl
Inertial properties of the rigid bodies constituting the FEM model

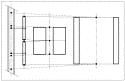
Fig. 1. Schematic section through the spin axis of the spacecraft showing the spacecraft,
the suspended laboratory and the three experimental chambers containing two test masses
each. The spacecraft is a cylinder of  height and
height and  base
diameter. The figure is to scale and shows that the experiment can be performed in a very
small and compact satellite (the area-to-mass ratio is
base
diameter. The figure is to scale and shows that the experiment can be performed in a very
small and compact satellite (the area-to-mass ratio is  . The central chamber contains two masses made of
the same (dense) material for a null test. Each of the other two chambers contains two
test masses of different materials, including low density ones. The numbers 1-8 are
referred to in Section 3 .
(to main text)
. The central chamber contains two masses made of
the same (dense) material for a null test. Each of the other two chambers contains two
test masses of different materials, including low density ones. The numbers 1-8 are
referred to in Section 3 .
(to main text)
 (72479
bytes)
(72479
bytes)
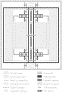
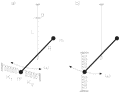
Fig. 2. Section through the spin axis of the spacecraft showing (not to scale) the
spacecraft, the PGB laboratory and (for simplicity) only one experimental chamber. The PGB
laboratory and the test masses are suspended with springs and their equilibrium positions
can be stabilized by means of electrostatic active dampers (see Fig. 19 for a top view). The suspensions of the test
masses also employ "elastic" gimbals (i.e. gimbals pivoted with torsion wires)
on two movable rods for the balancing of inertial forces discussed in Section 5.2 . The axial position of each half of these
rods can be finely adjusted by means of piezoelectric actuators (see also Fig. 13 ). The capacitive plates of the read out system,
between the test masses, are attached to inch-worms for adjusting their distance from the
surfaces of the test masses. (to main text)
 (23440
bytes)
(23440
bytes)
Fig. 3. Noise reduction factor (i.e. amplitude of disturbing vibration at the suspended
mass over amplitude of vibration at the suspension point) as function of frequency for a
suspended laboratory of  and mechanical suspensions with stiffness
and mechanical suspensions with stiffness 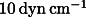 and quality factor of order 1.
and quality factor of order 1. 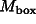 and all the rest of the
system (spacecraft plus test masses). (to main text)
and all the rest of the
system (spacecraft plus test masses). (to main text)
 (15135
bytes)
(15135
bytes)
Fig. 4. Section across the spin axes of two test bodies with their centres of mass
displaced by a distance  due to an equivalence principle violation
due to an equivalence principle violation  in the field of the Earth. For
in the field of the Earth. For 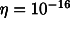 (and with mechanical
properties as given in Section 3.2 ) we get
(and with mechanical
properties as given in Section 3.2 ) we get 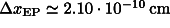 . The centres of mass of the
two bodies rotate independently around
. The centres of mass of the
two bodies rotate independently around 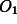 and
and  respectively. The direction of the displacement
respectively. The direction of the displacement  changes with respect to
inertial space as the satellite orbits around the Earth in
changes with respect to
inertial space as the satellite orbits around the Earth in  . (to main text)
. (to main text)
 (14013
bytes)
(14013
bytes)
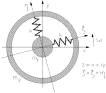
Fig. 5. A mathematical model of two axially symmetric bodies of masses  and
and 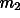 coupled by springs of
stiffness k.
coupled by springs of
stiffness k. 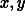 and
and 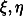 are the
inertial and the rotating plane respectively. z and
are the
inertial and the rotating plane respectively. z and  are the complex variables in the two planes. (to main text)
are the complex variables in the two planes. (to main text)
 (27477
bytes)
(27477
bytes)
Fig. 6. Sketch of the FEM (Finite Element Method) model of GG. The figure shows the final
FEM model used to analyse the rotordynamics of the active controlled system with DYNROT.
The beam elements have been drawn on the left side of the picture: the white parts
correspond to zero mass beams with structural stiffness. The nodes are shown on the right
side of the sketch, each node corresponding to two translational and two rotational
degrees of freedom which describe the lateral dynamics. In order to provide an
understandable overview each node has been located on the corresponding beam element,
instead of on the rotation axis of the satellite, as it actually is. Since each active
damper has been connected to the central rod there are shorter beam elements near the
gimbals and two nodes very close to each other. (to main
text)
 (7572
bytes)
(7572
bytes)
Fig. 7. Schematic representation of the various components of one experimental chamber
placed next to one another in order to show the different kind of connections between them
(springs, gimbals and electrostatic dampers). The outer and the inner test mass are
respectively connected by spring elements (continuous line) to the pair of movable
supports. Gimbals join the movable supports to the central rod, while the electrostatic
dampers act between the test masses and the central rod (dotted line). (to main text)
 (10470
bytes)
(10470
bytes)
Fig. 8. Mode shapes of GG satellite. The mode shapes found by the DYNROT FEM code can be
divided into three types: the first includes 7 cylindrical modes forward and backward, the
second 7 backward mainly conical modes and the third 8 conical forward modes. A sample of
each set including the  and
and 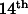 forward modes and the
forward modes and the 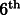 backward mode is shown by giving the
position of the axis of rotation (continuous line) and the location of the nodes (the
"
backward mode is shown by giving the
position of the axis of rotation (continuous line) and the location of the nodes (the
" " symbols). The x-
" symbols). The x- is a coordinate along the spacecraft axis
(in cm); the y-
is a coordinate along the spacecraft axis
(in cm); the y- is an
adimensional normalized coordinate (the mode automatically scales all the modes to the
maximum value). (to main text)
is an
adimensional normalized coordinate (the mode automatically scales all the modes to the
maximum value). (to main text)
 (10009
bytes)
(10009
bytes)
Fig. 9. Electrostatic damping of whirling motions. The circular instability motions of the
rotation axis of the inner shaft, which have the natural (low) frequency of the suspended
masses  , can be
actively damped by means of the electrostatic force obtained by applying a voltage pulse V
of short duration (for example for about one fourth of the spin period, i.e. about
, can be
actively damped by means of the electrostatic force obtained by applying a voltage pulse V
of short duration (for example for about one fourth of the spin period, i.e. about 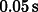 ) to each plate rotating at the (rapid) spin
frequency
) to each plate rotating at the (rapid) spin
frequency 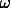 when it is passing
through the position
when it is passing
through the position 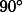 before the
point of its nearest approach to the inner shaft. This happens, for each plate, at a
frequency which is equal to the spin frequency
before the
point of its nearest approach to the inner shaft. This happens, for each plate, at a
frequency which is equal to the spin frequency 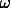 minus the natural frequency
minus the natural frequency  . (to main text)
. (to main text)
 (4236
bytes)
(4236
bytes)
Fig. 10. Simple scheme of Earth tidal forces on two test bodies which rotate around the
same axis but are displaced along it. The figure shows how the component of the tidal
force towards the Earth changes phase by  every half orbital period of the satellite around the Earth. Only this
component does produce a differential displacement of the centres of mass which can be
recorded by the spinning capacitors. It is apparent that a differential force due to a
violation of the equivalence principle would not change sign every
every half orbital period of the satellite around the Earth. Only this
component does produce a differential displacement of the centres of mass which can be
recorded by the spinning capacitors. It is apparent that a differential force due to a
violation of the equivalence principle would not change sign every 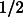 orbit and would not go to
zero with the separation distance
orbit and would not go to
zero with the separation distance 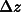 . (to main text)
. (to main text)
 (24022 bytes)
(24022 bytes)
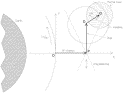
Fig. 11. Qualitative representation, in the orbital plane and for one pair of test masses,
of the differential displacements obtained from the synchronous demodulation of the
2-phase 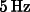 signal. The x-axis
is in the Earth-to-satellite direction and the vector
signal. The x-axis
is in the Earth-to-satellite direction and the vector  is the differential displacement, directed along the x-axis
and constant in amplitude, of the two masses due to an EP violation. The
perturbation
is the differential displacement, directed along the x-axis
and constant in amplitude, of the two masses due to an EP violation. The
perturbation 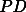 due to the initially
unbalanced atmospheric drag will be found in the area between the two dotted lines
crossing in P: the angle between them is about
due to the initially
unbalanced atmospheric drag will be found in the area between the two dotted lines
crossing in P: the angle between them is about 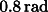 , and is due to the fact that the drag has a variable component in
the radial direction because of the solar radiation pressure (of amplitude about
, and is due to the fact that the drag has a variable component in
the radial direction because of the solar radiation pressure (of amplitude about 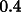 times the atmospheric drag and in the
Sun-satellite direction). Smaller contributions to the
times the atmospheric drag and in the
Sun-satellite direction). Smaller contributions to the 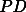 vector come from the Earth albedo, the Earth infrared radiation
and, by a smaller amount, from a possible small eccentricity of the orbit. By finely
adjusting the lengths of the suspension arms the point D is displaced up or down
inside this area, and this balancing of the drag should be continued until D is as
close as possible to P. In doing so, also the radial component is automatically
balanced. The resonant variations of the drag (not shown) will oscillate inside the same
area. The vector
vector come from the Earth albedo, the Earth infrared radiation
and, by a smaller amount, from a possible small eccentricity of the orbit. By finely
adjusting the lengths of the suspension arms the point D is displaced up or down
inside this area, and this balancing of the drag should be continued until D is as
close as possible to P. In doing so, also the radial component is automatically
balanced. The resonant variations of the drag (not shown) will oscillate inside the same
area. The vector  is
the instability due to the internal dissipation of the springs (Section 3.2 ), slowly rotating and increasing: it must be
actively damped until Q is as close as possible to D (and P). The
circle around point Q represents the error in the measurement due to the thermal
noise of the mechanical oscillations in a few days of integration time. The actual values
of all these quantities are discussed in the text. (to main
text)
is
the instability due to the internal dissipation of the springs (Section 3.2 ), slowly rotating and increasing: it must be
actively damped until Q is as close as possible to D (and P). The
circle around point Q represents the error in the measurement due to the thermal
noise of the mechanical oscillations in a few days of integration time. The actual values
of all these quantities are discussed in the text. (to main
text)
 (4955
bytes)
(4955
bytes)
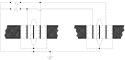
Fig. 12. Testing of suspension springs. By means of a torsion pendulum one can make ground
tests of the longitudinal (a) and of the transversal (b) characteristics of the very thin
and weak springs that will be used in orbit at zero g. One can test one spring at a
time or, as shown in this figure, measure the differences between two of them. (to main text)
 (12319 bytes)
(12319 bytes)
Fig. 13. The system of piezoelectric actuators placed in the two balancing rods. The  and
and  signs represent the intrinsic polarization of the actuators, i.e.
how each one of them must be oriented when mounted. Control voltages are applied to the
actuators (when they are applied with the opposite polarity they should not exceed a
certain value, which however is relatively high, so as not to risk to depolarize the
piezoelectrics): the sum
signs represent the intrinsic polarization of the actuators, i.e.
how each one of them must be oriented when mounted. Control voltages are applied to the
actuators (when they are applied with the opposite polarity they should not exceed a
certain value, which however is relatively high, so as not to risk to depolarize the
piezoelectrics): the sum  determines the relative axial position of the barycentres of the test masses
and is used for axial centering (Section 4 ). The
voltage difference
determines the relative axial position of the barycentres of the test masses
and is used for axial centering (Section 4 ). The
voltage difference  can be used to change the lengths of the four halves of the rods so as to balance out the
effect of transverse inertial forces (in particular the along-track component of the air
drag). (to main text)
can be used to change the lengths of the four halves of the rods so as to balance out the
effect of transverse inertial forces (in particular the along-track component of the air
drag). (to main text)
 (6105
bytes)
(6105
bytes)
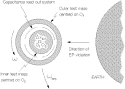
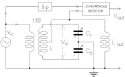
Fig. 14. Outline of the read-out circuit. The two variable capacitors  and
and  and the two halves of the
inductor L form an LC bridge whose output is proportional to the difference between
the two capacitances. (to main text)
and the two halves of the
inductor L form an LC bridge whose output is proportional to the difference between
the two capacitances. (to main text)
 (13458
bytes)
(13458
bytes)
Fig. 15. Each capacitor of the read-out system (see also Fig.
16 ) is formed by two surfaces, one for each of the two grounded masses, and one
plate, to which a sinusoidal voltage is applied. Any differential displacement of the test
masses with respect to the plates causes a loss of balance of the system and therefore an
output signal. (to main text)
 (9329
bytes)
(9329
bytes)
Fig. 16. The surfaces of the capacitors before and after: a) a common mode displacement
and b) a differential mode displacement. (to main text)
 (17670 bytes)
(17670 bytes)
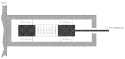
Fig. 17. Scheme of the inch-worm. Lateral piezoelectric actuators alternately fasten and
release the extremities of the inch-worm to the sides of its container while the inner
part is made to expand and contract by means of the other piezoelectrics. In this way the
inch-worm can move on a relatively long path in successive very small steps. (to main text)
 (6296
bytes)
(6296
bytes)
Fig. 18. In an equatorial orbit the direction of the Earth's magnetic field is not more
than about  away from the
perpendicular to the orbit. Therefore its effects in the plane of the orbit will be
reduced to about
away from the
perpendicular to the orbit. Therefore its effects in the plane of the orbit will be
reduced to about  times those of
the full field. These effects are distinguishable from a violation of the equivalence
principle because they change sign every half orbit. (to
main text)
times those of
the full field. These effects are distinguishable from a violation of the equivalence
principle because they change sign every half orbit. (to
main text)
 (47160
bytes)
(47160
bytes)
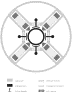
Fig. 19. Top view of a set of four inch-worms actuators for locking and unlocking the
suspended masses. Each mass needs two such sets placed at its two axial ends (see also Fig. 2 ). Between the inch-worms are the electrostatic
plates used for active damping. The rod, hence the suspended masses, is locked during
launch and until the spacecraft has reached the final spin angular velocity 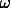 . Then the inch-worms equipped with pressure
sensors sensitive to
. Then the inch-worms equipped with pressure
sensors sensitive to 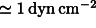 are used for initial centering until the centrifugal forces detected by the pressure
sensors become smaller than the forces that can be generated by the electrostatic plates.
At this point the inch-worm will be retracted and the electrostatic system will complete
the centering and will keep it stable. (to main text)
are used for initial centering until the centrifugal forces detected by the pressure
sensors become smaller than the forces that can be generated by the electrostatic plates.
At this point the inch-worm will be retracted and the electrostatic system will complete
the centering and will keep it stable. (to main text)
References
- Adelberger, E.G., Stubbs, C.W., Heckel, B.R., Su, Y., Swanson, H.E., Smith, G.,
Gundlach, J.H., & Rogers, W.F., 1990, PhRvD, 42, 3267.
- Barlier, F., Blaser, J.P., Cavallo, G., et al., 1991, in: STEP: Satellite Test of the
Equivalence Principle, Assessment Study Report, ESA/NASA SCI (91) 4.
- Bender, P., Brillet, A., Ciufolini, I., Danzmann, K., Hellings, R., Hough, J., Lobo, A.,
Sandford, M., Schutz, B., & Touboul, P., 1994, in: LISA: Laser Interferometer Space
Antenna for gravitational waves measurements, ESA SCI (94) 5.
- Beverini, N., Billen, J.H., Bonner, B.E., et al., 1986, CERN/PSCC/86-2 PSSC/P-64, Los
Alamos National Laboratory Report LA-UR-86-260.
- Blaser, J.P., Bye, M., Cavallo, G., et al., 1993, STEP: Satellite Test of the
Equivalence Principle, Report on the Phase Study, A, ESA/NASA SCI (93) 4.
- Blaser, J.P., Cruise, M., Damour, T., Leňn, J., Paik, H.J., & Rummel, R., 1994,
STEP: Satellite Test of the Equivalence Principle. A Fundamental Physics Laboratory in
Space, Assessment Study Report, ESA SCI (94) 5.
- Blaser, J.P., Cornelisse, J., Cruise, et al., 1996, STEP: Satellite Test of the
Equivalence Principle, Report on the Phase Study, A, ESA SCI (96) 5.
- Braginsky, V.B., private communication, 1993.
- Braginsky, V.B. & Panov, V.I., 1972, Sov. Phys. JEPT 34, 463.
- Bramanti, D., Nobili, A.M., & Catastini, G., 1992, Phys. Lett. A 164, 243.
- Bramanti, D., Nobili,
A.M., & Catastini, G., 1996, Stabilization of Weakly Coupled Rotors: A General
Derivation of the Required Forces.
- Cajori, F., 1934, Sir Isaac Newton's Mathematical Principles of Natural Philosophy and
his System of the World (University of California, Berkeley, CA).
- Cappellari, J.O., et al., 1976, Mathematical Theory of the Goddard Trajectory
Determination System, GSFC X-582-76-77, Sections 4.5.6, 4.53-4.57.
- Catastini, G., Bramanti, D., Nobili, A.M., Fuligni, F., & Iafolla, V., 1992, ESA
Journal 16, 401.
- Catastini, G., Nobili,
A.M., & Bramanti, D., 1996, Passive Vibration Isolation in a Spinning Spacecraft.
- Chapman, P.K. & Hanson, A.J., 1970, Proceedings of the Conference on Experimental
Tests of Gravitational Theories, Cal. Tech. JPL TM No. 33-499, p. 228.
- Den Hartog, J.P., 1985, Mechanical Vibrations (Dover Publications, Inc., New York, first
published 1934).
- Ducarme, B., 1994, private communication.
- Eötvös, R.V., Pekar, D., & Fekete, E., 1922, Ann. Physik 68, 11.
- Fishbach, E., Sudarsky, D., Szafer, A., Talmadge, C., & Aronson, S.H., 1986, Phys.
Rev. Lett., 56, 3.
- Galilei, G., 1638, Discorsi e Dimostrazioni Matematiche intorno a due Nuove Scienze
Attinenti alla Meccanica e i Movimenti Locali, in: Barbčra G., eds. (Le Opere, Firenze,
VIII., 1968) p. 116.
- GALILEO GALILEI (GG), PRE PHASE A REPORT, ASI (Agenzia Spaziale Italiana, September
1996).
- GALILEO GALILEI
(GG), ADDENDUM No. 1 TO THE PRE PHASE A REPORT, ASI(Agenzia Spaziale Italiana, May 1997).
- Genta, G., 1993, Vibration of structures and machines (Springer, New York).
- Harris, I. & Priester, W., 1952, Jour. Atmos. Sciences, 19, 4 (also NASA-TN-D-1443).
- Harris, I. & Priester, W., 1962, Theoretical Models for the Solar Cycle Variation of
the Upper Atmosphere, in: GSFC Report NASA-TN-D-144.
- Haselden, G.G., ed., 1971, Cryogenic Fundamentals (Academic Press, London).
- Immergut, B., ed., 1984, Polymer Handbook 2
 Ed. (J. Wiley & Sons, New York).
Ed. (J. Wiley & Sons, New York).
- Jacchia, L.G., 1971, Revised Static Models of the Termosphere and Exosphere with
Empirical Temperature Profiles, in: SAO Special Report No. 332 (Cambridge, MA).
- Jeffcott, H.H., 1919, Philos. Mag. Series 6, 37, 34.
- Melchior, P., 1978, The Tides of the Planet Earth (Pergamon, Oxford).
- Melchior, P., Barlow, B., Ducarme, B., & Delcourt, M., 1979, Discussion of a Long
Series of Gravity Tide Measurements at Alice Springs in the Centre Australia, in: IUGG
Gen. Assembly, Symp. 20 (Canberra, ACT).
- Milani, A., Nobili, A.M., & Farinella, P., 1987, Non-Gravitational Perturbation and
Satellite Geodesy (Adam Hilger, Bristol).
- Nobili, A.M., Milani, A., Polacco, E., Roxburgh, I.W., Barlier, F., Aksnes, K., Everitt,
C.W., Farinella, P., Anselmo, L., & Boudon, Y., 1990, ESA Journal, 14, 398.
- Nobili, A.M., Catastini, G., Di Virgilio, A., Iafolla, V., & Fuligni, F., 1991,
Phys. Lett. A, 160, 45.
- Nobili, A.M., Bramanti, D.,
Polacco, E., et al., 1994, Proposed New Test of the Equivalence Principle in Space, PISA
Preprint on Astrophysics and Space Mechanics (Revised February 1995).
- Nobili, A.M., Bramanti, D., Catastini, G., et al., 1995, J. Astronautical Sciences, 43,
219.
- Nobili, A.M., Bramanti, D., Catastini, G., Anselmi, A., Portigliotti, S., Lenti, A.,
Volpi, G., & Marcuccio, S., 1996, Galileo Galilei (GG) - Test of the Equivalence
Principle with a small Spinning satellite: The Stabilization of its Weakly Coupled Masses,
in: Scientific Satellites Achievements and Prospects in Europe, Proceedings AAAF-ESA 3.74.
- Park, J.W., 1990, PhD Thesis (University of Maryland).
- Quinn, T.J., 1993, private communication.
- Roberts, Jr., E.R., 1971, Celest. Mech. 4 (3/4), 368.
- Roll, P.G., Krotkov, R., & Dicke, R.H., 1964, Ann. Phys. (NY) 26, 442.
- Sanders, A.J. & Deeds, W.E., 1992, PhRvD, 46, 489.
- Scherk, J., 1979, Phys. Lett. B 88, 265.
- Su, Y., 1992, PhD Thesis (University of Washington).
- Su, Y., Heckel, B.R., Adelberger, E.G., Gundlach, J.H., Harris, M., Smith, G.L., &
Swanson, H.E., 1994, PhRvD, 50, 3614.
- Whitley, S., 1984, Rev. Mod. Phys., 56, 67.
- Will, C.M., 1992, Int. J. Mod. Phys. D, 1, 13.
- Worden, Jr., P.W., 1976, PhD thesis (Stanford University).
- Worden, Jr., P.W., 1987, Acta Astronautica, 5, 27.
- Worden, Jr., P.W. & Everitt, C.W.F., 1973, Proceedings Int. School of Physics E.
Fermi, Course LVI: Experimental Gravitation (Academic Press, New York), p. 381.
- Worden, Jr., P.W., Everitt, C.W.F., & Bye, M., 1990, Satellite Test of the
Equivalence Principle, Science Requirements Document (Stanford University).
Copyright © 1998 Elsevier Science B.V., Amsterdam. All Rights Reserved.



(Anna Nobili- nobili@dm.unipi.it)
Last edited May 14, 1998
![]() and the inertial mass
and the inertial mass ![]() are always in the same positive ratio in all test bodies. A space
experiment offers two main advantages: a signal about a factor of a thousand bigger than
on Earth and the absence of weight. A new space mission named GALILEO GALILEI (GG) has
been proposed (Nobili et al., 1995; GALILEO GALILEI, 1996) aimed at testing the
weak Equivalence Principle (EP) to 1 part in
are always in the same positive ratio in all test bodies. A space
experiment offers two main advantages: a signal about a factor of a thousand bigger than
on Earth and the absence of weight. A new space mission named GALILEO GALILEI (GG) has
been proposed (Nobili et al., 1995; GALILEO GALILEI, 1996) aimed at testing the
weak Equivalence Principle (EP) to 1 part in ![]() in a rapidly spinning (
in a rapidly spinning (![]() )
drag-free spacecraft at room temperature, the most recent ground experiments having
reached the level of
)
drag-free spacecraft at room temperature, the most recent ground experiments having
reached the level of ![]() (Adelberger et al., 1990; Su et al., 1994). Here we present a nondrag-free
version of GG which could reach a sensitivity of 1 part in
(Adelberger et al., 1990; Su et al., 1994). Here we present a nondrag-free
version of GG which could reach a sensitivity of 1 part in ![]() . The main feature of GG is that, similarly to the most recent
ground experiments, the expected (low frequency) signal is modulated at higher frequency
by spinning the system, in this case by rotating the test bodies (in the shape of hollow
cylinders) around their symmetry axes, the signal being in the perpendicular plane. They
are mechanically suspended inside the spacecraft and have very low frequencies of natural
oscillation (due to the weakness of the springs that can be used because of
weightlessness) so as to allow self-centering of the axes; vibrational noise around the
spin/signal frequency is attenuated by means of mechanical suspensions. The signal of an
EP violation would appear at the spin frequency as a relative (differential)
displacement of the test masses perpendicularly to the spin axis, and be detected by
capacitance sensors; thermal stability across the test masses and for the required
integration time is obtained passively thanks to both the fast spin and the cylindrical
symmetry. In the nondrag-free version the entire effect of atmospheric drag is retained,
but a very accurate balancing of the test bodies must be ensured (through a coupled
suspension) so as to reach a high level of Common Mode Rejection and reduce the
differential effects of drag below the target sensitivity. In so doing the complexities of
a drag-free spacecraft are avoided by putting more stringent requirements on the
experiment. The spacecraft must have a high area-to-mass ratio in order to reduce the
effects of nongravitational forces; it is therefore a natural choice to have three pairs
of test masses (in three experimental chambers) rather than one as by Nobili et al. (1995) and the (mission called GALILEO GALILEI, 1996). The GG setup is
specifically designed for space; however, a significant EP test on the ground is possible
- because the signal is in the transverse plane - by exploiting the horizontal component
of the gravitational and the centrifugal field of the Earth. This ground test is underway.
. The main feature of GG is that, similarly to the most recent
ground experiments, the expected (low frequency) signal is modulated at higher frequency
by spinning the system, in this case by rotating the test bodies (in the shape of hollow
cylinders) around their symmetry axes, the signal being in the perpendicular plane. They
are mechanically suspended inside the spacecraft and have very low frequencies of natural
oscillation (due to the weakness of the springs that can be used because of
weightlessness) so as to allow self-centering of the axes; vibrational noise around the
spin/signal frequency is attenuated by means of mechanical suspensions. The signal of an
EP violation would appear at the spin frequency as a relative (differential)
displacement of the test masses perpendicularly to the spin axis, and be detected by
capacitance sensors; thermal stability across the test masses and for the required
integration time is obtained passively thanks to both the fast spin and the cylindrical
symmetry. In the nondrag-free version the entire effect of atmospheric drag is retained,
but a very accurate balancing of the test bodies must be ensured (through a coupled
suspension) so as to reach a high level of Common Mode Rejection and reduce the
differential effects of drag below the target sensitivity. In so doing the complexities of
a drag-free spacecraft are avoided by putting more stringent requirements on the
experiment. The spacecraft must have a high area-to-mass ratio in order to reduce the
effects of nongravitational forces; it is therefore a natural choice to have three pairs
of test masses (in three experimental chambers) rather than one as by Nobili et al. (1995) and the (mission called GALILEO GALILEI, 1996). The GG setup is
specifically designed for space; however, a significant EP test on the ground is possible
- because the signal is in the transverse plane - by exploiting the horizontal component
of the gravitational and the centrifugal field of the Earth. This ground test is underway.

 (72479
bytes)
(72479
bytes)  (23440
bytes)
(23440
bytes)  (15135
bytes)
(15135
bytes)  (14013
bytes)
(14013
bytes)  (27477
bytes)
(27477
bytes)  (7572
bytes)
(7572
bytes)  (10470
bytes)
(10470
bytes)  (10009
bytes)
(10009
bytes)  (4236
bytes)
(4236
bytes)  (24022 bytes)
(24022 bytes)  (4955
bytes)
(4955
bytes)  (12319 bytes)
(12319 bytes)  (6105
bytes)
(6105
bytes)  (13458
bytes)
(13458
bytes)  (9329
bytes)
(9329
bytes)  (17670 bytes)
(17670 bytes)  (6296
bytes)
(6296
bytes)  (47160
bytes)
(47160
bytes) ![]()
![]()
![]()