Comparison with the ESTEC Result

In none of these two different derivations we recover the result reported in the Appendix to the ESTEC Technical Assessment of GG (as released on October 7, 1996), namely:

The ESTEC Appendix contains in fact an incorrect definition of the non-rotating damping forces which are needed to stabilize the whirling motions. On page 16 (lines 18-20) one can read: ``... non-rotating damping forces are obtained by virtue of the naturally unavoidable viscous friction between the rotating body and the non-rotating parts, ...". This is in fact the definition of the friction in the bearings, which is not the non-rotating damping needed for stabilization (see below; see also the GG Blue preprint, §III). Also incorrect are the definitions, given on page 41 (beginning of Section 2.1) for the rotating and non-rotating damping. It is stated: ``Consider the general case where represents the viscous damping coefficient in the rotating frame, and represents the viscous damping coefficient in the inertial frame (`non-rotating damping')''. The damping coefficients derive from physical friction, hence from dissipated energy, which do not depend on the reference system from where they are looked at. The physical dimension of damping coefficients is mass/time, which in Galilean mechanics does not depend on the reference frame. The ``rotating damping'' and the ``non-rotating damping'' are not the same effect as seen from different reference frames: they are the names of two different types of damping in the same reference frame. They have different physical properties (respectively in destabilizing and in stabilizing the rotor) that do not depend on the reference frame. Moreover, as we have just said above, they have nothing to do with a third type of damping: the viscous friction in the bearings.

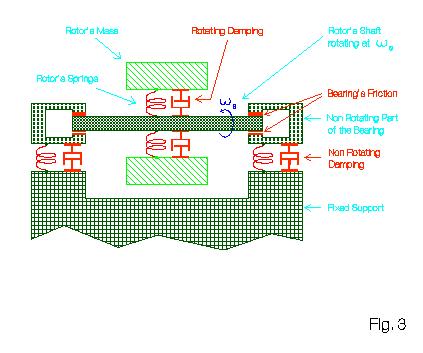
Figure 3: Rotating machine with rotating damping, non-rotating damping and friction in the bearings.

In Fig. 3 we show the three general types of friction in a rotating machine, from which the correct definition of rotating and non-rotating damping is obtained. They are:

1. The friction in the bearings. This is the friction (mostly viscous) between the rotating body and the non rotating parts, which is obviously effective in slowing down the rotor but almost completely ineffective at damping whirling motions (and also at producing them). An important advantage of the GG space experiment is the absence of bearings, hence of bearings friction at all (and we certainly don't want to simulate them actively!).
2. The rotating damping friction. This is the friction (viscous plus structural) between two parts of the system which are both rotating (i.e. two parts of the rotor). The corresponding losses are those which produce the instabilities (whirling motions) in weakly suspended rotors with by giving rise to the destabilizing forces computed above (namely of the spring elastic forces). In the GG space experiment where all rotors are suspended with tiny springs in vacuum the rotating damping friction is essentially structural, caused by the relative motion of the various parts of the springs subject to mechanical deformations (at spin minus natural frequency, which is essentially the spin frequency). Adding the rotating friction generated by the rotating electrostatic active dampers themselves, which provide a force much smaller than the spring force, does in no way change the dynamics of the GG system.
3. The non-rotating damping friction which generates the non-rotating damping forces. This is the friction (viscous plus structural) between two parts of the system both non-rotating (i.e. between two parts of the non-rotating supports, for example the friction between the non-rotating part of the bearings and their fixed supports). The non-rotating damping forces are effective in damping transverse translational oscillations of the rotor's axis of rotation (for example the whirling motions), and they can do this without slowing down its rotation. For the whirling motions to be stabilized they must simply provide a coefficient of non-rotating damping which satisfies the inequality (55). For instance, in the ground rotors in which non-rotating damping is provided by tipping the non-rotating part of the bearing in oil this is essentially viscous damping. In the GG space experiment where there are no non-rotating parts an equivalent non-rotating damping is provided by electrostatic actuators fixed in the rotating system. (see §4)

From a physical viewpoint the most important characteristic distinguishing the effects of rotating and non-rotating damping on one side from the effects of friction in the bearings on the other is that the former produce forces on the rotor, while the latter produces torques. They are therefore independent from one another and interact only to a second order, namely because of construction errors, asymmetries, misalignements etc. From this it follows that if one were in fact using the forces generated by the friction in the bearings in order to stabilize the whirling motions (rather than the forces due to non rotating damping), he would inevitably need extremely large forces.

As for the amplifying factor claimed in the ESTEC Appendix as due to the fact that the active dampers are fixed to the rotating bodies, we have shown in §4 above that there is no physical grounds for it. So, the results of the ESTEC Appendix are based on the use of supposedly ``stabilizing'' forces which are a factor larger than we have shown (both theoretically and with numerical simulations) to be sufficient for damping the GG whirling motions. Let us see what is the effect of the huge ESTEC ``stabilizing'' force when applied to one of the masses m undergoing a destabilizing forward whirling motion at frequency (as demonstrated by Eqs. (11) to (14) for all cases except the one of very high viscous damping, which can be ruled out in GG) at distance from the equilibrium position. Since the ESTEC ``stabilizing'' force amounts to it is apparent that it is compatible with two effects. In one case it could force the body to whirl at angular velocity , much larger than its previous angular velocity of whirl when the system was undamped, at a distance from the equilibrium position, or, it could maintain the angular velocity of whirl of the undamped situation while pushing the body a distance away from the equilibrium position. If and Q is rather small (e.g. 20 for the PGB and 500 for the test masses), then it is apparent that in either case the huge ESTEC force, far from damping the whirling motions would force the two masses into a totally wrong dynamical configuration overcoming the spring forces and thus disrupting the whole experiment.

Research Papers Available Online

       (Anna Nobili- nobili@dm.unipi.it)