Consider the rotor of Fig. 1. The relative motion of the two masses is described (in the inertial reference frame) by the equation:
where z is the position vector in the complex plane, 
is the reduced mass of the
system, 
is the coefficient of rotating damping and there is no non-rotating
damping (see §6). The characteristic equation associated to the equation of motion of the
system is:
The solution of Eq. (A2) is of the type 
, so that the real part of
, 
, is the angular frequency of the whirling motion when the imaginary
part of is negative. Therefore the destabilizing forward whirling motion has
frequency:
Let us compute for a system dominated by structural
damping and for a system dominated by viscous damping.
is written as: 
hence:
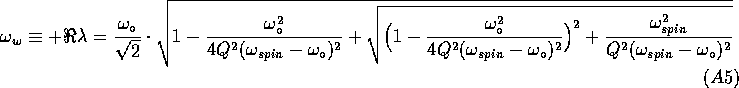
and, if 
:
Since rotating damping derives from dissipation at frequency 
, the
corresponding Q is certainly such that 
, yielding:
is written as: 
with 
the quality factor of the system due to rotating friction of viscous
nature. Then:
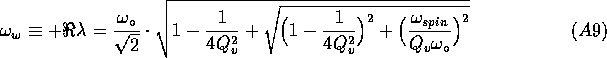
Since and 
, the quantity 
is dominant
with respect to 
and we have:
It follows that the whirling frequency is:
The case of very large viscous damping can certainly be ruled out in GG (and probably
also in ground rotating machines with 
). This means that in GG the coefficient
of viscous rotating damping (A8) can never be used with a value of such that 
. We
shall have 
( 
) with 
in the case of small
viscous friction, and 
in the intermediate case. Hence, 
where Q is the quality factor due to structural damping. This means 
in the case of
small viscous friction and 
in the intermediate case. The force
required to stabilize the whirling motion is in all cases smaller than the elastic force
of the spring (Eqs. (37), (39)). In GG, rotating friction comes from dissipation, in
vacuum and at the spin frequency, in the tiny suspension springs and in the small rotating
electrostatic plates which provide stabilizing forces much smaller than the spring forces
themselves (see §4). Therefore, rotating structural friction is bound to be very small
and rotating viscous friction (e.g. due to imperfect clamping of the suspensions) very
small, if any. Ground tests based on the measurement of 
, 
and 
will be performed
to determine the nature of rotating damping in the system using the results (A7)
and (A11).
(Anna Nobili- nobili@dm.unipi.it)
)
