GALILEO GALILEI" (GG)
A Small Satellite to Test the
Equivalence Principle of Galileo, Newton and Einstein
Proposal to ESA, F2&F3 Competition, January 31 2000
2. Main Features and Novelties of the GG Space Experiment
In this chapter we briefly describe the main features of the GG space experiment and mission, outline the main differences with respect to STEP20,21,22,1,2, and describe the major advantages we see in the GG design. Details on GG are available in the literature23,24,25; the most complete analysis so far is given in the ASI Report on GG Phase A Study26.
2.1 High Frequency Modulation of the Expected SignalThe advantage of a space experiment for EP testing (with a much stronger signal) was recognized soon after the beginning of the space age. While designing a space experiment scientists also tried to provide high frequency modulation. The first proposed fast rotating experiment27, in 1970, envisaged a fast rotating platform so as to modulate the signal at its rotating speed. Unfortunately, in this apparatus the test bodies were constrained along one diameter of the rotating platform, and it is well known that any such unidimensional rotating system is always strongly unstable above the critical speed28, Ch. 6.1. The experiment concept was therefore incorrect, as long as high frequency modulation was the issue. Freedom to move in a plane (as it is the case for the GG test bodies) would solve this problem.
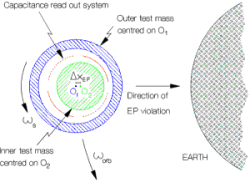
Figure 2.1 shows, in the plane perpendicular to the spin/symmetry axis, how the GG coaxial test cylinders (of different composition) would move one with respect to the other were they attracted differently by the Earth because of an EP violation. The Figure shows the test cylinders one inside the other and two pairs (for doubling the output data) of capacitance plates in between them to measure any relative displacement. If one of the bodies is attracted by the Earth more than the other, the two centers of mass move away from one another always towards the center of the Earth. In GG the test cylinders are coupled by very weak mechanical suspensions so that even a tiny differential force (in the plane perpendicular to the spin/symmetry axis) causes a mechanical displacement which is detectable once transformed into an electric potential signal by the capacitance read-out. The weaker the coupling, the longer the natural period of differential oscillations of the test bodies, the more sensitive the system is to differential forces such as the one caused by an EP violation.
Figure
2.1. Section of the GG coaxial test
cylinders and capacitance sensors in the plane perpendicular to the spin axis (not to
scale). The capacitance plates of the read-out are shown in between the test bodies, in
the case in which the centers of mass of the test bodies are displaced from one another by
a vector 
due to an Equivalence Principle violation in the
gravitational field of the Earth (e.g., the inner test body is attracted by the Earth more
than the outer one because of its different composition). Under the (differential) effect
of this new force the test masses, which are weakly coupled by mechanical suspensions,
reach equilibrium at a displaced position where the new force is balanced by the weak
restoring force of the suspension, while the bodies rotate independently around O1
and O2 respectively (see plot of simulation in26, Fig. 6.4) .
The vector of this relative displacement has constant amplitude (for zero orbital
eccentricity) and points to the center of the Earth (the source mass of the gravitational
field); it is therefore modulated by the capacitors at their spinning frequency with
respect to the center of the Earth.
In the current settings and full simulation of GG at Phase A level26 the natural period for differential
oscillations of the test bodies is about 545sec: an EP violation by only 1 part in 1017
would cause, in this system, a displacement of the test cylinders by about 6× 10-11cm, which can be detected as a voltage signal of
about 1nV with a capacitance read-out which has already been manufactured and
tested in the laboratorySec. 5. It is apparent
from Figure 2.1 that spinning capacitance plates modulate the amplitude of the displacement caused by an EP violation at their
spinning frequency with respect to the Earth (2Hz in the current baseline), with a well
defined phase (the vector does always point towards the center of the Earth). In absence
of spin the signal has constant intensity (except for the effect of the orbital
eccentricity of the satellite, which is close to zero: e<0.01) and a direction changing
at the orbital frequency of the satellite around the Earth (@
1.75× 10-4 Hz); so in GG the signal is modulated at
a frequency about 104 times higher than the frequency of the signal, the
advantage being the reduction of low frequency electronic and mechanical noise. The
spinning state of the GG spacecraft is a stable 1-axis rotation and needs no active
control.
In STEP20,21,22,1,2 (Figure 2.2) the concentric test cylinders must be kept fixed with respect to inertial space by active control of the spacecraft, their symmetry axis is the sensitive axis and lies in the orbital plane (the system is very stiff in the plane perpendicular to the symmetry axis). If the cylinders are attracted differently by the Earth because of an EP violation there is a relative movement of the two one inside the other; the effect is maximum when the symmetry axis is directed towards the center of the Earth (changing sign as the satellite moves by 180° around the Earth) and it is zero when the symmetry axis is perpendicular to the satellite-to-Earth direction. Hence, the signal has an intensity varying at the orbital frequency of the satellite. Any higher frequency signature, higher than the orbital frequency, that one would wish to impress on the signal requires the spacecraft to be spun around its actively controlled space-fixed attitude. Due to the STEP design these can only be slow rotations (hence yielding only low frequency modulation) which in addition require a careful and accurate active control..
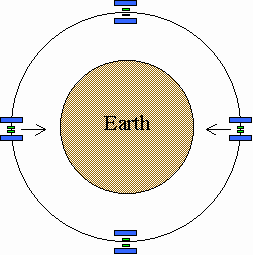
Figure 2.2 Schematic view of the STEP test cylinders as they orbit around the Earth. The sensitive axis is the symmetry axis of the cylinders which, together with the spacecraft (not shown), are kept fixed with respect to inertial space by active control. A differential attraction from the Earth due to a violation of the Equivalence Principle would give a signal with the same period as the orbital period of the satellite (@ 6000 sec).
2.2 Room Temperature vs Cryogenics: Advantages of the GG Design at Room Temperature and for a More Accurate Cryogenic Mission in the Future
A very important consequence of the fact that in GG the expected signal lies in the plane normal to the spin/symmetry axis of the test cylinders is that a major perturbation due to the so called radiometer effect is zero also at room temperature29. It is known that, in low pressure conditions where the mean free path of the gas particles is much larger than the dimensions of the vessel, a cylinder whose faces are not at the same temperature is subject to an acceleration along its symmetry axis whose value is exceedingly large unless the residual gas pressure is extremely low, down to values which can only be obtained at extremely low temperature close to absolute zero.
In STEP the radiometer effect along the symmetry/sensitive axis of the test cylinders competes directly with the signal, and is reduced thanks to the extremely low level of residual pressure (and to a millikelvin requirement on temperature gradients), which can be obtained by operating at superfluid He temperature. Instead, a hollow cylinder whose inner and outer surfaces were not exactly at the same temperature, would have zero radiometer effect in the plane perpendicular to its axis, for pure symmetry reasons. In reality, azimuthal asymmetries as well as the radiometer effect along the symmetry axis of the cylinders must be taken into account in GG, since it is a non cryogenic experiment; however, the requirements they impose on the amount of acceptable temperature gradients are compatible with a pure passive thermal control of the GG experimental apparatus29. This eliminates one of the main reasons why a high accuracy EP experiment in space should be operated in cryogenic conditions.
Low temperature is certainly helpful in reducing thermal noise. However, it is worth recalling that thermal noise acceleration depends not only on the experiment temperature T, but also on the mass M of the test bodies according to: µ (T/M)1/2. Therefore, in GG we use more massive test bodies than in STEP in order to compensate for the higher temperature: test masses of 10kg each at 300K, as we have, result in the same thermal noise acceleration as with test masses of 0.1kg at a temperature of 3K, as in STEP.
Nevertheless, in order to reduce thermal noise even further by also decreasing the temperature, a future, lower temperature version of the GG experiment can be envisaged for which the rapid spin gives a very important advantage: the very high centrifugal force at the periphery of the spacecraft would dominate the motion of the refrigerating (movable) material and largely reduce, by symmetry, its perturbations on the experiment core; evaporation can take place along the spin axis for symmetry reasons too. Non-spinning or slowly spinning satellite experiments for EP testing do not have this property, and in fact perturbations from the nearby refrigerant mass (a few hundred liters of He in the case of STEP) are known to be a serious source of perturbation which has to be taken care of1,2.
As for the read-out, capacitance sensors at room temperature are proved to be adequate to the task (the expected bridge unbalance electric signal is of about 1nV; seeSec. 5) thus indicating no need for a low temperature measurement device.
2.3 Weak Mechanical Coupling of the Test Bodies and Passive Electric Discharging
Inside the GG spacecraft (Figures 2.3 and 2.4) there are no free-floating masses: the test bodies are mechanically suspended from an intermediate laboratory (the so called PGB, Pico Gravity Box), in its turn weakly suspended from the spacecraft (for vibration isolation), in a nested configuration of cylindrical symmetry. In this way the suspensions can provide electric grounding of the test bodies and no active discharging device is needed (which would also require to measure the exact amount of the acquired charge by somehow acting on the test bodies themselves). Passive electric discharging is a major advantage because the electric forces caused by even a very limited amount of charge (in the Van Allen belts and South Atlantic Anomaly) are enormous compared to the extremely small gravitational force to be detected.
A comparison with STEP makes it apparent how serious charging problems can be. In STEP as studied by ESA at Phase A level2 for the M3 competition (with a target in EP testing of 1 part in 1017 like GG), a 2-cm thick tungsten shield (weighing @ 130kg) was considered as baseline in order to have a time span of a few days available before discharging was needed again2, Mission Summary and Sec. 3.6.1. In the previous Phase A Study of STEP carried out by ESA for the M2 competition in collaboration with NASA (same target in EP testing) the problem had already been recognized as a serious one, although the baseline solution was different: it was decided to add a radiation sensor on board so as to be able to discard the contaminated data1, Sec. 3.4.4. In addition, it must be noted that in STEP charged particles affect the EP experiment also by asymmetrical momentum transfer along the sensitive axis of the test bodies, especially because their masses are small (a few hundred grams)1, Sec. 3.4.3. It is therefore a very good feature of GG to be essentially unaffected by Van Allen belt effects and electrostatic charging.
In point of fact, if we look at the history of small force gravitational experiments for EP testing, as well as for measuring the universal constant of gravity G (an experiment even more difficult than EP testing!), there is no question that ever since the work of Henry Cavendish at the end of the 18th century till the sophisticated experiments of more recent years, the best results have been obtained with an apparatus (the torsion balance, in different variants) where the suspension is mechanical and the test bodies are not acted upon by any active device. In STEP and in similar proposed experiments the test bodies are not suspended mechanically, but this does not mean that they are free floating: they are coupled with a low stiffness (but non zero!) elastic constant which however does not provide electric discharging as a very thin mechanical suspension (possible in space thanks to weightlessness) would do.
The weak mechanical coupling of the GG test bodies, obtained by means of helical springs (Figure 2.5) and flat gimbals (Figure 2.6) pivoted on thin torsion wires, is the key feature which allows GG to cope with a major dangerous effect: that of air drag along the satellite orbit. Air resistance acting on the spacecraft surface is experienced by the test bodies suspended inside it as a translation inertial acceleration equal and opposite to the one caused by air drag on the center of mass of the whole satellite (spin axes are stable due to the extremely high energy of spin). This acceleration is about 8 orders of magnitude weaker than 1-g on Earth, but about as many orders of magnitude larger than the expected signal; it should be the same on both test cylinders, but only in the ideal case that their masses and suspensions were exactly the same.
Figure 2.4. Section through the spin axis of the GG satellite. The solar panels are shown, in two cylindrical halves at the two ends of a girdle. Inside the spacecraft is shown the PGB laboratory with its helical suspension springs..
Figure 2.5. One helical spring, to be used for suspending the GG test bodies, clamped and ready for measuring its quality factor at a frequency of a few Hz (in vacuum). A small mass is attached to the free end of the spring in order to obtain the desired oscillation frequency. Note that the measurement is done for horizontal oscillations for the result not to be affected by local gravity. The spring has been manufactured by electroerosion in 3D from a single piece of CuBe with special equipment; Brush-Wellman heat treatment and ultrasound cleaning have been applied. The elastic properties are close to the desired ones. The best measured value for its quality factor (at 5 Hz) was 19,000. Two springs are needed for each test body (Figure 3.2). Each spring is clamped by the thick rings at its ends. Note that half turns of the springs are clockwise and the other half counter- clockwise, for de-coupling torsional from longitudinal (axial) oscillations. No electric signal is required to go through these helical springs..
Figure 2.6. One of the 2 flat gimbals to be used for coupling the GG test bodies (see Figure 3.2). The outer ring of the gimbal is clamped to the PGB tube and the inner one to the coupling arm (in Figure 3.2 the PGB tube is shown in dark green and the coupling arm in light blue). There are 6 wire sectors in between the clamping rings; 3 of them (in alternation) carry electric signals and are insulated at the clamping (on the outer and inner clamping rings). No electric insulation is applied on the thin wires themselves where deformations occur, as it would worsen the mechanical quality.
Drag-free control (with FEEP ion thrusters) of the GG spacecraft reduces the corresponding inertial acceleration on the payload. In order to further reduce its differential effect on the test cylinders due to small differences in their suspensions, the test cylinders are coupled similarly to the two weighs of an ordinary balance (with a vertical instead of horizontal beam in this case) whose arms can be adjusted (by means of piezoceramic actuators) so as to eliminate differential effects. Note that small forces are much easier to balance than large ones. This balancing procedure, which has been tested on the ground prototypeSec. 5 (in a more difficult 1-g environment) to the level currently required for the space experiment, is performed before taking data; electric voltages can be switched off after balancing if inch-worms are used rather than ordinary piezo.
The property of being balanced is a property of the system, not of the particular force acting on it; hence, all other common mode perturbations beside drag (e.g. solar radiation pressure) are also balanced once the main drag effect is balanced. Balancing the drag does not eliminate an EP violation signal it is drag is a differential effect; moreover, drag is variable in time and about 90° out of phase with respect to the signal; the drag free control laws developed during the GG Phase A Study26, Ch. 6 show that memory of the phase difference between the drag and the signal remains after drag compensation. Vibration noise from the FEEP thrusters close to the spin frequency is attenuated by the suspensions of the PGB laboratory enclosing the test bodies.
2.4 Dissipation, Whirl Motions and Their Stabilization
The GG bodies all spin at a frequency much higher than their natural frequencies of oscillation (which are very low because of the very weak suspensions that can be used in absence of weight). This state of rotation is very close to that of ideal, unconstrained, rotors and allows the test cylinders to self-center very precisely (the center of mass of an ideal free rotor would be perfectly centered on the spin axis). However, suspensions are not perfect, which means that, as they undergo deformations at the frequency of spin, they also dissipate energy. The higher the mechanical quality of the suspensions, the smaller the energy losses. Energy dissipation causes the spin rate to decrease, hence also the spin angular momentum will decrease; and since the total angular momentum must be conserved, the suspended bodies will develop slow whirl motions one around the other. Although very slow, whirl motions must be damped. In GG they are damped actively with small capacitance sensors/actuators and appropriate control laws which have been developed, implemented and tested in a numerical simulation of the full GG satellite dynamical system using the software package DCAP of Alenia Spazio (also checked by simulating the GG dynamical system in Matlab). Simulations include drag free control as well. They demonstrate that the system can be fully controlled and that the control does not affect the expected sensitivity of the GG experiment. Indeed, with the measured value of the quality factor of the suspensions (see Figure 2.5), whirl motions of the test cylinders are so slow that they can be damped at time intervals long enough26, Ch. 2.1.5 to allow data taking in between, when active damping is switched off and will therefore produce no disturbance at all on the EP experiment.
Damping of whirl motions in the GG experiment has been the subject of extensive analysis, by the GG Science Team as well as within ESA. Doubts have been expressed and a paper has been published30 arguing that the GG proposed test of the Equivalence Principle would be limited to a sensitivity of 1 part in 1014, which is 3 orders of magnitude worse than the sensitivity expected by the GG Team26. The issue has now been settled31, 26 Ch. 6. The plots of Figure 2.7 are worth showing; although they refer to a simplified 2-body model, they show a very clear comparison between the two approaches. Results from simulations of the complete system can be found in26 Ch. 6. Classical literature is available32,33,34, as well as a brief summary on the specific issue35. The basic physical principles which govern the behavior of weakly coupled fast spinning rotors in space may also be of interest due to the novelty of the subject36. In addition to demonstrating that whirl motions can be accurately damped under realistic flight conditions and therefore the experiment concept is sound, 3 issues claimed in30 as serious difficulties for the GG experiment concept could also be settled, namely: (i) that the pen-shaped small rods which are used to couple the test cylinders are stable; (ii) that memory of the drag phase remains after drag-free control (hence a large angular separation from the signal remains, which is helpful in signal recovery; see Figure 2.8); (iii) that losses in the electrostatic dampers themselves are negligible37..
Figure 2.7 (Taken from31.) Trajectory of the relative motion of the centers of mass of the GG outer spacecraft and the PGB in the plane perpendicular to the spin axis in a 2-body model (coupling constant 0.02N/m, Q=90). The Y axis is pointed to the center of the Earth, hence the largest effect of the residual atmospheric drag, assumed of 5× 10-9N, is a constant displacement along the X axis (of @ 0,08 mm); its second harmonic (assumed 40% of it) appears in this system as a variation at the orbital period (5,700 sec). This is the dashed circle, showing -in both plots- the stationary state that the system would reach if the whirl motion were perfectly damped. The plot on the left is obtained with the control laws of the GG team assuming the following errors: initial bias of 10mm linear and 1° angular; fractional error in spin rate measurements Dws/w s=10-4; offset (by construction and mounting) of 10mm; errors in the capacitors of 0.1mm r.m.s. Whirl oscillations with the natural period of 314 sec (around the points of the dashed circle) and of decreasing amplitude are apparent as the system is brought to its stationary state in 8,000 sec only. Note that at this point the relative distance of the two centers of mass is below 5Å . These results have been obtained independently using DCAP software package (of Alenia Spazio) and Matlab. The plot on the right shows, for the same system, but under much more ideal assumptions (perfect knowledge of spin rate; perfect centering of the rotor; an initial linear bias of 1mm and no angular bias; an error in the sensors/actuators 10 times smaller, i.e. of 10-2
mm) the results obtained by applying the control laws proposed by30. It is apparent that even in a much more favorable situation the same system has been unwittingly transformed into one dominated by very large active forces for which there is in fact no need, as the plot on the left demonstrates. Note that the dissipation has been assumed to be the same in both cases (Q=90), hence failure to stabilize the whirl motion (right hand plot) has to be ascribed only to the control laws implemented in that case. Regarding the plot on the left note that the assumptions for the various error sources are conservative. For instance, small capacitors like those designed for GG can be shown in the laboratory to be sensitive to relative displacements of 10-2mm.It is clear by now that fast rotation and weak mechanical suspensions are the main features of the GG experiment design, distinguishing it from the STEP design. Other advantages of fast rotation beside the modulation of the signal are that a large number of perturbing effects (e.g. due to inhomogeneities of the test bodies, spacecraft mass anomalies, non-uniform thermal expansion, parasitic capacitances, etc.) appear as DC because the entire system is spinning. In addition, as shown in26, Ch. 2.2.2, Earth tidal effects act on the test bodies at twice the spin/signal frequency.
Once whirl motions are damped the relative distance of the test cylinders remains within about 1 Å
(Figure 2.8), undergoing oscillations at their natural differential period (545 sec). The expected signal is about 2 orders of magnitude smaller. Nevertheless, it can be recovered from the data because of its fixed direction (in a non spinning frame it points towards the center of the Earth). Moreover, the numerical simulations reported in Figure 2.8 show that an EP violation signal 100 times smaller than the amplitude of whirl can be recovered even in the presence of a residual drag effect (at a large phase difference from it) about a factor 10 larger than the signal..
Figure 2.8 Relative distance of the GG test masses with their whirl motions actively controlled in a reference frame where the Y axis points to the center of the Earth and the X axis is in the along track direction. The simulation concerns a full scale GG system with realistic error sources according to the GG requirementsSec 2.5. In this case, an EP violation signal was introduced in the system (corresponding to h =10-17, hence yielding about 1/100 Å relative displacement pointing to the center of the Earth) and a larger drag effect along track. Both of them could be recovered from this set of data in spite of the much larger whirl oscillations. A large phase difference between the signal and the residual drag is realistic because numerical simulations of drag free control show that memory of the original phase difference is not lost during drag free control (for the contribution by solar radiation pressure see26, Fig. 2.21). Note that this is a worst case exercise of signal recovery because the mechanical quality of the suspensions of the test bodies assumed in the simulation must be much worse than the measured value (by about 40 times) in order to speed up the onset of the whirl instability during the timespan of the numerical integration (typically requiring 8 hr of CPU time).
2.5 Requirements and Error Budget
The error budget for the GG experiment is given in26, Ch. 2.2. In the worst case assumption of flying the mission close to solar maximum (when air drag perturbation is maximum), assuming the maximum drag value along the satellite orbit and using values already measured in the laboratory for key quantities such as the quality factor and the common mode rejection, the experiment target of testing the Equivalence Principle to 1 part in 1017 can be achieved (see Table 2.1). The situation improves when flying close to solar minimum and with improved values of the quality factor and common mode rejection26, Table 2.2.The requirements which lead to the error budget reported in Table 2.1 are the following (see26, Ch.2.2 for details):
If temperature requirements are fulfilled, 20 days of continuous data taking are allowed before rebalancing the test bodies, and at least 15 days (more if some care is taken in the manufacture of the sensor plates arms) before rebalancing the read-out capacitance bridge. With a mechanical quality factor like the measured one, thermal noise requires an integration time of about 7 days (Table 2.1); for this interval of time the same quality factor allows data taking without active control of whirl instabilities (once damped, there is not enough time for them to grow to values of importance).
Back to GG Proposal to ESA, F2&F3 Competition